이 글은 『미적분학 첫걸음』 4장 3절의 내용입니다. (미적분학 첫걸음 차례 보기)
이 절에서는 연속성과 관련된 정리 세 개를 살펴본다.
이 글에서는 직관적인 증명을 소개한다. 엄밀한 증명을 보고자 한다면 다음 게시글을 확인하기 바란다: 연속함수.
연속함수의 사잇값 정리
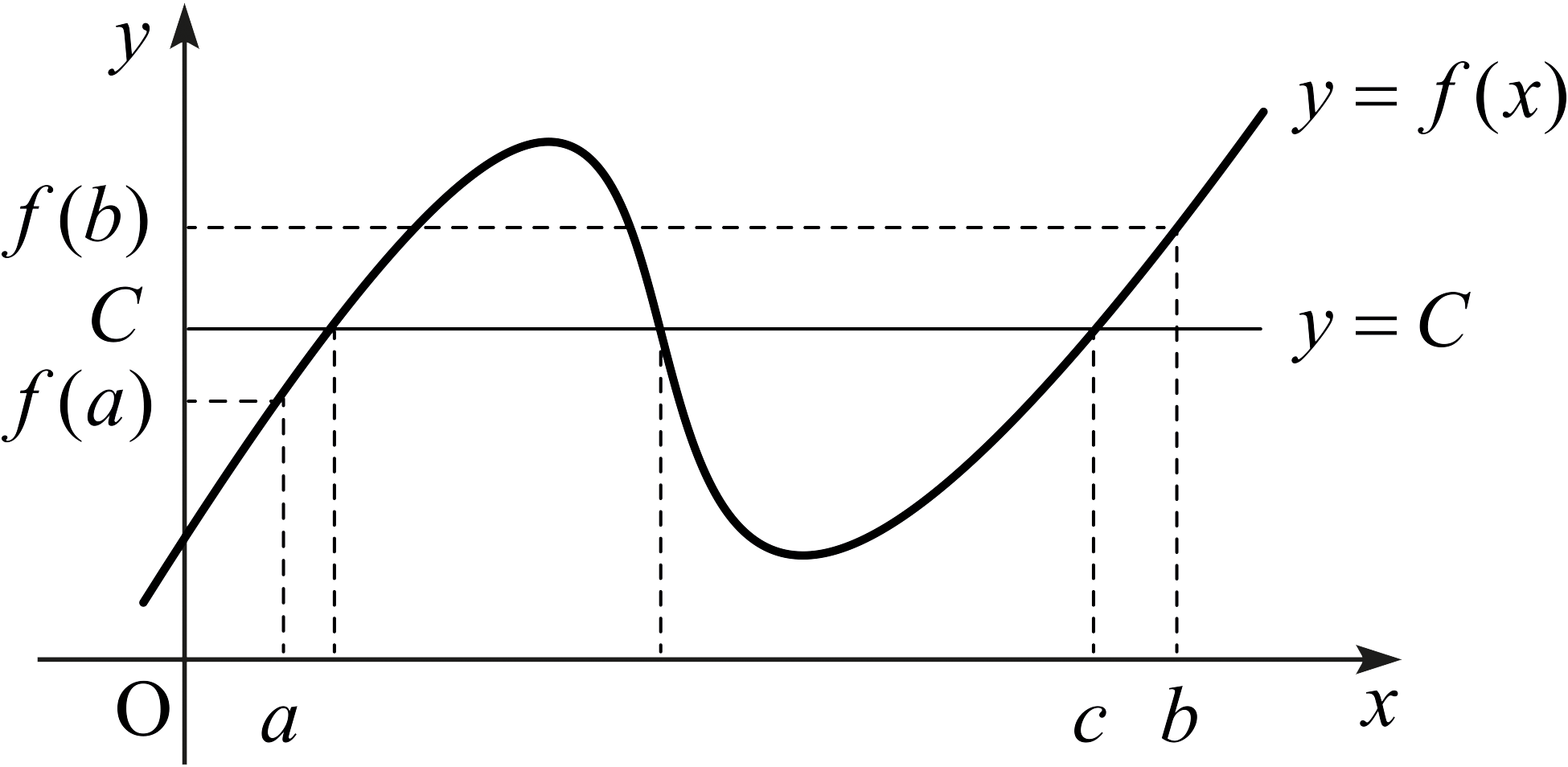
\([a,\,b]\)가 길이가 양수인 구간이고 \(f\)가 \([a,\,b]\)에서 연속인 실숫값 함수라고 하자. 또한 \(f(a) < f(b)\)라고 하자. \(C\)가 \(f(a) < C < f(b)\)인 실수라고 하자. 이제
“\(x > c\)인 모든 \(x\)에 대하여 \(f(x) > C\)”
를 만족시키는 실수 \(c\) 중에서 가장 작은 것을 택하자. 그러면 \(x > c\)일 때마다 \(f(x) \ge C\)이므로 \[\lim_{x\rightarrow c^+} f(x) \ge C\] 가 성립한다. 더욱이 \[\lim_{x\rightarrow c^-} f(x) \le C\] 가 성립한다. 왜냐하면 만약 \(c\)에서 \(f\)의 좌극한 \(f(c^- )\)가 \(C\)보다 더 크다면 “\(x > c\)인 모든 \(x\)에 대하여 \(f(x) > C\)”를 만족시키면서 더 작은 \(c\)가 존재하게 되기 때문이다.
이와 같은 상황은 다음 그림으로 나타낼 수 있다.
이로써 다음 정리를 얻는다.
정리 4.3.1. (연속함수의 사잇값 정리)
\([a,\,b]\)가 길이가 양수인 구간이고 \(f\)가 \([a,\,b]\)에서 연속인 실숫값 함수라고 하자. 그러면 \(f\)는 \([a,\,b]\)에서 \(f(a)\)와 \(f(b)\) 사이에 있는 모든 값을 취한다. 즉 만약 \(f(a) \ne f(b)\)이고 \(C\)가 \(f(a)\)와 \(f(b)\) 사이에 있는 값이면, \(f(c)=C\)를 만족시키는 점 \(c\)가 구간 \((a,\,b)\)에 존재한다.
예제 4.3.1. 방정식 \(x^5 - x^2 - 1 = 0\)이 열린구간 \((0,\,2)\)에서 적어도 하나의 근을 가짐을 보이시오.
풀이. \(f(x) = x^5 - x^2 - 1\)이라고 하자. 그러면 \(f\)는 \(\mathbb{R}\)에서 연속인 함수이다. \(f(0) = -1\)이고 \(f(2) = 27\)이므로 사잇값 정리에 의하여 \(f(c)=0\)을 만족시키는 점 \(c\)가 열린구간 \((0,\,2)\)에 존재한다. 그러한 점 \(c\)가 바로 방정식의 근이다.
연속함수의 최대 최소 정리
\([a,\,b]\)가 길이가 양수인 구간이고 \(f\)가 \([a,\,b]\)에서 연속인 실숫값 함수라고 하자. 이제 \(f\)가 \([a,\,b]\)에서 유계임을 보일 것이다.
결론과는 반대로 \(f\)가 \([a,\,b]\)에서 유계가 아니라고 가정하자. 그러면 \(f\)는 \([a,\,b]\)에서 위로 유계가 아니거나 아래로 유계가 아니다. 일반성을 잃지 않고 \(f\)가 \([a,\,b]\)에서 위로 유계가 아니라고 가정하자.
\(f\)가 \([a,\,b]\)에서 위로 유계가 아니므로, \(n\)이 자연수일 때 \(f(x_n ) > n\)을 만족시키는 점 \(x_n\)이 \([a,\,b]\)에 존재한다. 이와 같이 얻어진 수열 \(\left\{ x_n \right\}\)이 유계인 수열이므로, 볼차노-바이어슈트라스 정리에 의하여 수렴하는 부분수열 \(\left\{ x_{n_k}\right\}\)가 존재한다. \(\left\{ x_{n_k}\right\}\)가 \(c\)에 수렴한다고 하자. \(\left\{ x_{n_k}\right\}\)의 모든 항이 \([a,\,b]\)에 속하므로 \(c\) 또한 \([a,\,b]\)에 속한다. 또한 \(f(x_{n_k}) > n_k\)이므로 \(k\rightarrow\infty\)일 때 \(f(x_{n_k}) \rightarrow \infty\)이다.
한편 \(f\)가 \(c\)에서 연속이므로 \[f(c) = \lim_{x\rightarrow c} f(x) = \lim_{k\rightarrow\infty} f(x_{n_k}) = \infty\] 를 얻는다. 이것은 모순이므로 \(f\)는 \([a,\,b]\)에서 위로 유계이다.
같은 방법으로 \(f\)가 \([a,\,b]\)에서 아래로 유계라는 사실도 증명된다.
정리 4.3.2. (연속함수의 유계성)
\([a,\,b]\)가 길이가 양수인 구간이고 \(f\)가 \([a,\,b]\)에서 연속인 실숫값 함수라고 하자. 그러면 \(f\)가 \([a,\,b]\)에서 유계이다.
같은 조건 아래에서 더 흥미로운 결과를 끌어낼 수 있다.
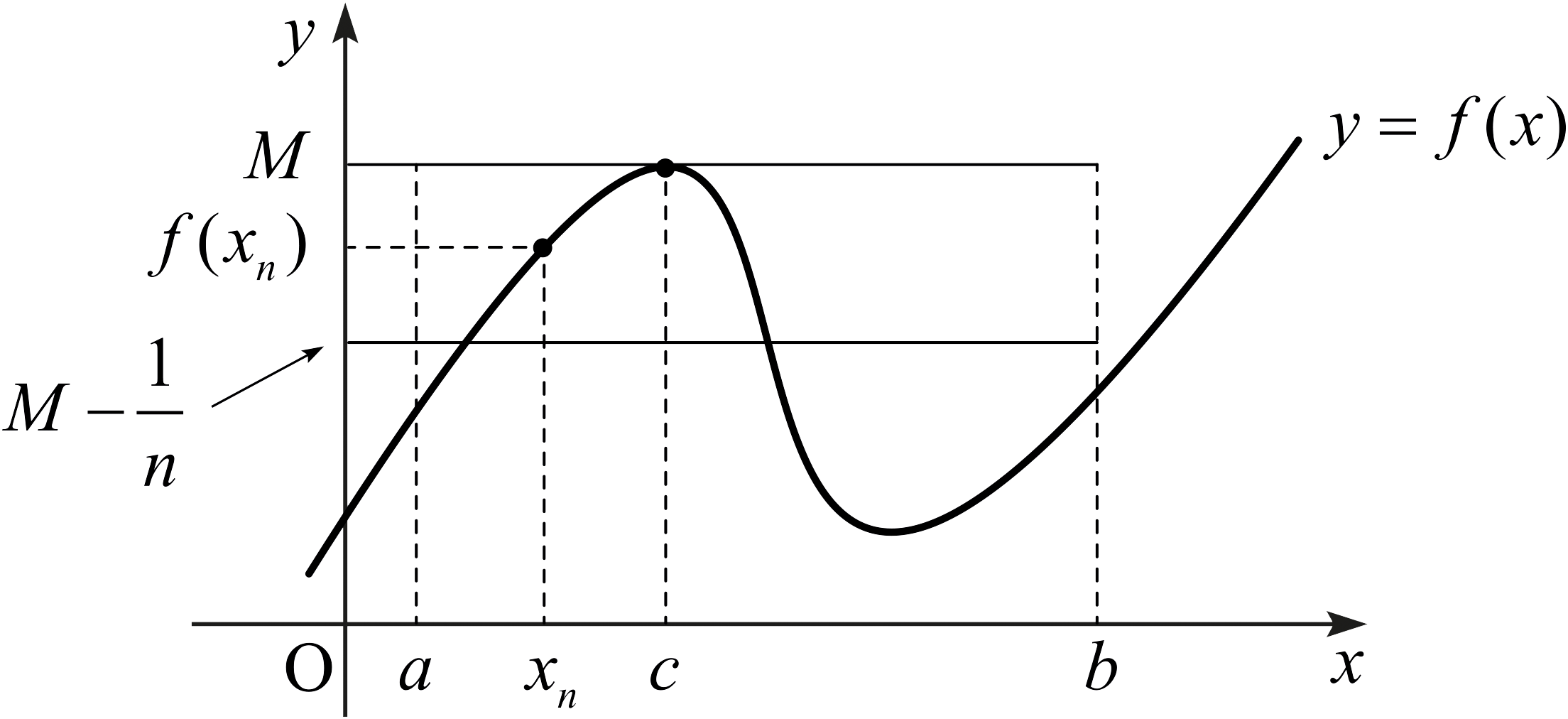
“모든 \(x\in [a,\,b]\)에 대하여 \(f(x) \le M\)”
을 만족시키는 실수 \(M\) 중에서 가장 작은 값을 택하자. 그러면 \(n\)이 자연수일 때 \[f(x_n ) > M - \frac{1}{n}\] 을 만족시키는 점 \(x_n\)이 \([a,\,b]\)에 존재한다.
\(\left\{ x_n \right\}\)이 유계인 수열이므로 볼차노-바이어슈트라스 정리에 의하여 수렴하는 부분수열 \(\left\{ x_{n_k}\right\}\)가 존재한다. \(\left\{ x_{n_k}\right\}\)가 \(c\)에 수렴한다고 하자. 그러면 \(c\in [a,\,b]\)이다. 그런데 \[M \ge f(x_{n_k}) > M - \frac{1}{n_k}\] 이므로 \[\lim_{k\rightarrow\infty} f(x_{n_k}) = M\] 이 성립한다. 더욱이 \(f\)가 \(c\)에서 연속이므로 \[f(c) = \lim_{k\rightarrow\infty} f(x_{n_k}) = M\] 이 성립한다. 그러므로 \(f\)는 \([a,\,b]\)의 점 \(c\)에서 최댓값을 가진다.
같은 방법으로 \(f\)가 \([a,\,b]\)에서 최솟값을 가진다는 사실도 증명된다.
이로써 다음 정리를 증명하였다.
정리 4.3.3. (연속함수의 최대 최소 정리)
\([a,\,b]\)가 길이가 양수인 구간이고 \(f\)가 \([a,\,b]\)에서 연속인 실숫값 함수라고 하자. 그러면 \(f\)가 \([a,\,b]\)에서 최댓값과 최솟값을 가진다.
역함수의 연속성
연속이고 일대일인 함수의 역함수가 연속함수임을 증명해 보자. 미적분학을 처음 공부하는 사람이라면 이 증명을 생략하고 정리의 내용만 확인해도 좋다.
\([a,\,b]\)가 길이가 양수인 구간이고 \(f\)가 \([a,\,b]\)에서 연속인 실숫값 함수라고 하자. 또한 \(f\)가 \([a,\,b]\)에서 순증가한다고 하자. 즉
\(x_1 < x_2 \)일 때 \(f(x_1 ) < f(x_2 )\)
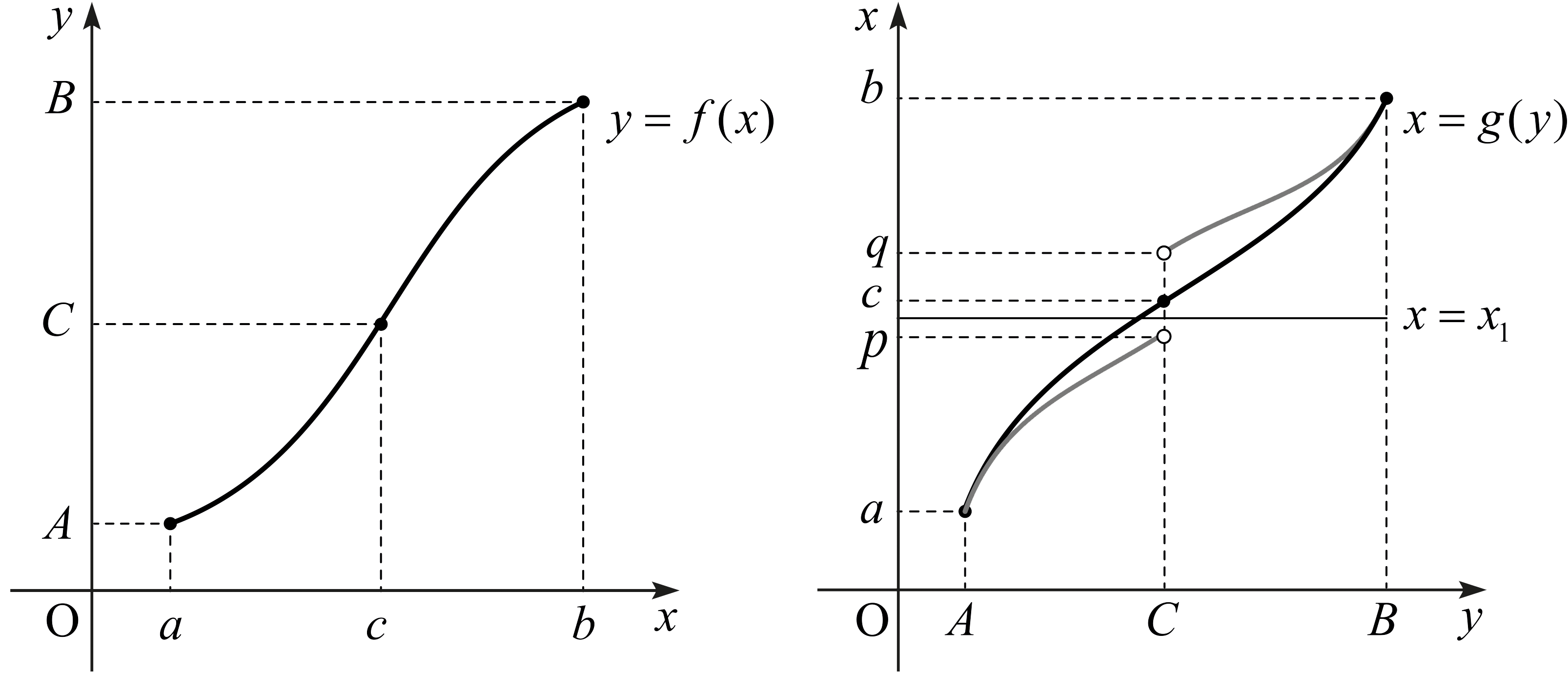
가 성립한다고 하자. 그러면 \(f\)는 \([a,\,b]\)에서 일대일인 함수이다. \(A = f(a),\) \(B = f(b)\)라고 하면 \(f\)가 \([a,\,b]\)로부터 \([A,\,B]\)로의 일대일 함수이므로 그 역함수 \(g = f^{-1}\)가 존재한다.
다음 단계로 넘어가기 전에 \(g\)의 정의역이 \([A,\,B]\)라는 사실을 확인하고 가자. \(C\)가 \([A,\,B]\)에 속하는 점이라고 하자. 그러면 \(f(c)=C\)인 점 \(c\)가 \([a,\,b]\)에 존재한다. 즉 \(g(C) = c\)이다. 그러므로 \(g\)는 \([A,\,B]\)에서 잘 정의된 함수이다.
이제 \(g\)가 \([A,\,B]\)에서 연속임을 보이자. \(C\in [A,\,B]\)라고 하자. 일반성을 잃지 않고 \(A < C < B\)라고 하자. \(g\)가 증가함수이므로 단조수렴 정리에 의하여 \(C\)에서 \(g\)의 좌극한과 우극한이 수렴한다. \(C\)에서 \(g\)의 좌극한을 \(p,\) 우극한을 \(q\)라고 하자. 즉 \[\lim_{y\rightarrow C^-} g(y) = p ,\quad \, \lim_{y\rightarrow C^+} g(y) = q\] 라고 하자. \(g(C) = c\)이고 \(g\)가 순증가하므로 \(p \le c \le q\)이다.
\(p < c\)라고 가정하고, \(p\)와 \(c\) 사이에 있는 값 \(x_1\)을 택하자. 그러면 \(p < x_1 < c\)이고 \(f(p) < f(x_1 ) < f(c)\)이다. 그런데 \(p < x_1\)이므로 \(f(x_1)\)이 \(C\)보다 크다. 왜냐하면, 만약 \(f(x_1 )\)이 \(C\)보다 크지 않다면 \(C\)에서 \(g\)의 좌극한이 \(x_1\) 이상이 되어야 하는데, \(x_1 < c\)이므로 \(f(x_1 )\)이 \(C = f(c)\)보다 커질 수 없기 때문이다. 이것은 모순이므로 \(p=c\)이다.
만약 \(c < p\)라고 가정하면 같은 방법으로 모순에 이른다. 그러므로 \(c = q\)일 수밖에 없다. 즉 \[\lim_{y\rightarrow C^-} g(y) = \lim_{y\rightarrow C^+} g(y) = c = g(C)\] 이다. 그러므로 \(g\)가 \(C\)에서 연속이다.
지금까지 다음 정리를 증명하였다.
정리 4.3.4. (역함수의 연속성)
\([a,\,b]\)가 길이가 양수인 구간이고 \(f\)가 \([a,\,b]\)에서 연속인 실숫값 함수이며 일대일이라고 하자. 또한 \([a,\,b]\)에서 \(f\)의 상(image)을 \(I\)라고 하자. 만약 \(g\)가 \(f\)의 역함수이면 \(g\)는 \(I\)에서 연속이다.
사실 위 정리를 얻기 위해서는 “닫힌구간에서 연속이고 일대일인 함수는 순증가하거나 순감소한다”라는 사실을 증명해야 한다. 어렵지 않으니 직접 증명해 보기 바란다. (사잇값 정리를 사용하여 증명할 수 있다.)
보기 4.3.2. \(x \ge 0\)인 범위에서 \(f(x) = \sqrt{x}\)라고 하자. 그러면 \(f\)는 역함수를 가지며, 역함수는 \(g(x)=x^2 ,\) \(x \ge 0\)으로 주어진다. 그런데 \(g\)가 연속함수이므로 \(f\)도 연속함수이다.
보기 4.3.3. \(f(x) = \sin x\)라고 하자. \(f\)가 닫힌구간 \[I = \left[ - \frac{\pi}{2} ,\, \frac{\pi}{2}\right]\] 에서 연속이고 순증가하므로, 그 역함수 \[g(x) = \sin^{-1} x\] 는 구간 \([-1 ,\,1]\)에서 연속이다.