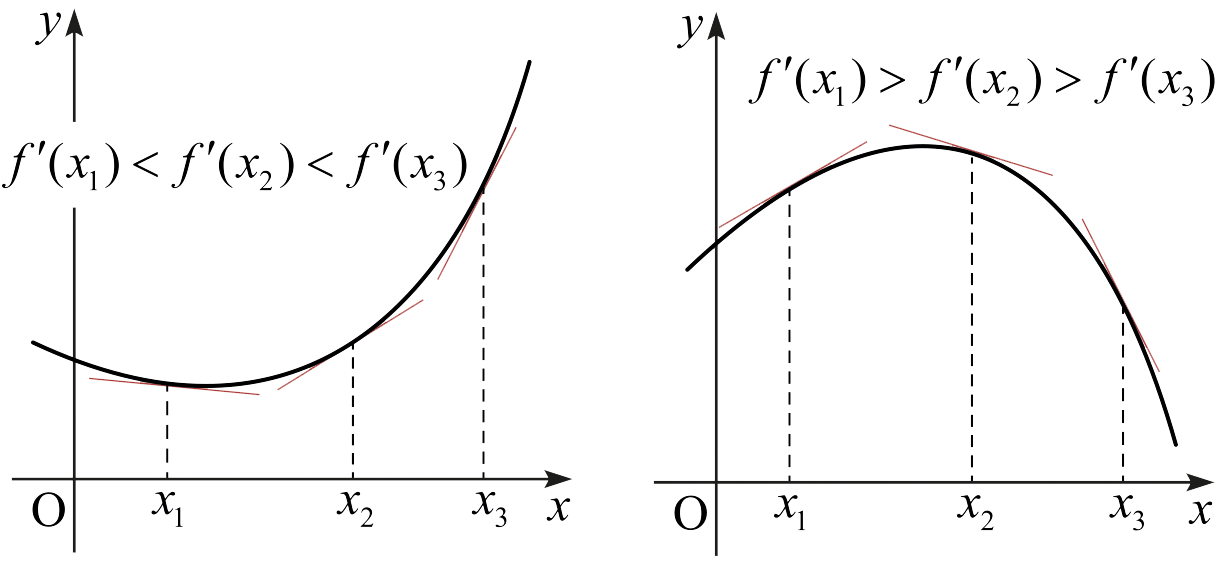이 글은 『미적분학 첫걸음』 5장 3절의 내용입니다. (미적분학 첫걸음 차례 보기)
이 포스트에서는 함수의 극값, 평균값 정리, 함수의 그래프의 볼록성을 살펴봅니다. 이 포스트는 미적분학을 처음 공부하는 사람을 대상으로 하는 내용을 다루며, 정리의 증명을 직관적인 방법으로 설명합니다. 엄밀한 정의와 증명을 보고자 한다면 다음 글을 보기 바랍니다.
함수의 극값
\(I = [a,\,b]\)가 길이가 양수인 구간이며 함수 \(f\)가 구간 \(I\)에서 정의된 실함수이고 \(c\in I\)라고 하자. 이때 다음과 같이 정의한다.
- 만약 임의의 \(x\in I\)에 대하여 \(f(x) \le f(c)\)이면, “\(f\)가 \(c\)에서 최댓값을 가진다”라고 말하고, \(f(c)\)를 최댓값(maximum value)이라고 부른다.
- 만약 임의의 \(x\in I\)에 대하여 \(f(x) \ge f(c)\)이면, “\(f\)가 \(c\)에서 최솟값을 가진다”라고 말하고, \(f(c)\)를 최솟값(minimum value)이라고 부른다.
- 만약 \(c\)를 원소로 갖는 열린구간 \(J\)가 존재하여, \(I\cap J\)에서 \(f\)의 최댓값이 \(f(c)\)가 되면, “\(f\)가 \(c\)에서 극댓값을 가진다”라고 말한다. (local maximum)
- 만약 \(c\)를 원소로 갖는 열린구간 \(J\)가 존재하여, \(I\cap J\)에서 \(f\)의 최솟값이 \(f(c)\)가 되면, “\(f\)가 \(c\)에서 극솟값을 가진다”라고 말한다. (local minimum)
- 극댓값과 극솟값을 통틀어 극값(local extremum)이라고 부른다.
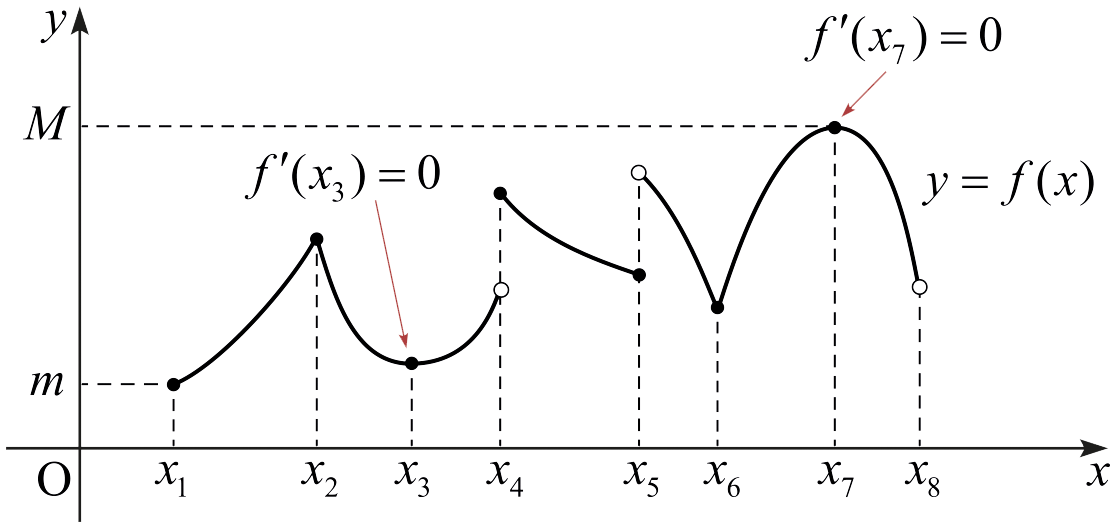
보기 5.3.1. 함수 \(y=f(x)\)의 그래프가 다음 그림과 같다고 하자.
함수 \(f\)가 극댓값을 갖는 점은 \(x_2 ,\) \(x_4 ,\) \(x_7\)이며, \(f\)가 극솟값을 갖는 점은 \(x_1 ,\) \(x_3 ,\) \(x_5 ,\) \(x_6\)이다. \(f\)는 \(x_7\)에서 최댓값 \(M\)을 가지며, \(x_1\)에서 최솟값 \(m\)을 가진다. \(x_8\)에서 \(f\)는 극값을 갖지 않는다.
구간에서 정의된 함수 \(f\)가 미분 가능한 경우, 미분계수를 이용하여 \(f\)가 극값을 가질 만한 점을 찾을 수 있다.
\(f\)가 구간 \([a,\,b]\)에서 정의되어 있고 \(c\in (a,\,b)\)라고 하자. 또한 \(f\)가 \(c\)에서 극댓값을 가지며, \(c\)에서 미분 가능하다고 하자. 그러면 \(c\)에서 \(f\)의 좌미분계수는 \[f_l ' (c) = \lim_{\Delta x \rightarrow 0^-} \frac{f(c+\Delta x) - f(c)}{\Delta x} \ge 0\] 이고, \(c\)에서 \(f\)의 우미분계수는 \[f_r ' (c) = \lim_{\Delta x \rightarrow 0^+} \frac{f(c+\Delta x) - f(c)}{\Delta x} \le 0\] 이다. 그런데 \(f\)가 \(c\)에서 미분 가능하므로 \[f ' (c) = f_l ' (c) = f_r ' (c)\] 이다. 그러므로 \(f ' (c) = 0\)이다.
\(f\)가 \(c\)에서 극솟값을 갖는 경우도 같은 방법으로 \(f ' (c) =0\)이라는 결론을 얻는다.
지금까지 다음 정리를 증명하였다.
정리 5.3.1. 함수 \(f\)가 \(c\)를 원소로 갖는 한 열린구간에서 정의되었다고 하자. 만약 \(f\)가 \(c\)에서 극값을 갖고 \(c\)에서 미분 가능하면, \(f ' (c) = 0\)이다.
보기 5.3.2. \(f(x) =x^3 +x\)라고 하자. \(f ' (x) = 3x^2 +1\)이므로 임의의 \(x\)에 대하여 \(f ' (x) > 0\)이다. 그러므로 \(f\)는 어느 점에서도 극값을 갖지 않는다.
정리 5.3.1의 역은 성립하지 않을 수 있다. 다음 예를 보자.
보기 5.3.3. \(g(x)=x^3\)이라고 하자. 그러면 \(g ' (x) = 3x^2\)이므로, \(g ' (x)=0\)인 점은 \(x=0\) 뿐이다. 그런데 \(x_1 < x_2\)일 때 \( (x_1 )^3 < (x_2)^3 \)이므로 \(g\)는 모든 곳에서 순증가한다. 즉 \(g\)는 \(0\)에서 극값을 갖지 않는다.
평균값 정리
실함수 \(f\)가 \([a,\,b]\)에서 정의되어 있고 이 구간에서 연속이라고 하자. 또한 \(f\)가 열린구간 \((a,\,b)\)에서 미분 가능하고 \(f(a) = f(b)\)가 성립한다고 하자.
만약 \(f\)가 \([a,\,b]\)에서 상수함수라면 \((a,\,b)\)의 모든 점 \(c\)에서 \(f ' (c)=0\)이다.
만약 \(f\)가 \([a,\,b]\)에서 상수함수가 아니라면 \(f\)가 극값을 갖는 점 \(c\)가 \((a,\,b)\)에 존재한다. 그러면 정리 5.3.1에 의하여 \(f ' (c)=0\)이다.
지금까지 다음 정리를 증명하였다.
정리 5.3.2. (롤의 정리; Rolle's Theorem)
실함수 \(f\)가 길이가 양수인 닫힌구간 \([a,\,b]\)에서 정의되어 있고 이 구간에서 연속이라고 하자. 또한 \(f\)가 열린구간 \((a,\,b)\)에서 미분 가능하고 \(f(a) = f(b)\)가 성립한다고 하자. 그러면 \(f ' (c)=0\)인 점 \(c\)가 열린구간 \((a,\,b)\)에 존재한다.
위 정리를 더 일반적인 경우로 확장할 수 있다. 정리 5.3.2에서와 같은 조건이 주어졌다고 하자. 단 \(f(a) = f(b)\)라는 조건은 빼자. 구간 \([a,\,b]\)에서 함수 \(g\)와 \(h\)를 \[g(x) = \frac{f(b)-f(a)}{b-a} (x-a) +f(a)\] 그리고 \[h(x) = f(x)-g(x)\] 라고 정의하자. 그러면 \(h\)는 \([a,\,b]\)에서 연속이고 \((a,\,b)\)에서 미분 가능하며 \(h(a)=h(b)\)가 성립한다. 따라서 롤의 정리에 의하여 \(h ' (c)=0\)인 점 \(c\)가 \((a,\,b)\)에 존재한다. 그런데 \[h ' (c) = f ' (c) - g ' (c) = f ' (c) - \frac{f(b) -f(a)}{b-a}\] 이므로 \[\frac{f(b)-f(a)}{b-a} = f ' (c)\] 를 얻는다. 지금까지 다음 정리를 증명하였다.
정리 5.3.3. (평균값 정리; The Mean Value Theorem)
실함수 \(f\)가 길이가 양수인 닫힌구간 \([a,\,b]\)에서 정의되었다고 하자. 만약 \(f\)가 닫힌구간 \([a,\,b]\)에서 연속이고 열린구간 \((a,\,b)\)에서 미분 가능하면, \[\frac{f(b)-f(a)}{b-a} = f ' (c)\] 를 만족시키는 점 \(c\)가 열린구간 \((a,\,b)\)에 존재한다.
평균값 정리는 미분계수를 이용하여 함수의 성질을 밝히는 데에 자주 사용된다. 이어지는 내용을 살펴보자.
함수의 증가와 감소
\(I\)가 길이가 양수인 구간이고 \(f\)가 \(I\)에서 정의된 실함수라고 하자. 또한 \(f\)가 \(I\)에서 미분 가능하다고 하자. 만약 \(x_1\)과 \(x_2\)가 \(I\)에 속한 점이고 \(x_1 < x_2\)이면, 평균값 정리에 의하여 \[\frac{f(x_2 ) - f(x_1 )}{x_2 - x_1} = f ' (c)\] 를 만족시키는 점 \(c\)가 \(x_1\)과 \(x_2\) 사이에 존재한다. 즉 \[f(x_2 ) - f(x_1 ) = f ' (c) (x_2 - x_1 )\] 이다. 이 식으로부터 \(f(x_2 ) - f(x_1 )\)의 부호와 \(f ' (c)\)의 부호가 일치함을 알 수 있다. 따라서 다음 결론을 얻는다.
정리 5.3.4. (함수의 증감에 대한 일계도함수 판정법)
\(I\)가 길이가 양수인 구간이고 \(f\)가 \(I\)에서 정의된 실함수라고 하자. 또한 \(f\)가 \(I\)에서 미분 가능하다고 하자.
- 만약 \(I\)의 모든 점 \(x\)에서 \(f ' (x) > 0\)이면, \(f\)는 \(I\)에서 순증가한다.
- 만약 \(I\)의 모든 점 \(x\)에서 \(f ' (x) < 0\)이면, \(f\)는 \(I\)에서 순감소한다.
- 만약 \(I\)의 모든 점 \(x\)에서 \(f ' (x) = 0\)이면, \(f\)는 \(I\)에서 상수함수이다.
만약 함수 \(f\)가 점 \(c\)를 원소로 갖는 한 열린구간에서 미분 가능하고 \(f ' (c)=0\)이라고 하자. 그러면 \(c\) 근처에서 함수의 그래프의 모양은 다음 네 가지 경우가 있다.
따라서 \(c\) 근처에서 \(f ' \)의 부호의 변화를 살핌으로써 \(f\)가 \(c\)에서 극값을 갖는지 여부를 조사할 수 있다. 더욱이 \(c\)에서 \(f\)가 미분 가능하지 않고 \(c\) 근처에서 \(f\)가 미분 가능하기만 하여도 같은 방법으로 \(f ' \)의 부호의 변화를 살핌으로써 \(f\)가 \(c\)에서 극값을 갖는지 여부를 조사할 수 있다. 이 사실을 정리하면 다음과 같다.
정리 5.3.5. (함수의 극값에 대한 일계도함수 판정법)
실함수 \(f\)가 점 \(c\)를 원소로 갖는 한 열린구간 \(I\)에서 정의되었다고 하자. 그리고 \(f\)가 \(I\)에서 \(c\)를 제외한 모든 점에서 미분 가능하다고 하자. (\(c\)에서 \(f\)는 미분 가능할 수도 있고 아닐 수도 있다.)
- \(x\)의 값이 \(c\)의 왼쪽에서 오른쪽으로 지날 때 \(f ' (x)\)의 부호가 음에서 양으로 바뀌면 \(f\)가 \(c\)에서 극솟값을 가진다.
- \(x\)의 값이 \(c\)의 왼쪽에서 오른쪽으로 지날 때 \(f ' (x)\)의 부호가 양에서 음으로 바뀌면 \(f\)가 \(c\)에서 극댓값을 가진다.
- \(x\)의 값이 \(c\)의 왼쪽에서 오른쪽으로 지날 때 \(f ' (x)\)의 부호가 바뀌지 않으면 \(f\)가 \(c\)에서 극값을 갖지 않는다.
실함수 \(f\)가 구간 \(I\)에서 정의되어 있고 \(c\)가 \(I\)의 점이라고 하자. 만약 \(f ' (c)=0\)이거나 \(f\)가 \(c\)에서 미분 불가능하면, \(c\)를 \(f\)의 임계점(critical point)이라고 부른다. (임계점은 그래프 위의 점이 아니라 정의역의 점이라는 사실을 주의하자.)
정리 5.3.5에 의하면 함수 \(f\)가 구간 \(I\)에서 정의되어 있을 때 \(f\)가 극값을 갖는 점은 임계점과 \(I\)의 양 끝점 뿐이다. 이 사실을 이용하여 함수가 극값을 갖는 점을 조사할 수 있다. 다음 예를 보자.
보기 5.3.4. 함수 \(f\)가 구간 \([1,\,5]\)에서 \[f(x) = -x^2 +4x+3\] 으로 정의되었다고 하자. 그러면 \(f\)는 \([1,\,5]\)에서 미분 가능하고 \[f ' (x) = -2x+4\] 이다. 따라서 \(f ' (x)=0\)인 점은 \(x=2\) 뿐이다. 이 점에서 함숫값은 \[f(2)=7\]이다.
다음으로 구간의 끝점에서 함숫값은 \[f(1) = 6 ,\quad f(5)=-2\]이다.
그러므로 \([1,\,5]\)에서 \(f\)는 최댓값 \(f(2)=7\)을 가지며, 최솟값 \(f(5)=-2\)를 가진다.
그래프의 볼록성
실함수 \(f\)가 길이가 양수인 구간 \(I\)에서 정의되었고, 이 구간에서 연속이라고 하자. 만약 이 함수의 그래프 위의 임의의 두 점을 이었을 때 그 선분이 그래프의 아래쪽에 놓이지 않으면 “\(I\)에서 \(f\)의 그래프가 아래쪽으로 볼록하다”라고 말한다. 만약 이 함수의 그래프 위의 임의의 두 점을 이었을 때 그 선분이 그래프의 위쪽에 놓이지 않으면 “\(I\)에서 \(f\)의 그래프가 위쪽으로 볼록하다”라고 말한다.
만약 함수 \(f\)가 \(I\)에서 미분 가능하다면 \(f\)의 도함수를 이용하여 \(f\)의 그래프의 볼록성을 다음과 같이 판별할 수 있다.
- 도함수 \(f ' \)가 \(I\)에서 증가하면 \(I\)에서 \(f\)의 그래프가 아래쪽으로 볼록하다. (concave upward)
- 도함수 \(f ' \)가 \(I\)에서 감소하면 \(I\)에서 \(f\)의 그래프가 위쪽으로 볼록하다. (concave downward)
이 상황은 다음과 같이 그래프로 나타낼 수 있다.
만약 \(f\)가 \(I\)에서 두 번 미분 가능하다면, \(f\)의 이계도함수의 함숫값의 부호를 사용하여 \(f\)의 그래프의 볼록성을 판정할 수 있다. 다음 정리를 보자.
정리 5.3.6. (그래프의 볼록성에 대한 이계도함수 판정법)
실함수 \(f\)가 길이가 양수인 구간 \(I\)에서 정의되었다고 하자. 그리고 \(I\)에서 \(f\)가 두 번 미분 가능하다고 하자.
- 만약 \(I\)의 모든 점 \(x\)에서 \(f ' ' (x) > 0\)이면, \(I\)에서 \(f\)의 그래프가 아래쪽으로 볼록하다.
- 만약 \(I\)의 모든 점 \(x\)에서 \(f ' ' (x) < 0\)이면, \(I\)에서 \(f\)의 그래프가 위쪽으로 볼록하다.
보기 5.3.5. 함수 \(f\)가 이차함수라고 하자. 즉 \[f(x) = ax^2 + bx + c , \quad a \ne 0\] 이라고 하자. \(f ' ' (x)= a\)이므로 그래프 \(y=f(x)\)의 볼록성은 \(a\)의 부호에 의하여 결정된다.
만약 \(a > 0\)이면 \(f\)의 그래프는 아래쪽으로 볼록하며, \(a < 0\)이면 \(f\)의 그래프는 위쪽으로 볼록하다.
함수 \(f\)의 그래프가 점 \((c ,\, f(c))\)에서 접선을 가지고, 그 점에서 그래프가 볼록한 방향이 바뀌면, 점 \((c,\,f(c))\)를 \(f\)의 그래프의 변곡점(point of inflection)이라고 부른다.
정리 5.3.7. (변곡점에서의 이계미분계수)
점 \((c,\,f(c))\)가 함수 \(f\)의 그래프의 변곡점이면, \(f ' ' (c) = 0\)이거나 또는 \(f ' ' (c)\)가 존재하지 않는다.
보기 5.3.6. 다음과 같이 주어진 함수 \(g : \mathbb{R} \rightarrow \mathbb{R}\)를 살펴보자. \[g(x) = x^3 + x^2 + x\] 함수 \(g\)를 미분하면 \[g ' (x) = 3x^2 +2x +1\] 그리고 \[g ' ' (x) = 6x + 2\] 이다. 따라서 \(y=g(x)\)의 그래프는 \(x < - \frac{1}{3}\)인 범위에서 아래쪽으로 볼록하고, \(x > - \frac{1}{3}\)인 범위에서 위쪽으로 볼록하다. 점 \(\left( -\frac{1}{3} ,\, -\frac{7}{27} \right)\)은 함수 \(g\)의 그래프의 변곡점이다.
정리 5.3.1에서 함수 \(f\)가 미분 가능하고 점 \(c\)에서 극값을 가지면 \(f ' (c)=0\)임을 살펴보았다. 또한 정리 5.3.5에서 도함수 \(f ' \)의 부호의 변화를 관찰함으로써 \(f\)가 \(c\)에서 극값을 갖는지 여부를 판단할 수 있었다. 만약 \(f\)가 두 번 미분 가능하면 이계도함수 \(f ' ' \)의 부호를 관찰함으로써 \(c\)에서 \(f\)가 극값을 갖는지 여부를 판단할 수 있다. 다음 정리를 보자.
정리 5.3.8. (함수의 극값에 대한 이계도함수 판정법)
\(I\)가 길이가 양수인 구간이고 \(f\)가 \(I\)에서 정의된 함수이며, \(f\)가 \(I\)에서 연속인 이계도함수를 가진다고 하자. \(c\)가 \(I\)의 안쪽에 잇는 점이고 \(f ' (c) = 0\)이라고 하자.
- 만약 \(f ' ' (c) < 0\)이면, \(f\)는 \(x=c\)에서 극댓값을 가진다.
- 만약 \(f ' ' (c) > 0\)이면, \(f\)는 \(x=c\)에서 극솟값을 가진다.
- 만약 \(f ' ' (c) = 0\)이면, 이 판정법을 사용하여 \(f\)가 \(x=c\)에서 극값을 갖는지 여부를 판정할 수 없다.
보기 5.3.7. 다음과 같이 주어진 다항함수 \(h\)를 살펴보자. \[h(x) = x^3 - 3x.\] 이 함수를 미분하면 \[h ' (x) = 3x^2 - 3\] 그리고 \[h ' ' (x) = 6x\] 이다. 방정식 \(h ' (x) = 0\)을 풀면 \(x=-1\) 또는 \(x=1\)이다. 그런데 \[h ' ' (-1) = -6 < 0 ,\quad h ' ' (1) = 6 > 0\] 이므로, \(h\)는 \(-1\)에서 극댓값 \(2\)를 가지며, \(1\)에서 극솟값 \(-2\)를 가진다.
보기 5.3.8. 다항함수 \(f\)가 \[f(x)= x^4 + 4x^3\] 으로 주어졌다고 하자. 미분을 이용하여 이 함수의 그래프의 개형을 조사해 보자.
먼저 \(f(x)\)의 식을 인수분해하면 \[f(x) = x^3 (x+4)\] 이다. 다음으로 \(f\)를 미분하면 다음과 같다. \[\begin{align} f ' (x) &= 4x^3 + 12x^2 = 4x^2 (x+3) , \\[6pt] f ' ' (x) &= 12x^2 + 24x = 12x(x+2) . \end{align}\] 두 방정식 \(f ' (x) =0,\) \(f ' ' (x) =0\)의 근을 구하고, 이 근을 기준으로 표를 만들면 다음과 같다.
이 표를 바탕으로 함수 \(y=f(x)\)의 그래프를 그리면 다음과 같다.
표와 그래프를 통해 알 수 있는 \(f\)의 성질은 다음과 같다.
- 함수 \(f\)의 임계점은 \(-3\)과 \(0\)이다.
- \(f\)는 \(-3\)에서 최솟값 \(-27\)을 가진다.
- \(-3\) 이외의 점에서 \(f\)는 극값을 갖지 않는다. 따라서 \(f\)는 최댓값을 갖지 않는다.
- \(f\)의 그래프의 변곡점은 \((-2,\,-16)\)과 \((0,\,0)\)이다.
- 앞의 글 : 미분 공식
- 다음 글 : 기본 초월함수의 미분