삼각함수

by I Seul Bee

이 글은 『미적분학 첫걸음』 0장 6절의 내용입니다.  (미적분학 첫걸음 차례 보기)

호도법

그림과 같이 반지름의 길이가 \(1\)인 원을 생각하자.

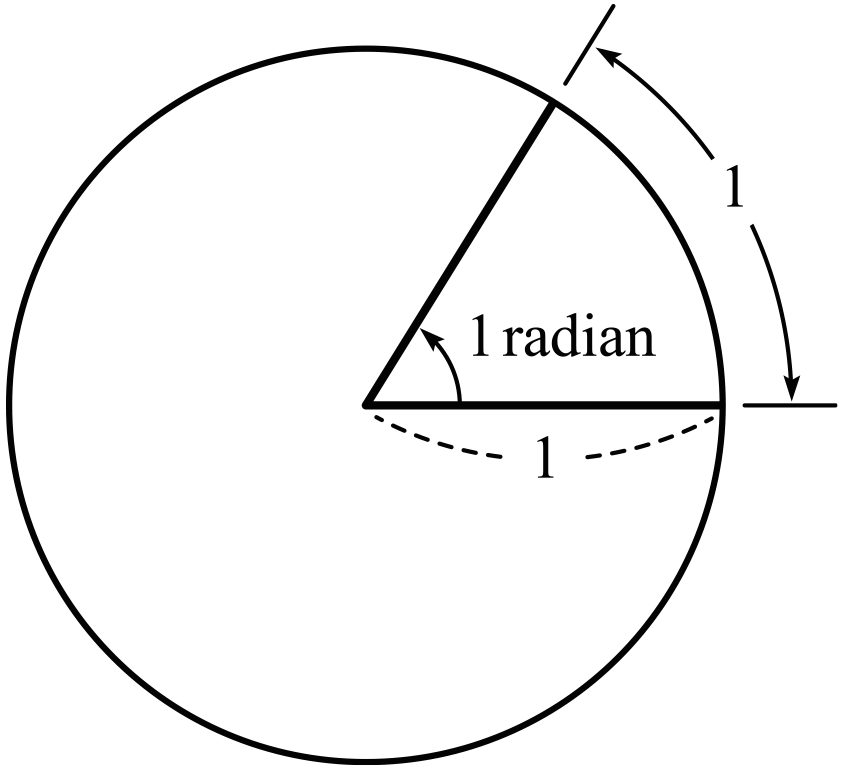
호의 길이가 \(1\)인 부채꼴의 중심각의 크기를 \(\boldsymbol{1}\)라디안(radian)으로 정의한다. 반지름의 길이가 \(1\)인 원의 둘레의 길이가 \(2\pi\)이므로 \[180^\circ = \pi \,\text{radians}\] 이다. 이와 같이 라디안을 단위로 각의 크기를 나타내는 방법을 호도법(circular measure)이라고 부른다.

호도법으로 각의 크기를 나타낼 때 단위 ‘라디안’을 생략하는 경우가 많다. 그러므로 각의 크기를 단위 없이 나타내면 별다른 언급이 없는 한 단위가 ‘라디안’인 것으로 약속한다.

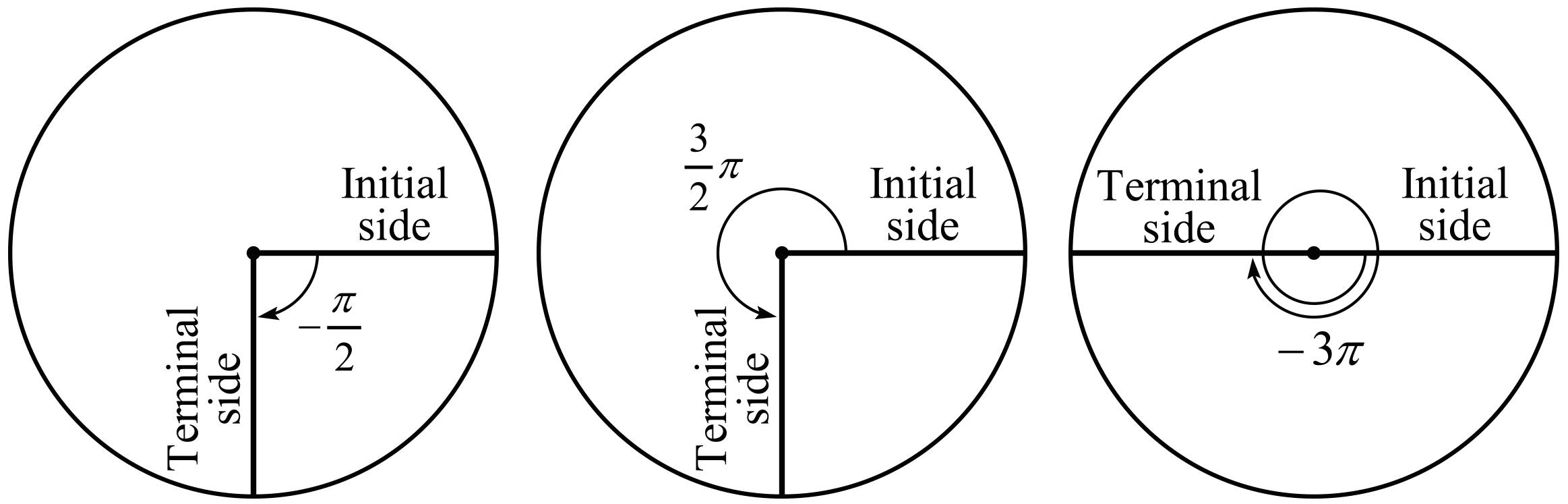
회전 방향에 따라 각의 크기를 양수와 음수로 나타내면 편리하다. 즉 반시계방향으로 회전한 정도를 각으로 표현할 땐 각의 크기를 양수로 나타내고 시계방향으로 회전한 정도를 각으로 표현할 땐 각의 크기를 음수로 나타낸다. 한 바퀴를 초과하는 회전을 각으로 나타낼 땐 절댓값이 \(2\pi\)보다 큰 값을 사용한다. 아래 그림은 다양한 각의 크기를 나타낸 것이다.

삼각함수의 정의

실수 \(\theta\)가 주어졌다고 하자. 그리고 좌표평면에서 원점을 중심으로 \(x\)축의 양의 방향에서 출발하여 \(\theta\)만큼 회전한 반직선 위에 놓인 점 \(\mathrm{P}\)를 생각하자. (여기서 점 \(\mathrm{P}\)는 원점이 아닌 점을 생각한다.)

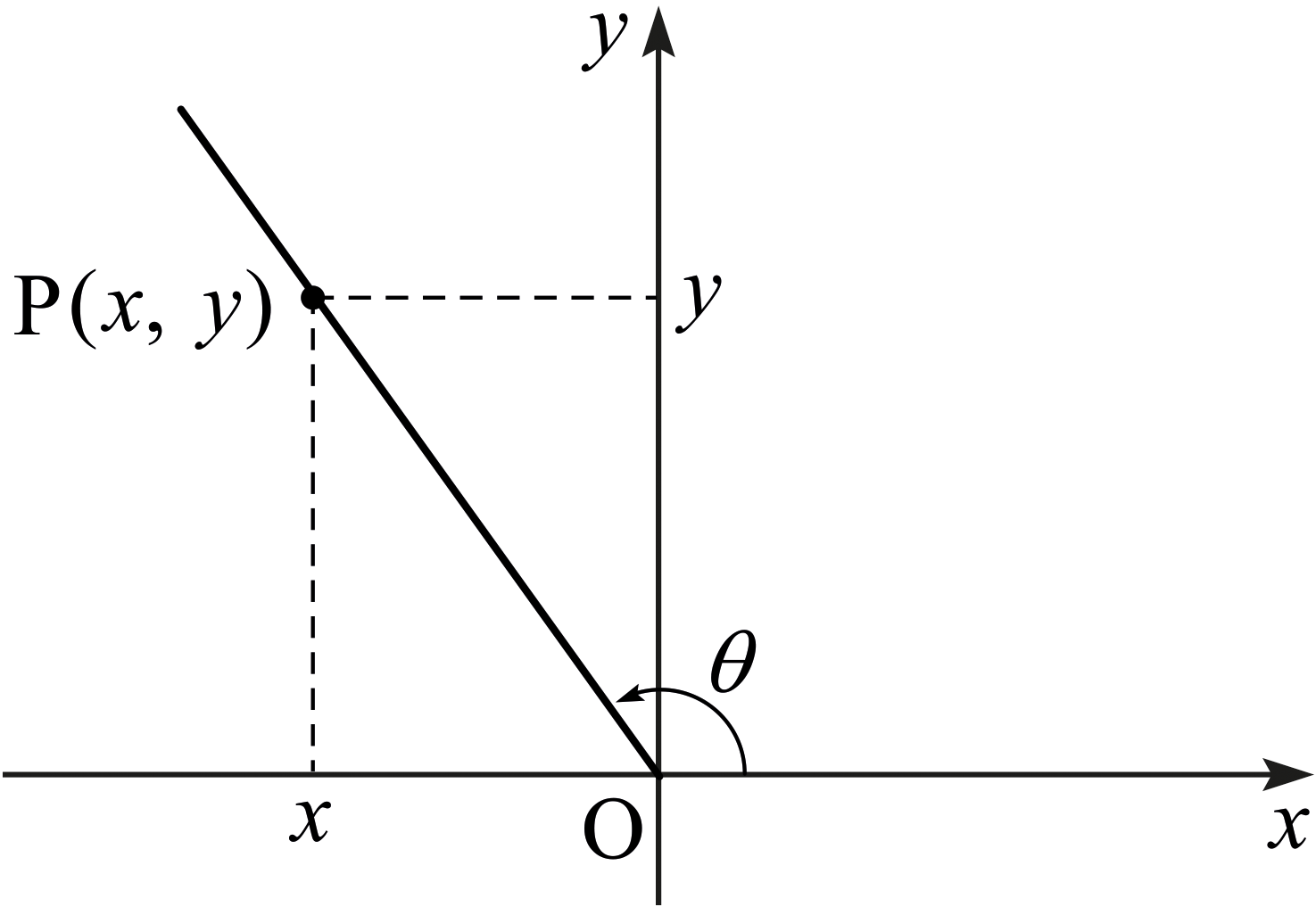
그림과 같이 점 \(\mathrm{P}\)의 좌표를 \(\mathrm{P}(x,\,y)\)라고 하자. 그리고 선분 \(\mathrm{OP}\)의 길이를 \(r\)라고 하자. 이때 \(\theta\)의 사인(sine)과 코사인(cosine)을 다음과 같이 정의한다. \[\sin\theta = \frac{y}{r} ,\quad \cos\theta = \frac{x}{y} .\] 다른 삼각함수는 다음과 같이 정의한다. \[\begin{gather} \tan\theta = \frac{\sin\theta}{\cos\theta} ,\quad \sec\theta = \frac{1}{\cos\theta} ,\\[5pt] \operatorname{cosec}\theta = \frac{1}{\sin\theta} ,\quad \cot\theta = \frac{\cos\theta}{\sin\theta}. \end{gather}\] 각 삼각함수는 당연히 분수식의 분모가 \(0\)이 되도록 하지 않는 \(\theta\)에 대해서만 정의된다.

유용한 공식

삼각함수의 거듭제곱을 나타낼 땐 관습적으로 지수를 함수의 옆에 붙여 쓴다. 예컨대 다음과 같이 쓴다. \[\sin^2 \theta = (\sin \theta )^2 ,\,\, \cos^3 \theta = (\cos\theta )^3 ,\,\, \cdots\] 삼각함수의 정의를 이용하면 다음 등식을 유도할 수 있다.

  • \( \sin^2 \theta + \cos^2 \theta = 1 . \)
  • \( \sin(\theta + 2\pi ) = \sin\theta ,\,\, \cos(\theta + 2\pi ) = \cos\theta . \)
  • \( \sin(-\theta ) = - \sin\theta ,\,\, \cos(-\theta ) = \cos\theta . \)
  • \( \sin\left(\frac{\pi}{2} - \theta \right) = \cos\theta ,\,\, \cos\left(\frac{\pi}{2} - \theta\right) = \sin\theta . \)

첫째 등식은 피타고라스 정리로부터 얻어진다: \[\sin^2 \theta + \cos^2 \theta = \frac{y^2}{r^2} + \frac{x^2}{r^2} = \frac{x^2 +y^2}{r^2} = \frac{r^2}{r^2} = 1.\] 두 번째 등식은 삼각함수가 주기함수임을 나타낸다.

이제 자주 사용되는 공식 세 가지를 살펴보자.

정리 0.6.1. (코사인 법칙)

삼각형 \(\mathrm{ABC}\)에서 다음이 성립한다.

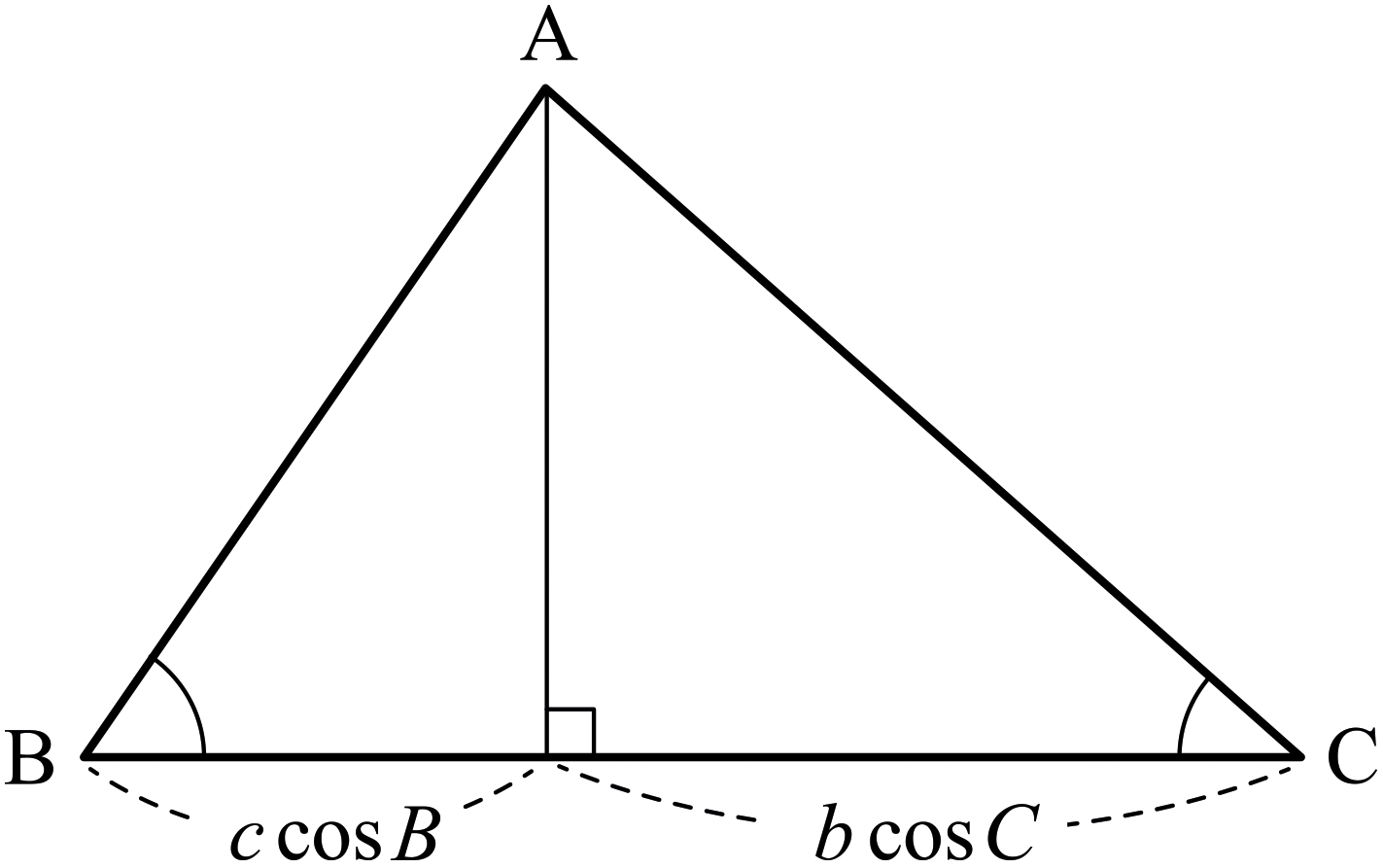
(ⅰ) 제 1 코사인 법칙: \[\begin{align} a &= b \cos C + c \cos B , \\[6pt] b &= a \cos C + c \cos A , \\[6pt] c &= a \cos B + b \cos A. \end{align}\] (ⅱ) 제 2 코사인 법칙: \[\begin{align} a^2 &= b^2 + c^2 - 2bc \cos A , \\[6pt] b^2 &= a^2 + c^2 - 2ac \cos B , \\[6pt] c^2 &= a^2 + b^2 - 2ab \cos C . \end{align}\] 여기서 \(A,\) \(B,\) \(C\)는 각각 꼭짓점 \(\mathrm{A},\) \(\mathrm{B},\) \(\mathrm{C}\)의 내각이며, \(a,\) \(b,\) \(c\)는 각각 꼭짓점 \(\mathrm{A},\) \(\mathrm{B},\) \(\mathrm{C}\)의 대변의 길이이다.

증명.

제 1 코사인 법칙은 다음 그림을 이용하면 쉽게 증명된다.

제 2 코사인 법칙은 제 1 코사인 법칙을 결합하면 증명된다. 즉 제 1 코사인 법칙의 세 등식에 순서대로 양변에 \(a,\) \(b,\) \(c\)를 곱하면 다음을 얻는다. \[\begin{align} a^2 &= ab \cos C + ac \cos B , \\[6pt] b^2 &= ab \cos C + bc \cos C , \\[6pt] c^2 &= ac \cos B + bc \cos A . \end{align}\] 이 식을 결합하면 제 2 코사인 법칙의 세 등식을 얻는다.

정리 0.6.2. (사인 법칙)

반지름의 길이가 \(R\)인 원 \(\mathrm{O}\) 위에 서로 다른 세 점 \(\mathrm{A},\) \(\mathrm{B},\) \(\mathrm{C}\)가 있다고 하자. 이때 삼각형 \(\mathrm{ABC}\)에 대하여 다음이 성립한다. \[\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C} = 2R.\]

증명.

다음 그림을 살펴보자.

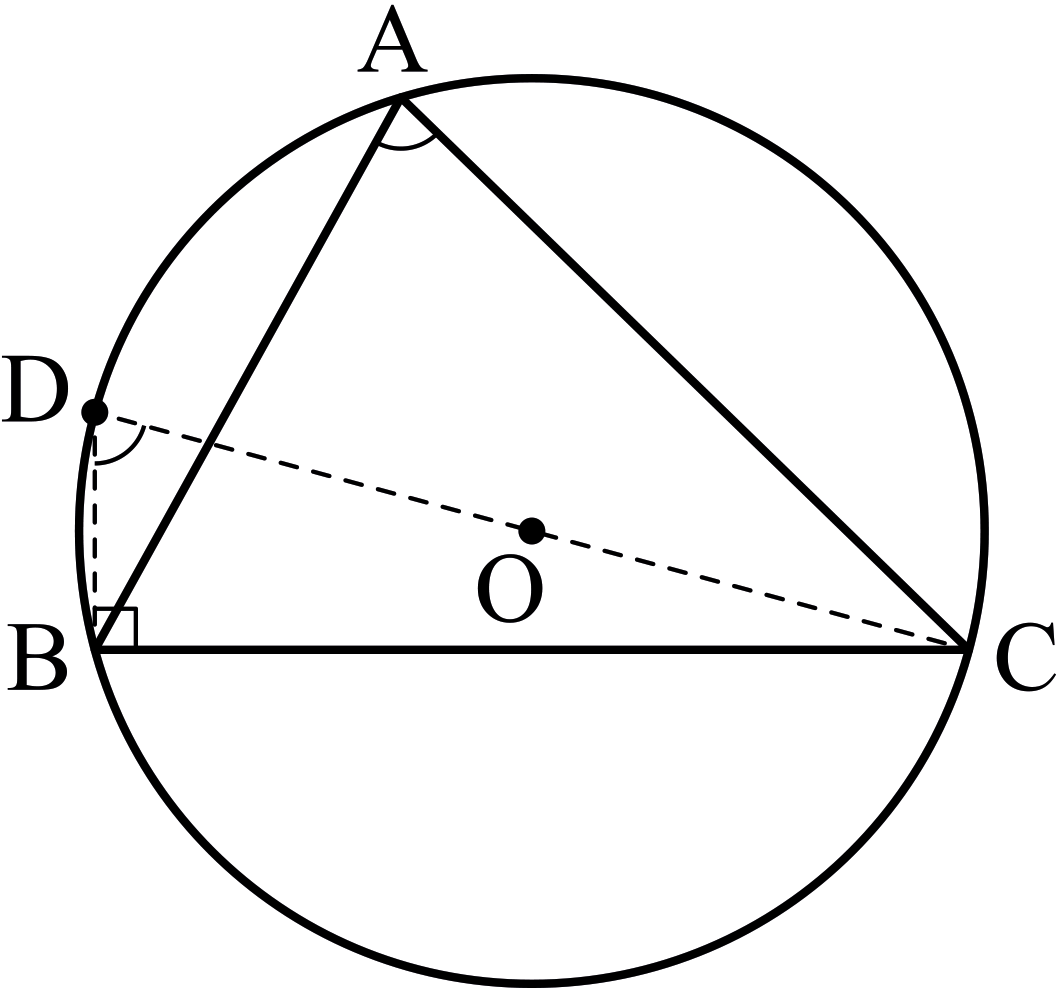
점 \(\mathrm{B}\)와 \(\mathrm{C}\)를 고정하고, 선분 \(\mathrm{DC}\)가 원의 지름이 되도록 점 \(\mathrm{D}\)를 잡는다. 그러면 선분 \(\mathrm{DC}\)의 길이가 \(2R\)이고 \(\angle \mathrm{A} = \angle \mathrm{D}\)이므로 \[2R \sin A = 2R \sin D = a\] 이다. 그러므로 \[\frac{a}{\sin A} = 2R\] 를 얻는다. 같은 방법으로 다른 두 분수식의 값이 \(2R\)라는 사실을 유도할 수 있다.

정리 0.6.3. (삼각함수의 덧셈 정리)

\(\alpha\)와 \(\beta\)가 실수일 때 다음이 성립한다.

  1. \( \sin ( \alpha + \beta ) = \sin \alpha \cos \beta + \cos \alpha \sin \beta \)
  2. \( \sin ( \alpha - \beta ) = \sin \alpha \cos \beta - \cos \alpha \sin \beta \)
  3. \( \cos ( \alpha + \beta ) = \cos \alpha \cos \beta - \sin \alpha \sin \beta \)
  4. \( \cos ( \alpha - \beta ) = \cos \alpha \cos \beta + \sin \alpha \sin \beta \)

증명.

다음 그림을 살펴보자.

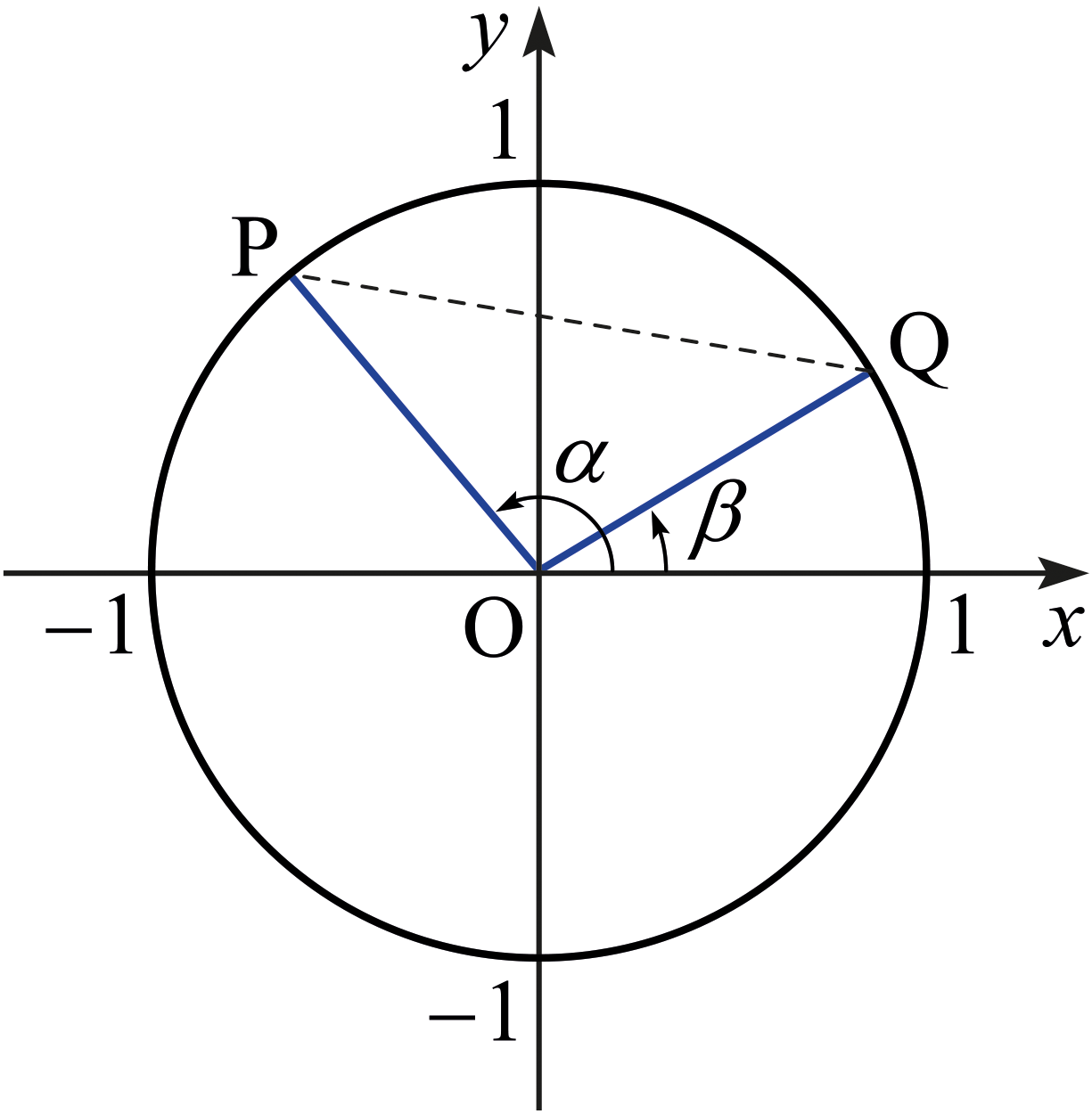
삼각형 \(\mathrm{POQ}\)에 코사인 법칙을 적용하면 다음 등식을 얻는다. \[\overline{\mathrm{PQ}}^2 = \overline{\mathrm{OP}}^2 + \overline{\mathrm{OQ}}^2 - 2 \cdot \overline{\mathrm{OP}} \cdot \overline{\mathrm{OQ}} \cdot \cos ( \alpha - \beta ).\] 그런데 \(\overline{\mathrm{OP}} = \overline{\mathrm{OQ}} = 1\)이므로, 위 식으로부터 다음 등식을 얻는다. \[ ( \cos \alpha - \cos \beta )^2 + ( \sin \alpha - \sin \beta )^2 = 1^2 + 1^2 - 2 \times 1 \times 1 \times \cos ( \alpha - \beta ).\] 이 식과 \[ \sin^2 \alpha + \cos^2 \alpha = 1 , \,\, \sin^2 \beta + \cos^2 \beta = 1 \] 을 결합하면 다음 등식을 얻는다. \[\cos(\alpha - \beta ) = \cos \alpha \cos \beta + \sin \alpha \sin \beta .\] 이 식에서 \(\beta\)를 \(-\beta\)로 바꾸면 다음 등식을 얻는다. \[\cos ( \alpha + \beta ) = \cos \alpha \cos \beta - \sin \alpha \sin \beta .\] 이 식에서 \(\alpha\)를 \(\frac{\pi}{2} - \alpha\)로 바꾸면 \[\cos\left\{ \left( \frac{\pi}{2} - \alpha \right) + \beta \right\} = \cos \left( \frac{\pi}{2} - \alpha \right) \cos\beta - \sin\left(\frac{\pi}{2} - \alpha\right) \sin\beta\] 이므로 다음을 얻는다. \[\sin ( \alpha - \beta ) = \sin \alpha \cos \beta - \cos \alpha \sin \beta .\] 이 식에서 \(\beta\)를 \(-\beta\)로 바꾸면 다음 등식을 얻는다. \[ \sin ( \alpha + \beta ) = \sin \alpha \cos \beta + \cos \alpha \sin \beta . \] 이로써 정리의 등식 [4], [3], [2], [1]을 얻었다.

사실 정리 0.6.3의 증명은 \(\alpha\)와 \(\beta\)가 \(2\pi\) 미만 양수이고, 두 각의 차이가 \(\pi\) 미만인 경우만 증명한 것이다. 하지만 사인과 코사인의 주기성과 앞에서 살펴본 삼각함수의 등식을 이용하면 임의의 각 \(\alpha\)와 \(\beta\)에 대하여 네 개의 등식이 성립함을 확인할 수 있다.