함수의 극한의 성질

by I Seul Bee

이 글은 『미적분학 첫걸음』 3장 2절의 내용입니다.  (미적분학 첫걸음 차례 보기)

이 절에서는 함수의 극한의 성질을 살펴봅니다.

수열의 극한과 함수의 극한의 관계

3.1절에서 함수의 극한을 정의하기 위하여 집적점의 개념을 도입하였다. 그런데 집적점은 수열의 극한을 사용하여 정의된다. 그러므로 함수의 극한과 수열의 극한은 밀접한 연관을 가진다.

정리 3.2.1. (수열 판정법, Sequential Test)

\(f:D \rightarrow \mathbb{R}\)가 함수이고 \(c\)가 \(D\)의 집적점이며, \(L\)이 실수라고 하자. \(x \rightarrow c\)일 때 \(f(x)\)가 \(L\)에 수렴하기 위한 필요충분조건은 세 조건

  • \(n\rightarrow\infty\)일 때 \(x_n \rightarrow c,\)
  • 임의의 \(n\)에 대하여 \(x_n \in D ,\)
  • 임의의 \(n\)에 대하여 \(x_n \ne c\)
를 모두 만족시키는 모든 수열 \(\left\{x_n \right\}\)에 대하여 수열 \(\left\{ f(x_n ) \right\}\)이 \(L\)에 수렴하는 것이다.

보기 3.2.1. \(\chi_\mathbb{Q} : \mathbb{R} \rightarrow \mathbb{R}\)가 특성함수(characteristic function)라고 하자. 즉 \[\chi_\mathbb{Q} (x) = \begin{cases} 1 \quad & \text{if} \,\, x\in\mathbb{Q} ,\\ 0 \quad & \text{if} \,\, x\notin\mathbb{Q} \end{cases}\] 라고 하자. 그리고 \(c\in \mathbb{R}\)가 임의로 주어졌다고 하자. 그러면 \(c\)에 수렴하고 어느 항도 \(c\)와 일치하지 않는 유리수열 \(\left\{ q_n \right\}\)과 무리수열 \(\left\{ r_n \right\}\)이 존재한다.

이제 \(x\rightarrow c\)일 때 \(f(x)\)가 \(L\)에 수렴한다고 가정하자. 그러면 수열 판정법에 의하여 다음 두 등식이 성립한다. \[\begin{gather} \lim_{x\rightarrow c}\chi_\mathbb{Q} (x) = \lim_{n\rightarrow \infty} \chi_\mathbb{Q} (q_n ) = \lim_{n\rightarrow \infty} 1 = 1 , \\[6pt] \lim_{x\rightarrow c}\chi_\mathbb{Q} (x) = \lim_{n\rightarrow \infty} \chi_\mathbb{Q} (r_n ) = \lim_{n\rightarrow \infty} 0 = 0. \end{gather}\] 두 등식으로부터 \(1 = L = 0\)을 얻는데, 이것은 모순이다. 그러므로 \(x\rightarrow c\)일 때 \(f(x)\)는 어떠한 값에도 수렴하지 않는다.

참고. 점에서 발산하는 함수의 극한도 수열 판정법을 사용할 수 있다. \(f:D \rightarrow \mathbb{R}\)가 함수이고 \(c\)가 \(D\)의 집적점이라고 하자. 이때 다음 각각이 성립한다.

  • \(x\rightarrow c\)일 때 \(f(x) \rightarrow \infty\)이기 위한 필요충분조건은 \(c\)에 수렴하고 임의의 \(n\)에 대하여 \(x_n \in D,\) \(x_n \ne c\)인 임의의 수열 \(\left\{ x_n \right\}\)에 대하여 수열 \(\left\{ f(x_n ) \right\}\)이 양의 무한대에 발산하는 것이다.
  • \(x\rightarrow c\)일 때 \(f(x) \rightarrow -\infty\)이기 위한 필요충분조건은 \(c\)에 수렴하고 임의의 \(n\)에 대하여 \(x_n \in D,\) \(x_n \ne c\)인 임의의 수열 \(\left\{ x_n \right\}\)에 대하여 수열 \(\left\{ f(x_n ) \right\}\)이 음의 무한대에 발산하는 것이다.

사칙계산과 관련된 함수의 극한의 성질

수열의 극한과 마찬가지로 함수의 극한도 사칙계산과 관련된 성질을 가지고 있다.

정리 3.2.2. (함수의 극한의 대수적 성질)

\(f\)와 \(g\)가 정의역 \(D\)를 공통으로 갖는 함수이고 \(c\)가 \(D\)의 집적점이라고 하자. 그리고 \(L,\) \(M\)이 실수이며 \[\lim_{x\rightarrow c} f(x) = L \quad\text{and}\quad \lim_{x\rightarrow c}g(x)=M\] 이라고 하자. 그러면 다음이 성립한다.

  1. \(\displaystyle \lim_{x\rightarrow c} (k f(x)) = kL.\)  (\(k\)는 실수인 상수.)
  2. \(\displaystyle \lim_{x\rightarrow c}(f(x)+g(x)) = L+M.\)
  3. \(\displaystyle \lim_{x\rightarrow c}(f(x)-g(x)) = L-M.\)
  4. \(\displaystyle \lim_{x\rightarrow c}(f(x)g(x)) = LM.\)
  5. \(\displaystyle \lim_{x\rightarrow c}\frac{f(x)}{g(x)} = \frac{L}{M}.\)  (단, \(M\ne 0.\))
  6. \(\displaystyle \lim_{x\rightarrow c}\sqrt[m]{f(x)} = \sqrt[m]{L}.\)  (단, \(L\ge 0\)이고, 임의의 \(x\)에 대하여 \(f(x) \ge 0.\))

수열의 극한의 대수적 성질(정리 1.3.1)과 수열 판정법(정리 3.2.1)을 결합하면 정리 3.2.2를 증명할 수 있다. 수열 \(\left\{ x_n \right\}\)이 세 조건

  • \(n \rightarrow \infty\)일 때 \(x_n \rightarrow c,\)
  • 임의의 \(n\)에 대하여 \(x_n \in D,\)
  • 임의의 \(n\)에 대하여 \(x_n \ne c\)
를 만족시킨다고 하자. 그러면 수열 판정법에 의하여 \[\lim _ {n\rightarrow\infty} f(x_n ) = L \quad\text{and}\quad \lim_{n\rightarrow\infty} g(x_n ) = M\] 이 성립한다. 수열의 극한의 대수적 성질에 의하여 \[\lim_{n\rightarrow\infty}(f(x_n) + g(x_n)) = \lim_{n\rightarrow\infty}f(x_n) + \lim_{n\rightarrow\infty}g(x_n) = L+M\] 이다. 앞의 세 조건을 만족시키는 임의의 수열 \(\left\{x_n\right\}\)에 대하여 이 등식이 성립하므로 수열 판정법에 의하여 \[\lim_{x\rightarrow c}(f(x)+g(x)) = L+M\] 이 성립한다. 즉 [2]를 증명하였다. 다른 등식의 증명도 이와 같다.

보기 3.2.2.

  1. \[\begin{align} \lim_{x\rightarrow 2} (x^2 -2x +3 ) &= \lim_{x\rightarrow 2} x^2 - \lim_{x\rightarrow 2} 2x + \lim_{x\rightarrow 2} 3 \\[5pt] &= \left( \lim_{x\rightarrow 2} x \right) \left( \lim_{x\rightarrow 2} x \right) - 2 \times \left( \lim_{x\rightarrow 2} x \right) + \lim_{x\rightarrow 2} 3 \\[5pt] &= 2 \times 2 - 2 \times 2 + 3 = 3. \end{align}\]
  2. \[\begin{align} \lim_{x\rightarrow -3} \frac{x^2 -x+1}{x+1} &= \frac{\displaystyle \lim_{x\rightarrow -3} (x^2 -x+1)}{\displaystyle \lim_{x\rightarrow -3} (x+1)} \\[5pt] &= \frac{(-3)^2 -(-3) +1}{(-3)+1} = - \frac{13}{2}. \end{align}\]

보기 3.2.3.

  1. \[\begin{align} \lim_{x\rightarrow 1} \frac{\sqrt{x} -1}{x-1} &= \lim_{x\rightarrow 1} \frac{(\sqrt{x} -1)(\sqrt{x}+1)}{(x-1)(\sqrt{x}+1)} \\[5pt] &= \lim_{x\rightarrow 1} \frac{x-1}{(x-1)(\sqrt{x}+1)} \\[5pt] &= \lim_{x\rightarrow 1} \frac{1}{\sqrt{x}+1} = \frac{1}{2}. \end{align}\]
  2. \[\begin{align} \lim_{h\rightarrow 0} \frac{\sqrt{2+h} - \sqrt{2}}{h} &= \lim_{h\rightarrow 0} \frac{(\sqrt{2+h} - \sqrt{2})(\sqrt{2+h} + \sqrt{2})}{h(\sqrt{2+h} + \sqrt{2})} \\[5pt] &= \lim_{h\rightarrow 0} \frac{2+h-2}{h(\sqrt{2+h} + \sqrt{2})} \\[5pt] &= \lim_{h\rightarrow 0} \frac{1}{\sqrt{2+h} + \sqrt{2}} \\[5pt] &= \lim_{h\rightarrow 0} \frac{1}{\sqrt{2} + \sqrt{2}} = \frac{1}{2\sqrt{2}}. \end{align}\]

과제.

  1. \(p\)가 다항함수이고 \(c\)가 실수라고 하자. 이때 \[\lim_{x\rightarrow c}p(x) = p(c)\] 임을 보이시오.
  2. \(p\)와 \(q\)가 다항함수이고 \(c\)가 실수이며 \(q(c) \ne 0\)이라고 하자. 이때 \[\lim_{x\rightarrow c} \frac{p(x)}{q(x)} = \frac{p(c)}{q(c)}\] 임을 보이시오.

예제 3.2.4. 다음 등식이 성립하도록 하는 실수 \(a,\) \(b\)의 값을 구하시오. \[\lim_{x\rightarrow 2} \frac{2x^2 +ax+b}{x-2} = 3.\]

풀이. \(x\rightarrow 2\)일 때 분모가 \(0\)에 수렴하는데 분수식이 발산하지 않으므로 분자 또한 \(0\)에 수렴해야 한다. 즉 \[\lim_{x\rightarrow 2} (2x^2 +ax+b)=0\] 이다. 이 식으로부터 \(8+2a+b=0\) 즉 \(b = -2a-8\)을 얻는다. 원래의 극한에서 \(b\)를 \(-2a-8\)로 바꾸면 다음 식을 얻는다. \[\lim_{x\rightarrow 2}\frac{2x^2 +ax-2a-8}{x-2} = 3.\] 이 등식에서 좌변을 계산하면 다음과 같다. \[\lim_{x\rightarrow 2}\frac{(2x+a+4)(x-2)}{x-2} = \lim_{x\rightarrow 2}(2x+a+4) = a+8.\] 그러므로 \(a=-5,\) \(b=2\)를 얻는다.

순서관계와 관련된 함수의 극한의 성질

수열의 극한과 마찬가지로 함수의 극한도 순서관계와 관련된 성질을 가진다.

정리 3.2.3. (순서보존 성질)

\(f\)와 \(g\)가 공통정의역 \(D\)에서 정의된 함수이고 \(c\)가 \(D\)의 집적점이라고 하자. 또한 \(c\)를 원소로 갖는 열린 구간 \(I\)가 존재하여 임의의 \(x\in (I\cap D)\setminus\left\{ c \right\}\)에 대하여 \(f(x) \le g(x)\)를 만족시킨다고 하자. 이때 다음이 성립한다.

  1. 만약 \(x\rightarrow c\)일 때 \(f(x)\)와 \(g(x)\)가 각각 \(L,\) \(M\)에 수렴하면 \(L\le M\)이다.
  2. 만약 \(x\rightarrow c\)일 때 \(f(x)\)가 양의 무한대에 발산하면 \(g(x)\)도 양의 무한대에 발산한다.
  3. 만약 \(x\rightarrow c\)일 때 \(g(x)\)가 음의 무한대에 발산하면 \(f(x)\)도 음의 무한대에 발산한다.

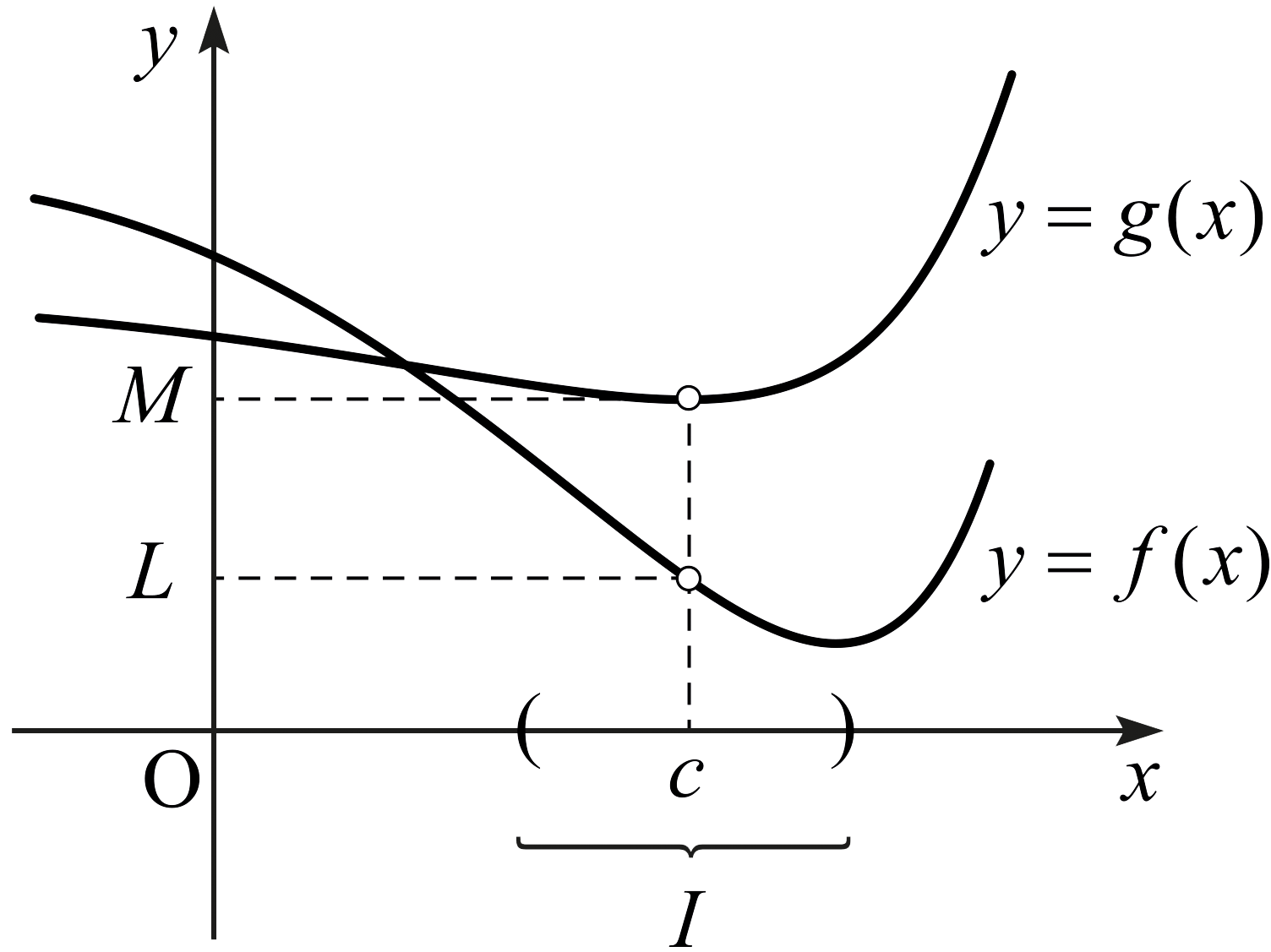
세 개의 함수를 비교하면 다음과 같다.

정리 3.2.4. (조임 정리)

\(f,\) \(g,\) \(h\)가 공통정의역 \(D\)에서 정의된 함수이고 \(c\)가 \(D\)의 집적점이라고 하자. 또한 \(c\)를 원소로 갖는 열린 구간 \(I\)가 존재하여 임의의 \(x\in (I\cap D)\setminus\left\{ c \right\}\)에 대하여 \(f(x) \le g(x) \le h(x)\)를 만족시킨다고 하자. 만약 \(x\rightarrow c\)일 때 \(f(x)\)와 \(h(x)\)가 같은 값 \(L\)에 수렴하면, \(x\rightarrow c\)일 때 \(g(x)\)도 \(L\)에 수렴한다.

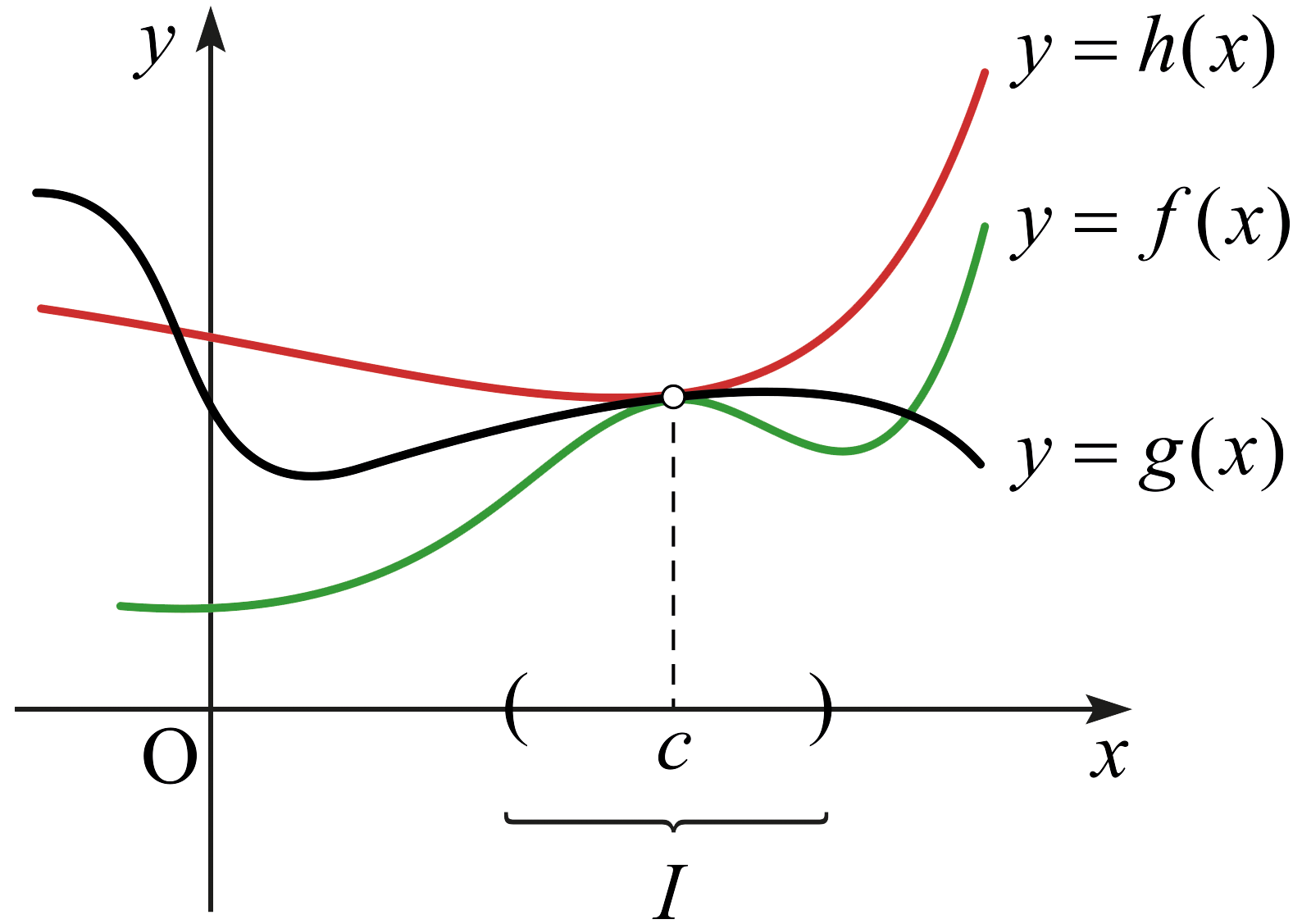
보기 3.2.5. 함수 \(f:\mathbb{R}^{\times} \rightarrow \mathbb{R}\)가 다음과 같이 주어졌다고 하자. \[f(x) = x\sin \frac{1}{x}.\] (여기서 \(\mathbb{R}^\times = \mathbb{R} \setminus\left\{ 0 \right\}\)이다.) \[g(x) = \lvert x \rvert\] 라고 하자. 그러면 임의의 \(x\in\mathbb{R}^\times\)에 대하여 \[-g(x) \le f(x) \le g(x)\] 이다. 그런데 \[\lim_{x\rightarrow 0} (-g(x)) = \lim_{x\rightarrow 0} g(x) =0\] 이므로, 조임 정리에 의하여 \[\lim_{x\rightarrow 0} g(x)=0\] 이다.

예제 3.2.6. 다음 극한을 조사하시오. \[\lim_{x\rightarrow 0}\frac{\sin x}{x}.\] (여기서 ‘극한을 조사한다’라는 말은 극한이 수렴하는지 판별하고, 수렴한다면 극한값을 구하라는 뜻이다.)

풀이. \(x\)가 \(0\)에 가까울 때만 생각해도 충분하다. 먼저 \(0 < x < \pi /2\)인 경우를 살펴보자.

아래 그림을 보자.

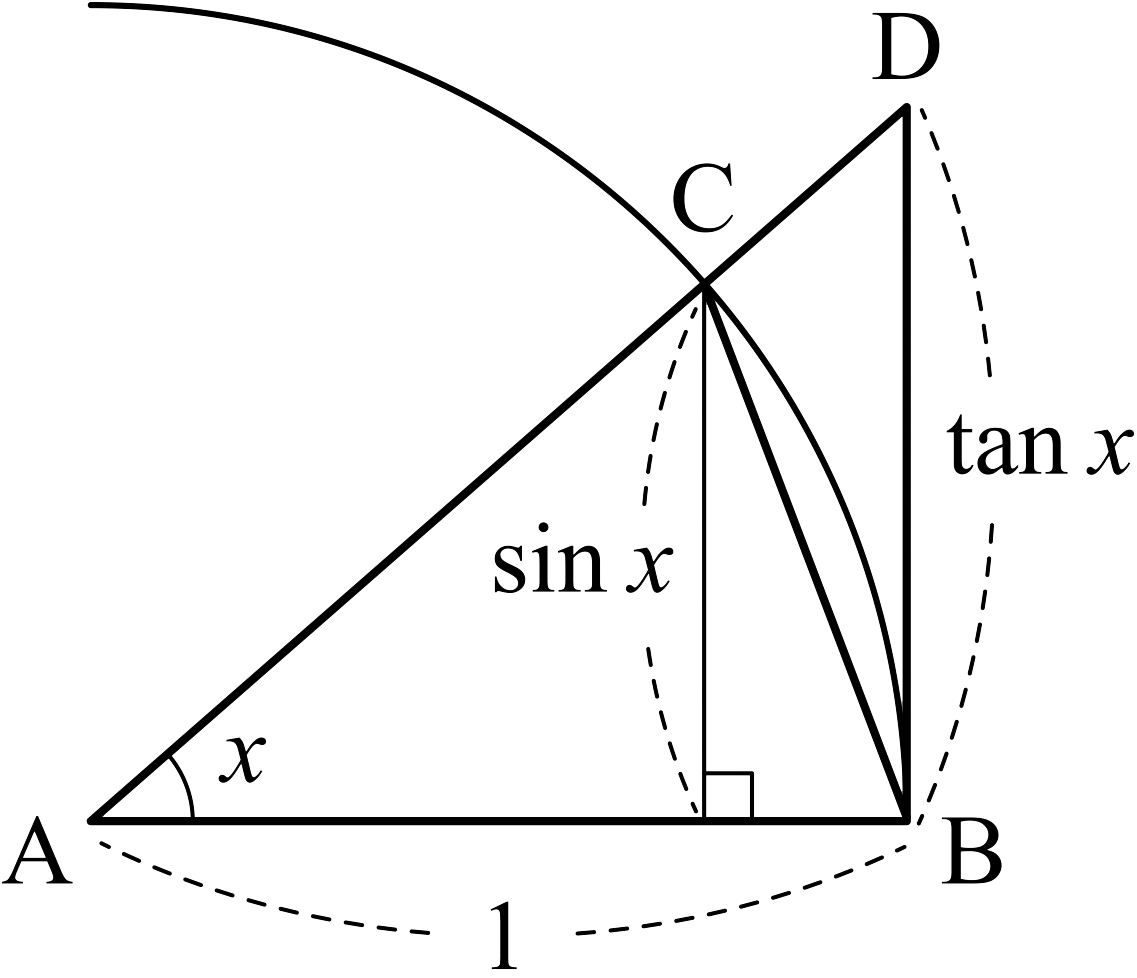
  • 삼각형 \(\mathrm{ABC}\)의 넓이는 \(\frac{1}{2}\sin x\)이다.
  • 부채꼴 \(\mathrm{ABC}\)의 넓이는 \(\frac{1}{2} x\)이다.
  • 삼각형 \(\mathrm{ABD}\)의 넓이는 \(\frac{1}{2}\tan x\)이다.

그림에서 넓이를 비교하면 다음 부등식을 얻는다. \[\frac{1}{2} \tan x \ge \frac{1}{2} x \ge \frac{1}{2} \sin x .\] 각 식을 \(\frac{1}{2} \sin x\)로 나누고 역수를 취하면 다음을 얻는다. \[\cos x \le \frac{\sin x}{x} \le 1.\] 여기서 \(\cos x\)와 \(\frac{\sin x}{x}\)가 모두 우함수이므로, 위 부등식은 \( - \frac{\pi}{2} < x < 0\)일 때도 성립한다. 더욱이 \[\lim_{x\rightarrow 0}\cos x = 1 \quad\text{and}\quad \lim_{x\rightarrow 0} 1 = 1\] 이다. 그러므로 조임 정리에 의하여 \[\lim_{x\rightarrow 0} \frac{\sin x}{x} = 1\] 이 성립한다.

예제 3.2.7. 다음 극한을 구하시오. \[\lim_{x\rightarrow 0} \frac{1-\cos x}{x} .\]

풀이. 극한을 구할 분수식을 변형하면 다음과 같다. \[\begin{align} \frac{1-\cos x}{x} &= \frac{(1-\cos x)(1+ \cos x)}{x(1+\cos x)} \\[5pt] &= \frac{1-\cos ^2 x}{x(1+\cos x)} \\[5pt] &= \frac{\sin^2 x}{x(1+ \cos x )}. \end{align}\] 이 결과를 이용하여 문제의 극한을 계산하면 다음과 같다. \[\begin{align} \lim_{x\rightarrow 0}\frac{1-\cos x }{x} &= \lim_{x\rightarrow 0} \frac{\sin^2 x}{x(1+\cos x)} \\[5pt] &= \lim_{x\rightarrow 0} \left\{ \frac{\sin x}{x} \times \frac{\sin x}{1+\cos x} \right\} \\[5pt] &= 1\times \frac{0}{2} = 0. \end{align}\]