이 글은 『미적분학 첫걸음』 3장 1절의 내용입니다. (미적분학 첫걸음 차례 보기)
함수 \(f:D \rightarrow \mathbb{R}\)가 주어졌다고 하자. 점 \(c\)에서 \(f\)의 극한을 정의하려면 변수 \(x\)가 \(c\)에 한없이 가까이 다가갈 수 있어야 한다. 따라서 함수의 극한을 정의하기 전에 집적점의 개념을 도입하자.
\(D\)가 공집합이 아닌 집합이고 \(c\)가 수라고 하자. 여기서 \(c\)가 \(D\)의 원소일 필요는 없다. 만약 세 조건
- \(n\rightarrow\infty\)일 때 \(c_n \rightarrow c,\)
- 임의의 \(n\)에 대하여 \(c_n \ne c,\)
- 임의의 \(n\)에 대하여 \(c_n \in D\)
를 모두 만족시키는 수열 \(\left\{ c_n \right\}\)이 존재하면, \(c\)를 \(D\)의 집적점(cluster point)이라고 부른다.
보기 3.1.1.
- \(I\)가 길이가 양수인 구간이면 \(I\)의 모든 점은 \(I\)의 집적점이다.
- \(D = \left\{ \frac{1}{n} \,\vert\, n\in\mathbb{N}\right\}\)이면 \(0\)은 \(D\)의 집적점이다. \(D\)는 \(0\) 이외의 집적점을 갖지 않는다. 여기서 \(0\)이 \(D\)에 속하지 않는다는 사실에 유의하자.
- 유리수 전체 집합을 \(\mathbb{Q}\)라고 하자. 모든 실수는 \(\mathbb{Q}\)의 집적점이다.
- \(E\)가 \(\mathbb{R}\)의 유한부분집합이면 \(E\)는 집적점을 갖지 않는다.
- \(\left\{ a_n \right\}\)이 모든 항이 서로 다른 수열이라고 하자. 그러면 집합 \(\left\{ a_n \,\vert\, n\in\mathbb{N}\right\}\)의 집적점과 수열 \(\left\{a_n\right\}\)의 집적점이 일치한다.
- \(\left\{ b_n \right\}\)이 상수 수열이면 집합 \(\left\{ b_n \,\vert\, n\in\mathbb{N}\right\}\)은 집적점을 갖지 않는다.
이제 함수의 극한을 정의하자. 함수 \(f:D \rightarrow \mathbb{R}\)가 주어졌다고 하자. 그리고 \(c\)가 \(D\)의 집적점이라고 하자.
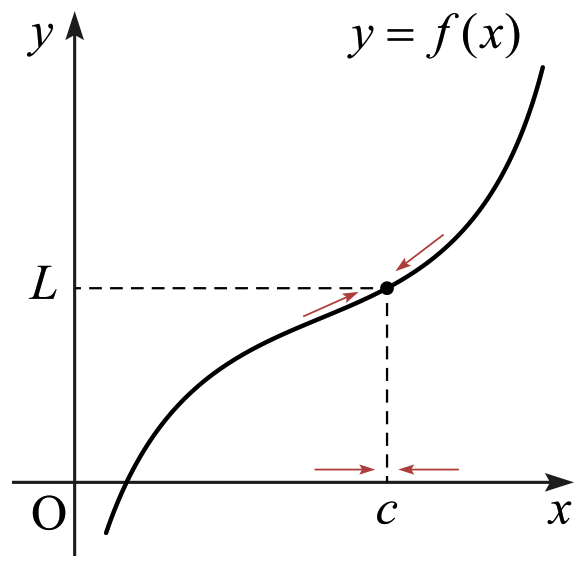
만약 \(x\)가 \(x\ne c\)를 유지한 채로 \(c\)에 한없이 가까이 다가갈 때 \(f(x)\)의 값이 하나의 값 \(L\)에 한없이 가까이 다가가면
“\(c\)에서 \(f(x)\)가 \(L\)에 수렴한다.”
또는
“\(x\)가 \(c\)에 다가갈 때 \(f(x)\)가 \(L\)에 수렴한다.”
또는
“\(x\)가 \(c\)에 다가갈 때 \(f(x)\)가 \(L\)에 다가간다.”
라고 말한다. 이때 \(L\)을 \(c\)에서 \(f\)의 극한(limit)이라고 부른다. 이 사실을 기호로 \[\lim_{x\rightarrow c}f(x) = L\] 또는 \[f(x) \rightarrow L \quad \text{as} \quad x\rightarrow c\] 와 같이 나타낸다.
보기 3.1.2. 함수 \(f:\mathbb{R}\rightarrow\mathbb{R}\)가 \(f(x) = 2x-1\)로 주어졌다고 하자. \(3\)은 \(f\)의 정의역의 집적점이다. \(x\)가 \(x\ne 3\)이면서 \(3\)에 가까이 다가간다고 하자. 더 명확하게 말하자면, \(x\)와 \(3\) 사이의 거리 \(\lvert x-3 \rvert\)이 \(d\)를 넘지 않는다고 하자. 그러면 \(f(x)\)와 \(5\) 사이의 거리는 \[\lvert f(x) - 5 \rvert = \lvert (2x-1)-5 \rvert = 2 \lvert x-3 \rvert\] 이며, 이 값은 \(2d\)를 넘지 않는다. 그러므로 \(x\)가 \(3\)에 다가가면 \(f(x)\)의 값은 \(5\)에 다가간다. 즉 \[\lim_{x\rightarrow 3} f(x)=5\] 이다.
보기 3.1.3. 함수 \(f:\mathbb{R}\rightarrow\mathbb{R}\)가 \(f(x) = x^2 -3\)으로 주어졌다고 하자. \(1\)은 \(f\)의 정의역이 집적점이다. \(x\)가 \(1\)에 다가갈 때 \(x^2 - 3\)이 \(-2\)에 다가간다. 즉 \[\lim_{x\rightarrow 1}\left( x^2 -3 \right) =-2\] 이다.
보기 3.1.4. 함수 \(f\)가 \(D = (-\infty ,\,3) \cup (3,\,\infty )\)에서 다음과 같이 정의되었다고 하자. \[f(x) = \frac{x^2 -x-6}{x-3}.\] \(3\)이 \(D\)이 집적점이므로 \(3\)에서 \(f\)의 극한을 생각할 수 있다. [‘극한을 생각할 수 있다’는 말이 ‘극한이 존재한다’는 뜻이 아니다.] 만약 \(x\ne 3\)이면 \[f(x) = \frac{x^2 -x-6}{x-3} = \frac{(x-3)(x+2)}{x-3} = x+2\] 이다.
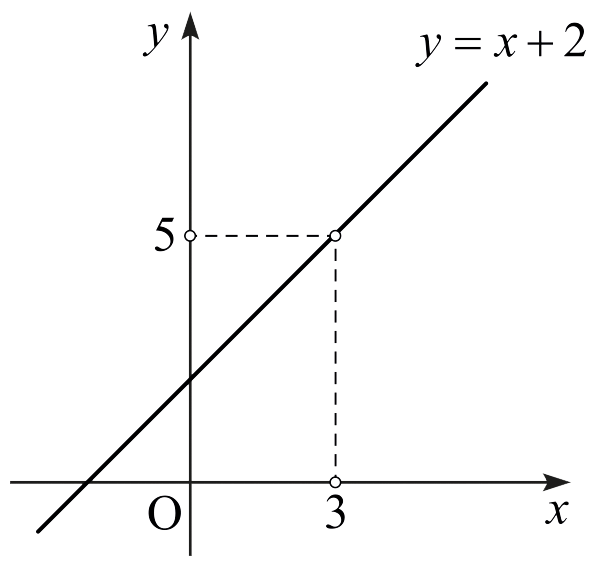
그러므로 \(x\)가 \(3\)에 다가가면 \(f(x)\)의 값은 \(5\)에 다가간다. 즉 \[\lim_{x\rightarrow 3}\frac{x^2 -x-6}{x-3} = 5\] 이다.
만약 \(f(x)\)가 \(c\)에서 수렴하지 않는다면, 즉 만약 \(x\)가 \(x\ne c\)를 유지한 채로 \(c\)에 다가가지만 \(f(x)\)의 값은 하나의 값에 다가가지 않는다면,
“\(x\)가 \(c\)에 다가갈 때 \(f(x)\)가 발산(diverge)한다.”
또는
“\(c\)에서 \(f(x)\)가 발산한다.”
라고 말한다.
보기 3.1.5. 함수 \(f:\mathbb{R} \rightarrow \mathbb{R}\)가 \(f(x) = \lfloor x \rfloor\)로 주어졌다고 하자. 여기서 \(\lfloor x \rfloor\)는 최대정수함수이다. \(x\)가 \(2\)에 다가간다고 하자.
만약 \(x < 2\)이면서 \(x\)가 \(2\)에 다가간다면 \(f(x)\)는 \(1\)에 다가간다. 만약 \(x > 2\)이면서 \(x\)가 \(2\)에 다가간다면 \(f(x)\)는 \(2\)에 다가간다. 즉 \(2\)에서 \(f\)는 하나의 값에 수렴하지 않는다. 따라서 \(f\)는 \(2\)에서 발산한다.
만약 \(x\)가 \(x\ne c\)를 유지한 채 \(c\)에 다가갈 때 \(f(x)\)의 값이 한없이 커지면 “\(x\rightarrow c\)일 때 \(f(x)\)가 양의 무한대에 발산한다.”라고 말한다. 이것을 기호로 \[\lim_{x\rightarrow c}f(x)=\infty\] 와 같이 나타낸다.
만약 \(x\)가 \(x\ne c\)를 유지한 채 \(c\)에 다가갈 때 \(f(x)\)의 값이 한없이 작아지면 “\(x\rightarrow c\)일 때 \(f(x)\)가 음의 무한대에 발산한다.”라고 말한다. 이것을 기호로 \[\lim_{x\rightarrow c}f(x)=-\infty\] 와 같이 나타낸다.
만약 \(x\rightarrow c\)일 때 \(f(x)\)가 발산하지만 양의 무한대나 음의 무한대에 발산하지 않는다면 “\(x\rightarrow c\)일 때 \(f(x)\)가 진동한다(oscillate)”라고 말한다.
보기 3.1.6.
- 만약 \(f(x) = \frac{1}{x^2}\)이면 \[\lim_{x\rightarrow 0}f(x) = \infty\]이다.
- 만약 \(f(x) = \ln \lvert x \rvert\)이면 \[\lim_{x\rightarrow 0} f(x) = -\infty\]이다.
- 만약 \(f(x) = \frac{1}{x}\)이면 \(x\rightarrow 0\)일 때 \(f(x)\)는 진동한다.
- 만약 \(f(x) = \lfloor x \rfloor\)이고 \(n\)이 정수이면, \(x\rightarrow n\)일 때 \(f(x)\)는 진동한다.
- 만약 \(f(x) = \sin \frac{1}{x}\)이면 \(x \rightarrow 0\)일 때 \(f(x)\)는 진동한다.
- 만약 \(f(x) = \lvert \tan x \rvert\)이면 \[\lim_{x\rightarrow\frac{\pi}{2}} f(x) =\infty\] 이다.
- 앞의 글 : 교대급수
- 다음 글 : 함수의 극한의 성질
