이 글은 『미적분학 첫걸음』 6장 2절의 내용입니다. (미적분학 첫걸음 차례 보기)
6장 1절에서 정적분을 정의하고 어떠한 함수가 적분 가능한지 살펴보았다. 이 절에서는 정적분을 계산하는 방법을 살펴보자.
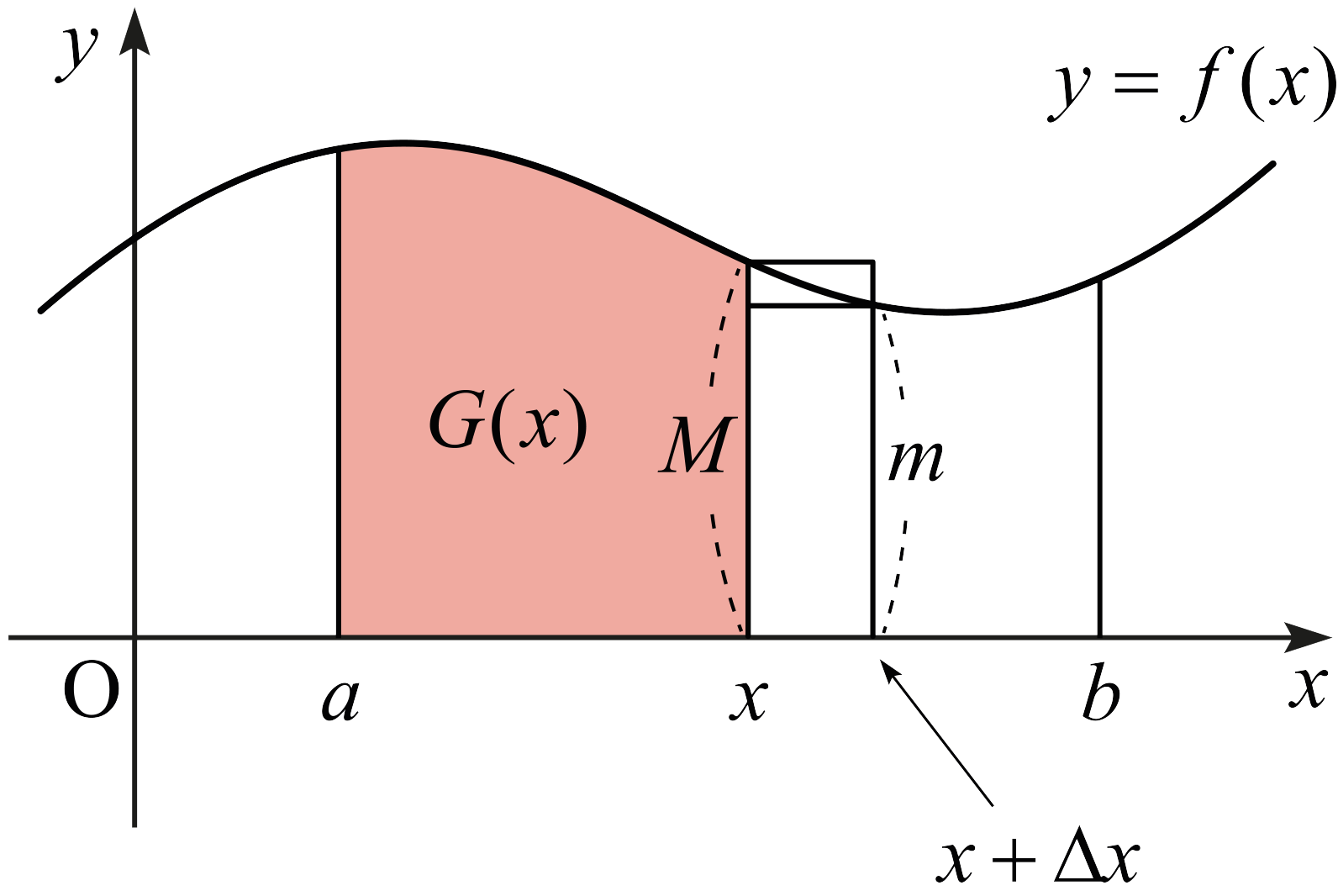
\(a < b\)이고 \(f\)가 \(I=[a,\,b]\)에서 정의된 연속인 실숫값 함수라고 하자. \(x\in I\)에 대하여 \[ G(x) = \int_a^x f(t) dt \] 라고 하자. 이제 \(a\le x < b\)라고 하고 \(\Delta x\)가 \(a < x + \Delta x \le b\)를 만족시키는 작은 양수라고 하자. 닫힌구간 \(\left[ x ,\, x+\Delta x \right]\)에서 \(f\)의 최솟값과 최댓값을 각각 \(m,\) \(M\)이라고 하자. (여기서 \(m\)과 \(M\)은 \(\Delta x\)에 따라 변하는 값임을 생각하자.) 다음 그림을 보자.
소구간 \(\left[x,\,x+\Delta x\right]\)에서 \[ m\le f(t)\le M \] 이므로 정적분의 성질에 의하여 \[ m\Delta x \le G(x+\Delta x) - G(x) \le M\Delta x \] 를 얻는다. 각 식을 \(\Delta x\)로 나누면 다음을 얻는다. \[ m \le \frac{G(x+\Delta x) - G(x)}{\Delta x} \le M. \] 함수 \(f\)가 \(\left[ x,\, x+\Delta x\right]\)에서 연속이므로 \[ f( \xi_1 ) = m ,\quad f(\xi _2 ) = M \] 인 \(\xi_1 \)과 \(\xi _2\)가 \(\left[ x,\, x+\Delta x \right]\)에 존재한다. 즉 \[ f(\xi_1 ) \le \frac{G(x+\Delta x) - G(x)}{\Delta x} \le f(\xi_2 ) \] 이다. \(\Delta x \rightarrow 0^+\)일 때 \(\xi_1 \rightarrow x\)이고 \(\xi_2 \rightarrow x\)이며, \(f\)가 \(x\)에서 연속이므로 \[ f(\xi_1 ) \rightarrow f(x) ,\quad f(\xi_2 ) \rightarrow f(x) \] 이다. 그러므로 \(x\)에서 \(G\)의 우미분계수는 \[ G_r ' (x) = f(x) \] 이다. \(a < x\le b\)이고 \(\Delta x\)가 작은 음수인 경우에도 같은 방법으로 \(x\)에서 \(G\)의 좌미분계수가 \[ G_l ' (x) = f(x) \] 가 됨을 보일 수 있다.
지금까지 다음 정리를 증명하였다.
정리 6.2.1. (적분으로 정의된 함수)
함수 \(f\)가 구간 \(I = [a,\,b]\)에서 정의된 연속인 실숫값 함수이고 \[ G(x) = \int_a^x f(t) dt \] 라고 하자. 그러면 \(x\in I\)에 대하여 \(G ' (x) = f(x)\)이다.
앞의 가정을 그대로 둔 상태에서, \(F\)가 \(I\)에서 \(f\)의 한 역도함수라고 하자. 그러면 \(x\in I\)에 대하여 \[ F ' (x) = f(x) = G ' (x) \] 이므로 상수 \(C\)가 존재하여 임의의 \(x\in I\)에 대하여 \[ G(x) = F(x) +C \] 를 만족시킨다. 이 등식에서 \(x\)에 \(a\)를 대입하면 \[ F(a) +C = G(a)=0 \] 이므로 \(C = -F(a)\)를 얻는다. 즉 \[ G(x) = F(x) - F(a) \] 이다. 이 등식에서 \(x\)에 \(b\)를 대입하면 \[ G(b) = F(b) - F(a) \] 를 얻는다. \(G(b)\)를 적분 기호로 바꾸어 나타내면 \[ \int_a^b f(x)dx = F(b) -F(a) \] 를 얻는다.
지금까지 다음 정리를 증명하였다.
정리 6.2.2. (미적분의 기본정리)
함수 \(f\)가 구간 \(I=[a,\,b]\)에서 정의된 연속인 실숫값 함수이고, \(F\)가 \(I\)에서 \(f\)의 역도함수라고 하자. 그러면 \[ \int_a^b f(x) dx = F(b) -F(a) \] 이다.
미적분의 기본정리에서 등식의 우변을 다음과 같이 나타내기도 한다. \[ \int_a^b f(x) dx = F(x) \bigg\vert_a^b \] 또는 \[ \int_a^b f(x) dx = \bigg[ F(x) \bigg]_a^b . \] \(F(x)\)가 하나의 항으로 이루어져 있다면 두 표현 중 어느 것을 사용해도 무방하다. \(F(x)\)가 둘 이상의 항으로 이루어져 있다면 혼동을 피하기 위하여 두 번째 표현을 사용하거나, 첫 번째 표현에서 \(F(x)\)의 항 전체를 괄호로 묶어 나타낼 수 있다.
예제 6.2.1. 다음 적분을 구하시오. \[ \int_0^1 x \,dx . \]
풀이. \(f(x) =x ,\) \(F(x) = \frac{1}{2} x^2\)이라고 하면 \(F ' = f\)이다. 그러므로 미적분의 기본정리에 의하여 \[ \int_0^1 x\,dx = \int_0^1 f(x) dx = F(1) - F(0) = \frac{1}{2} -0 = \frac{1}{2} \] 이다.
예제 6.2.2. 다음 적분을 구하시오. \[ \int_0^1 x^2 \,dx . \]
풀이. \(g(x) =x^2 ,\) \(G(x) = \frac{1}{3} x^3\)이라고 하면 \(G ' = g\)이다. 그러므로 미적분의 기본정리에 의하여 \[ \int_0^1 x^2 \,dx = \int_0^1 g(x) dx = G(1) - G(0) = \frac{1}{3} -0 = \frac{1}{3} \] 이다.
참고. 미적분의 기본정리(정리 6.2.2)에서 \(f\)의 역도함수 \(F\)는 어느 것을 택하든 상관없다. 예컨대 \(F_1\)이 \(f\)의 또 다른 역도함수라면 상수 \(C_1\)이 존재하여 임의의 \(x\in [a,\,b]\)에 대하여 \(F(x) = F_1 (x) + C_1\)을 만족시킨다. 그러므로 \[ \begin{align} \int_a^b f(x) dx &= F(b) - F(a) \\[5pt] &= (F_1 (b) + C_1 ) - ( F_1 (a) + C_1 ) \\[5pt] &= F_1 (b) - F_1 (a) \end{align} \] 가 성립한다.
함수 \(f\)가 \([a,\,b]\)에서 미분 가능하고 \(f ' \)이 \([a,\,b]\)에서 적분 가능하다고 하자. 그리고 \(x_i\)가 \[ a = x_0 < x_1 < x_2 < \cdots < x_{i-1} < x_i < \cdots < x_{n-1} < x_n = b \] 를 만족시키는 \((n+1)\)개의 점이라고 하자. 이 점들의 모임을 \(P\)라고 하자. 그러면 평균값 정리에 의하여, \(i=1,\,2,\,\cdots,\,n\)일 때 \(x_{i-1}\)과 \(x_i\) 사이에 점 \(c_i\)가 존재하여 다음을 만족시킨다. \[ f ' (c_i ) = \frac{f(x_i ) - f(x_{i-1})}{x_i - x_{i-1}} . \] 이 식을 변형하면 \[ f(x_i ) - f(x_{i-1}) = f ' (c_i ) \Delta x_i \] 이다. \(i=1\)일 때부터 \(i=n\)일 때까지 위 식을 변마다 더하면 \[ f(b) - f(a) = \sum_{i=1}^n f ' (c_i ) \Delta x_i \] 를 얻는다. 한편 \[ L(f ',\,P) \le \sum_{i=1}^n f ' (c_i ) \Delta x_i \le U(f ',\,P) \] 이고 \(f ' \)이 \([a,\,b]\)에서 적분 가능하므로, \(\lVert P \rVert \rightarrow 0\)일 때 위 등식의 우변은 \([a,\,b]\)에서 \(f ' \)의 적분값에 수렴한다.
지금까지 다음 정리를 증명하였다.
정리 6.2.3. (도함수의 정적분)
함수 \(f\)가 구간 \([a,\,b]\)에서 미분 가능하고 \(f ' \)이 \([a,\,b]\)에서 적분 가능하면 \[ \int_a^b f ' (x) dx = f(b)-f(a) \] 이다.
참고. 함수 \(f\)가 \([a,\,b]\)에서 미분 가능할지라도 \(f ' \)은 \([a,\,b]\)에서 적분 가능하지 않을 수 있다. 예컨대 함수 \(f\)가 \([-1,\,1]\)에서 다음과 같이 주어졌다고 하자. \[ f(x) = \begin{cases} x^2 \sin\frac{1}{x^3} \quad &\text{if} \,\, x\ne 0 , \\[5pt] 0 \quad &\text{if} \,\, x =0. \end{cases} \] 그러면 \[ f ' (x) = \begin{cases} 2x\sin\frac{1}{x^3} - \frac{3}{x^2} \cos\frac{1}{x^3} \quad &\text{if} \,\, x\ne 0 , \\[5pt] 0 \quad &\text{if} \,\, x=0 \end{cases} \] 이다. 따라서 \(f ' \)은 \(0\)을 원소로 갖는 구간에서 유계가 아니다.
그러므로 \(f ' \)은 \([-1,\,1]\)에서 적분 불가능하다.