연속의 정의

by I Seul Bee

이 글은 『미적분학 첫걸음』 4장 1절의 내용입니다.  (미적분학 첫걸음 차례 보기)

함수 \(f:D \rightarrow \mathbb{R}\)가 주어져 있고, \(c\)가 \(D\)의 점이라고 하자. 만약 다음 두 가지 중 하나가 성립하면 “\(f\)가 \(c\)에서 연속이다(continuous)”라고 말한다.

  • \(c\)가 \(D\)의 집적점이고 \(\displaystyle\lim_{x\rightarrow c} f(x)=f(c)\)이다.
  • \(c\)가 \(D\)의 집적점이 아니다.

\(c\)가 \(f\)의 정의역의 점이고 \(f\)가 \(c\)에서 연속이 아니면 “\(f\)가 \(c\)에서 불연속이다(discontinuous)”라고 말한다.

함수 \(f\)가 \(c\)에서 불연속이지만 \(c\)에서 \(f\)의 좌극한과 우극한이 모두 존재하면, “\(f\)가 \(c\)에서 단순불연속이다”라고 말한다(simple discontinuity). 함수 \(f\)가 \(c\)에서 불연속이고 \(c\)가 \(f\)의 단순불연속점이 아니면, \(c\)를 \(f\)의 제 2 종 불연속점이라고 부른다(second kind discontinuity).

함수 \(f\)가 정의역의 모든 점에서 연속이면 \(f\)를 연속함수(continuous function)라고 부른다.

점 \(c\)가 함수 \(f\)의 정의역의 집적점이라고 하자. 그러면 \(f\)가 \(c\)에서 연속인지 판별하기 위해서는 다음 세 조건이 모두 만족되는지를 살피면 된다.

  • \(f(c)\)가 정의된다.  (\(c\)에서 \(f\)의 함숫값이 존재한다.)
  • \(\displaystyle\lim_{x\rightarrow c}f(x)\)가 존재한다.  (\(c\)에서 \(f\)의 극한이 수렴한다.)
  • \(\displaystyle\lim_{x\rightarrow c}f(x) = f(c).\)  (\(c\)에서 \(f\)의 극한값과 함숫값이 일치한다.

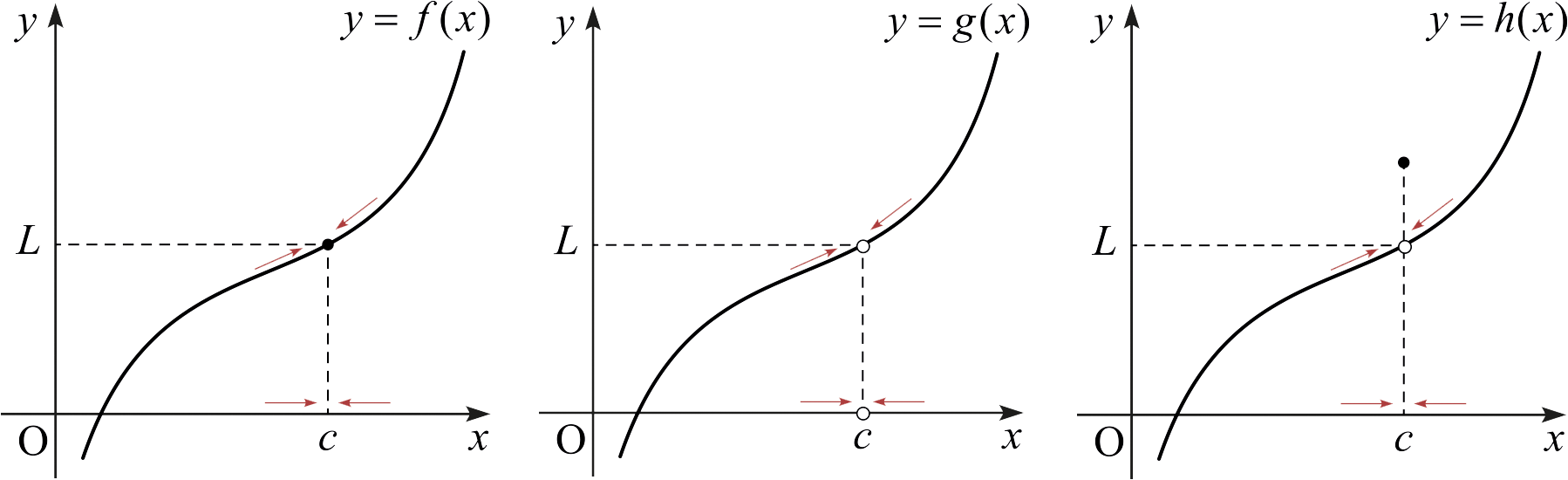
함수 \(f,\) \(g,\) \(h\)의 그래프가 아래 그림과 같을 때, 함수 \(f\)는 점 \(c\)에서 연속이고 함수 \(g\)와 \(h\)는 점 \(c\)에서 연속이 아니다.

보기 4.1.1.

  1. 함수 \(f\)가 \(f(x)=x^2\)으로 주어졌다고 하자. 그러면 \(f\)는 \(\mathbb{R}\)에서 연속인 함수이다 왜냐하면 \(\mathbb{R}\)의 모든 점에서 \(f\)의 극한값과 함숫값이 일치하기 때문이다.
  2. 함수 \(g\)가\[g(x)=\frac{x^2 -x-6}{x-3}\]으로 주어졌다고 하자. 그러면 \(g\)는 \(3\)에서 연속이 아니다. 왜냐하면 \(3\)은 \(g\)의 정의역의 원소가 아니기 때문이다. \(g\)는 \(3\)을 제외한 모든 점에서 연속이다.
  3. 함수 \(h\)가 \[h(x) = \lfloor x \rfloor\]로 주어졌다고 하자. 즉 \(h\)가 최대정수함수라고 하자. 만약 \(n\)이 정수이면 \(h\)는 \(n\)에서 연속이 아니다. 왜냐하면 \(n\)에서 \(h\)의 극한이 수렴하지 않기 때문이다. 하지만 \(n\)에서 \(h\)의 좌극한과 우극한이 모두 존재하므로 \(h\)는 \(n\)에서 단순불연속이다. 만약 \(c\)가 정수가 아닌 실수라면 \(h\)는 \(c\)에서 연속이다.
  4. 함수 \(f\)가 \(\mathbb{Z}\)에서 정의되었다면 \(f\)는 \(\mathbb{Z}\)의 모든 점에서 연속이다. 왜냐하면 \(\mathbb{Z}\)의 임의의 점은 \(\mathbb{Z}\)의 집적점이 아니기 때문이다.
  5. 함수 \(g\)가 \(g(x)=\chi_\mathbb{Q} (x)\)로 정의되었다면 \(g\)는 어느 점에서도 연속이 아니다. \(g\)는 임의의 점에서 제 2 종 불연속이다.

함수의 극한의 성질로부터 다음 정리를 얻는다.

정리 4.1.1.

두 함수 \(f\)와 \(g\)가 같은 정의역을 갖는 함수라고 하자. 만약 \(f\)와 \(g\)가 모두 \(c\)에서 연속이면 다음이 성립한다.

  1. \(f+g\)가 \(c\)에서 연속이다.
  2. \(f-g\)가 \(c\)에서 연속이다.
  3. \(k\)가 상수이면 \(kf\)가 \(c\)에서 연속이다.
  4. \(g(c) \ne 0\)이면 \(f/g\)가 \(c\)에서 연속이다.
  5. \(m\)이 양의 정수이고 \(f\ge 0\)이면 \(\sqrt[m]{f}\)가 \(c\)에서 연속이다.

보기 4.1.2.

  1. 모든 다항함수는 \(\mathbb{R}\)에서 연속이다.
  2. \(p(x)\)와 \(q(x)\)가 다항식이면 \[f(x) = \frac{p(x)}{q(x)}\] 로 정의된 유리함수 \(f\)는 \(q(x)=0\)의 근을 제외한 점에서 연속이다.

예제 4.1.3. \(a\)와 \(b\)가 상수이고 함수 \(f:\mathbb{R} \rightarrow \mathbb{R}\)가 다음과 같이 주어졌다. \[f(x) = \begin{cases} \displaystyle \frac{x^2 -2x +a}{x-1} & \quad \text{if}\,\, x\ne 1 \\ b+1 & \quad \text{if}\,\, x=1 \end{cases}\] 이때 \(f\)가 \(\mathbb{R}\)에서 연속이 되도록 하는 \(a\)와 \(b\)의 값을 각각 구하시오.

풀이. \(f\)가 \(1\)에서 연속이므로 \[\lim_{x\rightarrow 1}f(x) = f(1)\] 즉 \[\lim_{x\rightarrow 1} \frac{x^2 -2x+a}{x-1} =b+1\tag{a}\] 이다. \(x\rightarrow 1\)일 때 위 등식의 좌변의 분모가 \(0\)에 수렴하므로 분자도 \(0\)에 수렴해야 한다. 그러므로 \[\lim_{x\rightarrow 1} \left(x^2 -2x+a \right) = a-1 =0\] 즉 \(a=1\)이다. 이 값을 (a)에 대입하면 \[\lim_{x\rightarrow 1} \frac{x^2 -2x+1}{x-1} = b+1\] 이다. 이 식을 풀면 \[0 = b+1\] 이므로 \(b=-1\)이다.

\(I = [a,\,b]\)가 길이가 양수인 닫히 구간이고 \(f\)가 \(I\)에서 정의된 함수라고 하자. 만약 \(f\)가 다음 세 조건을 모두 만족시키면 “\(f\)가 구간 \(\boldsymbol{I}\)에서 연속이다”라고 말한다.

  1. \(a < c < b\)인 모든 점 \(c\)에서 \(f\)가 연속이다.
  2. \(\displaystyle \lim_{x\rightarrow a^+} f(x) = f(a)\)이다. 즉 \(f\)가 \(a\)에서 우연속이다. (continuous on the right at \(a.\))
  3. \(\displaystyle \lim_{x\rightarrow b^-} f(x) = f(b)\)이다. 즉 \(f\)가 \(b\)에서 좌연속이다. (continuous on the left at \(b.\))

위 정의에서 함수 \(f\)의 정의역 전체를 고려하면 \(f\)가 \(a\)나 \(b\)에서 연속이 아닐 수 있다.

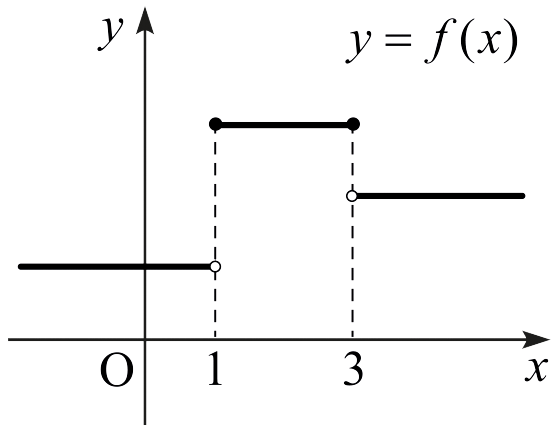
보기 4.1.4. 함수 \(f\)가 \(\mathbb{R}\)에서 다음과 같이 정의되었다고 하자. \[f(x) = \begin{cases} 1 & \quad \text{if} \,\, x < 1 \\[4pt] 3 & \quad \text{if} \,\, 1 \le x \le 3 \\[4pt] 2 & \quad \text{if} \,\, x > 3 \end{cases}\] 이 함수의 그래프는 아래 그림과 같다.

함수 \(f\)는 \(1\)과 \(3\)에서 불연속이다. 그럼에도 불구하고 \(f\)는 닫힌구간 \([1,\,3]\)에서 연속이다.