이 글은 『미적분학 첫걸음』 3장 5절의 내용입니다. (미적분학 첫걸음 차례 보기)
직관적으로, 그래프 위의 점이 원점으로부터 한 없이 멀어질 때 그 점이 하나의 직선에 한 없이 가까워지면, 가까워지는 그 직선을 함수의 그래프의 점근선이라고 부른다. 이 절에서는 세 가지 종류의 점근선, 즉 수평점근선, 사선점근선, 수직점근선을 살펴보자.
수평점근선
직선 \(y=b\)가 함수 \(y=f(x)\)의 그래프의 수평점근선(horizontal asymptote)이라 함은 다음을 만족시키는 것을 의미한다. \[\lim_{x\rightarrow\infty} f(x) = b \quad\text{or}\quad \lim_{x\rightarrow -\infty} f(x)=b .\]
보기 3.5.1.
- 만약 \(f(x)=\frac{1}{x}\)이면 \[\lim_{x\rightarrow\infty} \frac{1}{x} =0 \quad\text{and}\quad \lim_{x\rightarrow -\infty} \frac{1}{x}=0\] 이다. 그러므로 \(y=f(x)\)의 그래프는 하나의 수평점근선 \(y=0\)을 가진다.
- 만약 \(f(x)=e^x\)이면 \[\lim_{x\rightarrow\infty} e^x = \infty \quad\text{and}\quad \lim_{x\rightarrow -\infty} e^x = 0\] 이다. 그러므로 \(y=f(x)\)의 그래프는 하나의 수평점근선 \(y=0\)을 가진다.
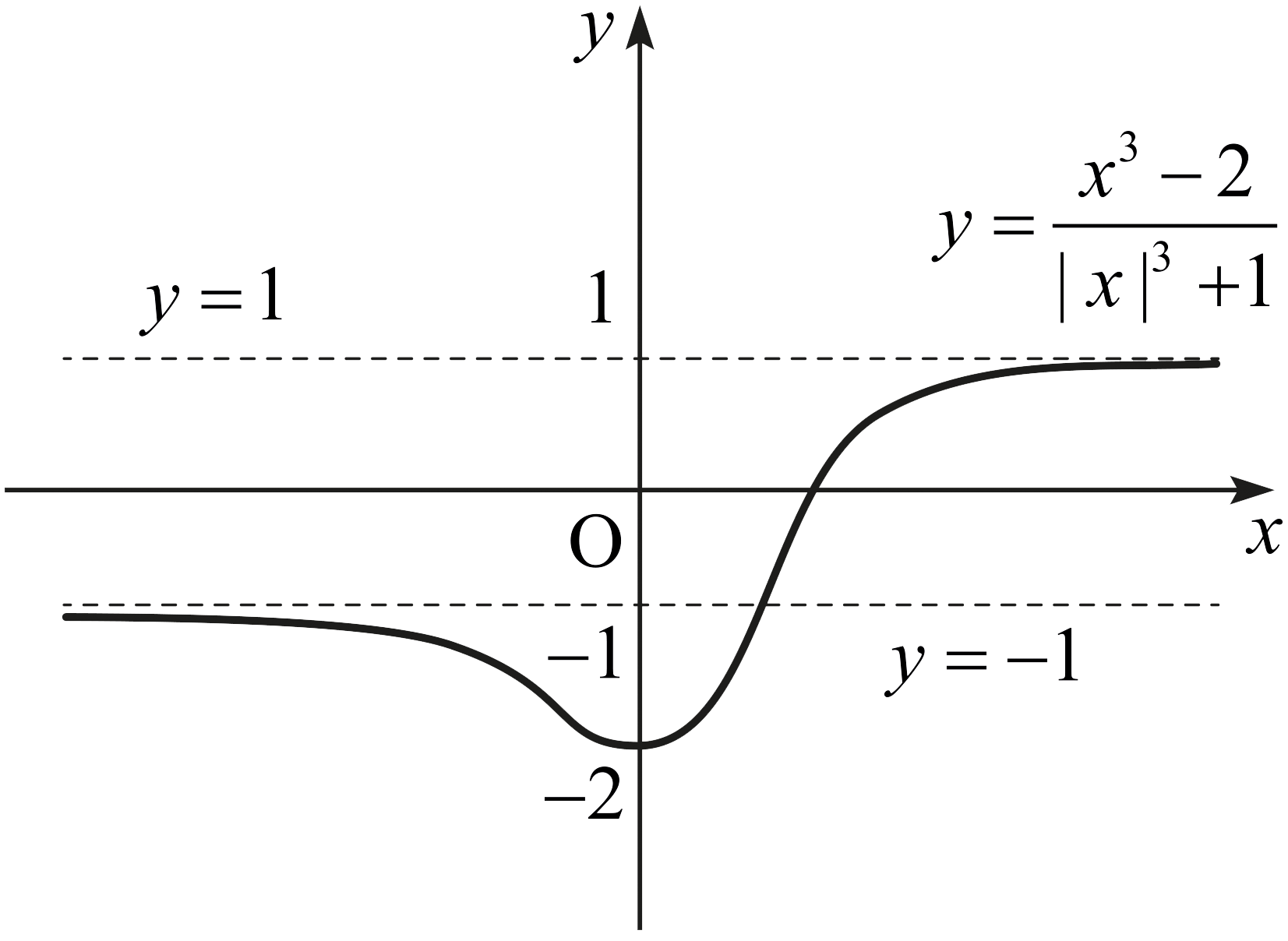
- 함수 \(f\)가 다음과 같이 주어졌다고 하자. \[f(x) = \frac{x^3 -2}{\lvert x \rvert ^3 +1}.\] 그러면 \[\lim_{x\rightarrow\infty} \frac{x^3 -2}{\lvert x \rvert ^3 +1} =1 \quad\text{and}\quad \lim_{x\rightarrow -\infty} \frac{x^3 -2}{\lvert x \rvert ^3 +1} =-1\] 이다. 그러므로 \(y=f(x)\)의 그래프는 서로 다른 두 개의 직선 \(y=1\)과 \(y=-1\)을 수평점근선으로 가진다.
- \(f(x) = \sin x\)라고 하자. 그러면 \(x\rightarrow \infty\)일 때와 \(x\rightarrow -\infty\)일 때 모두 \(\sin x\)가 진동한다. 그러므로 \(y=f(x)\)의 그래프는 수평점근선을 갖지 않는다.
- \(f(x) = \frac{\sin x}{x}\)라고 하자. 그러면 \[\lim_{x\rightarrow\infty} \frac{\sin x}{x} = 0 \quad\text{and}\quad \lim_{x\rightarrow -\infty} \frac{\sin x}{x} = 0\] 이므로, \(y=f(x)\)의 그래프는 하나의 수평점근선 \(y=0\)을 가진다. 이 경우 \(y=f(x)\)의 그래프와 점근선 \(y=0\)이 무수히 많은 점에서 교차한다는 점이 흥미로운 특징이다.
사선점근선
직선 \(y=ax+b\)가 함수 \(y=f(x)\)의 그래프의 사선점근선(oblique asymptote)이라 함은 \(a \ne 0\)이면서 직선 \(y=0\)이 \(y=f(x)-ax-b\)의 수평점근선인 것을 의미한다. ‘oblique asymptote’을 ‘slant line asymptote’라고 부르기도 한다.
보기 3.5.2.
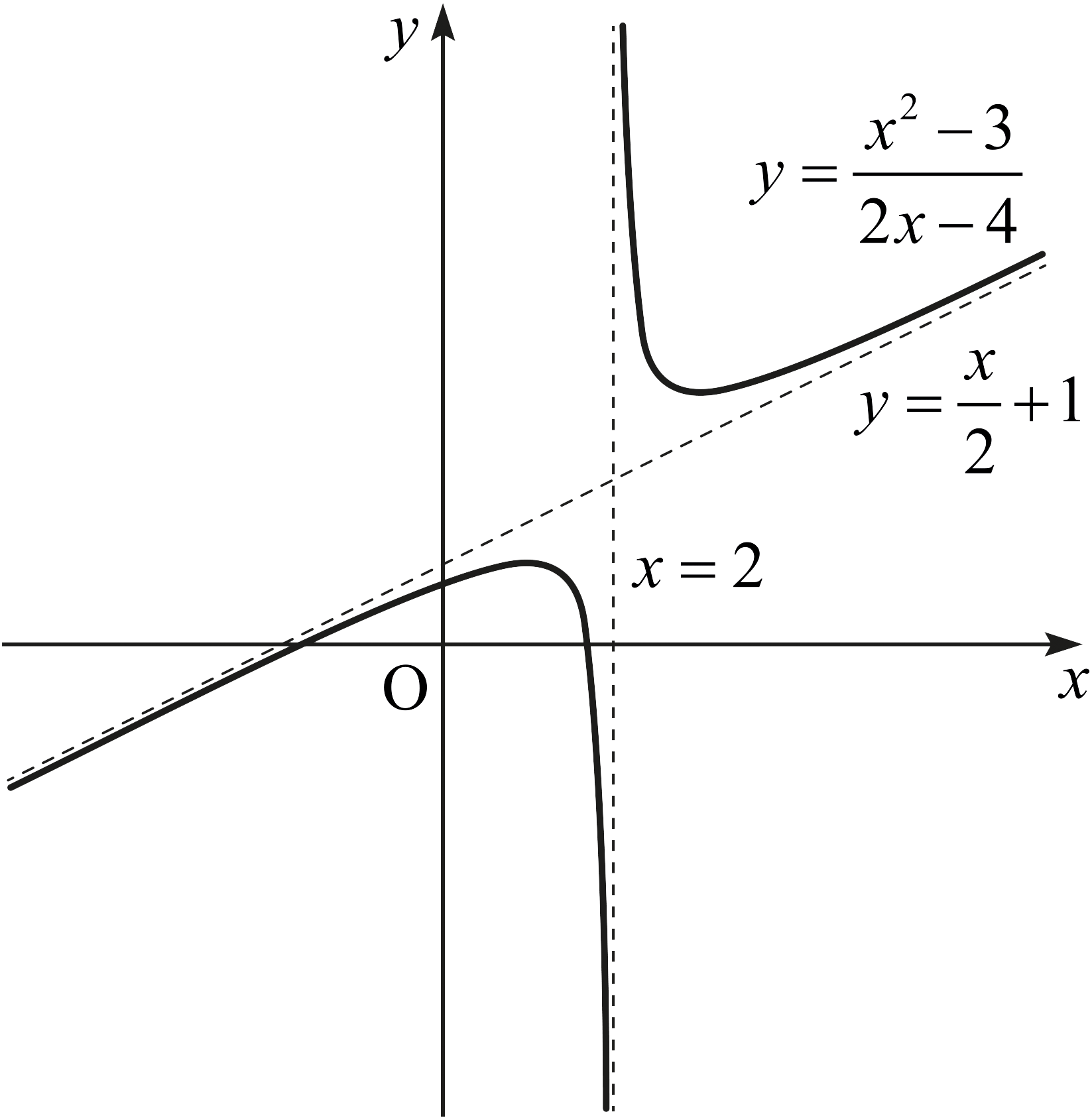
- 함수 \(f\)가 다음과 같이 주어졌다고 하자. \[f(x) = \frac{x^2 -3}{2x-4}.\] \(g(x) = \frac{x}{2} +1\)이라고 하면 \[\lim_{x\rightarrow\infty} (f(x)-g(x)) = \lim_{x\rightarrow\infty} \frac{1}{4-2x} = 0\] 그리고 \[\lim_{x\rightarrow -\infty} (f(x)-g(x)) = \lim_{x\rightarrow -\infty} \frac{1}{4-2x} = 0\] 이다. 즉 \(y=f(x)\)는 하나의 사선점근선 \(y=\frac{x}{2} +1\)을 가진다.
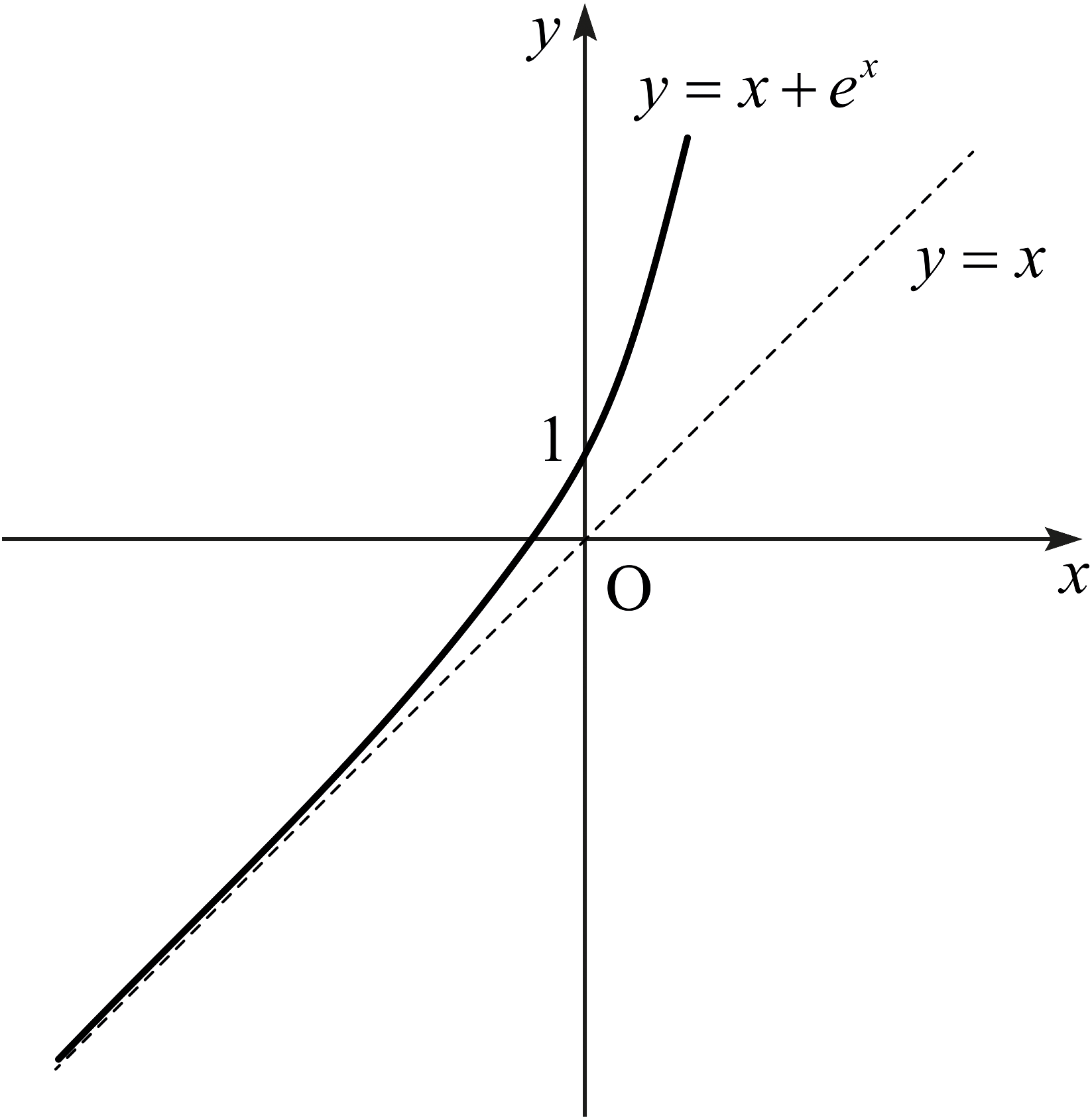
- \(f(x) = x+e^x\)이라고 하자. 그러면 임의의 \(a,\) \(b\)에 대하여 \[\lim_{x\rightarrow\infty} \left\{ x+e^x - (ax+b)\right\} = \infty\] 이고 \[\lim_{x\rightarrow -\infty} \left\{ x + e^x - x\right\} = 0\] 이다. 그러므로 \(y=f(x)\)의 그래프는 하나의 사선점근선 \(y=x\)를 가진다.
- 만약 \(f(x)=\cos x\)이면, \(y=f(x)\)의 그래프는 사선점근선을 갖지 않는다.
수직점근선
직선 \(x=c\)가 함수 \(y=f(x)\)의 그래프의 수직점근선(vertical asymptote)이라 함은 다음을 만족시키는 것을 의미한다. \[\lim_{x\rightarrow c^+} f(x) = \pm \infty \quad\text{or}\quad \lim_{x\rightarrow c^-} f(x) =\pm\infty .\]
보기 3.5.3.
- 만약 \(f(x) = \frac{1}{x}\)이면 \(f\)는 \(0\)을 제외한 모든 점에서 연속이다. 그리고 \[\lim_{x\rightarrow 0^+} \frac{1}{x} = \infty \quad\text{and}\quad \lim_{x\rightarrow 0^-} \frac{1}{x} = -\infty\] 이므로 \(y=f(x)\)의 그래프는 하나의 수직점근선 \(x=0\)을 가진다.
- 만약 \(f(x) = \tan x\)이면 \[x = n \pi + \frac{\pi}{2} ,\,\, n\in\mathbb{Z}\] 꼴의 임의의 직선은 \(y=f(x)\)의 그래프의 수직점근선이다. 이 외의 다른 수직점근선은 존재하지 않는다. 수직직점근선의 수가 무한히 많을 수 있다는 사실이 흥미로운 점이다.
- \(f(x)=\ln x\)라고 하자. 그러면 \(f\)의 정의역은 \((0,\, \infty )\)이며, \(f\)는 \((0,\, \infty )\)에서 연속이다. 그런데 \[\lim_{x\rightarrow 0^+} f(x) =-\infty\] 이므로 \(y=f(x)\)의 그래프는 하나의 수직점근선 \(x=0\)을 가진다.
- 만약 \(f(x)=e^x\)이면 \(y=f(x)\)의 그래프는 수직점근선을 갖지 않는다. (\(f\)가 임의의 실수에서 연속이기 때문이다.)
- 앞의 글 : 무한대를 포함한 극한
- 다음 글 : 연속의 정의
