This set of exercises is retrieved from the second chapter of Linear Algebra by Robert J. Valenza. Note that these solutions are not fully elaborated; You have to fill the descriptions by yourself.
Problem 2.1
Give an example of a noncommutative group of \(24\) elements.
Solution. \(S_4 .\)
Problem 2.2
Give an example of a group \(G\) and a nonempty subset \(H\) of \(G\) which is closed under the operation defined on \(G,\) but is not a subgroup of \(G.\)
Solution. Let \(G = \mathbb{Z}\) and the operation be the ordinary addition. Take \(H\) be the set of positive integers. Then \(H\) is a subset of \(G\) and is closed under the ordinary addition. But \(H\) is not a group, because any element of \(H\) does not have an inverse element in \(H.\)
Problem 2.3
Show that a group \(G\) is commutative if and only if the following statement holds:
\[(st)^{-1} = s^{-1} t^{-1} \text{ for all } s,\, t \in G .\tag{*}\]
Solution. If \(G\) is commutative, then \[(st)^{-1} =(ts)^{-1} = s^{-1} t^{-1}.\] Now we prove the converse. Suppose (*) holds. Let \(x,\) \(y\) be elements of \(G.\) Since \(G\) is a group, the inverse elements \(x^{-1}\) and \(y^{-1}\) exist in \(G.\) Therefore, taking \(s= x^{-1}\) and \(t = y^{-1} ,\) we have \[xy = (x^{-1})^{-1} (y^{-1})^{-1} = (x^{-1} y^{-1})^{-1} = ((yx)^{-1})^{-1} = yx\] by (*), that is, \(G\) is a commutative group.
Problem 2.4
Show that the following Cayley table can only be completed in one way so that the elements \(s,\) \(t,\) \(u\) and \(v\) constitute a group. Deduce the requisite products, rigorously defending each step.
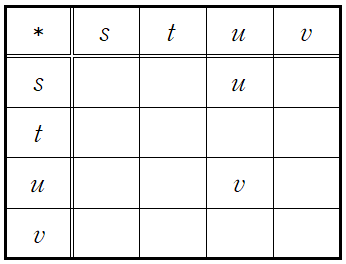
Solution.
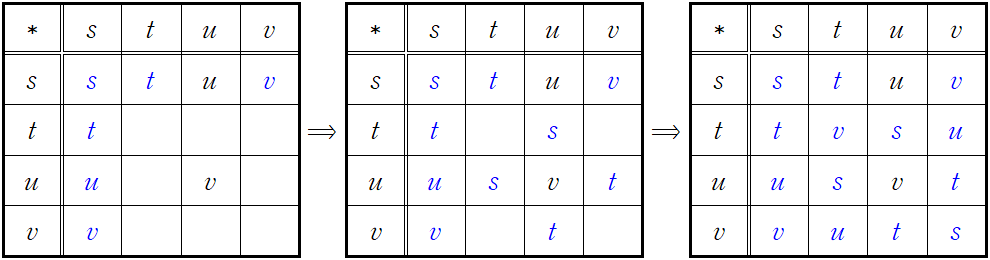
Problem 2.5
Let \(G_0\) and \(G_1\) be groups. Consider the set
\[G_0 \times G_1 = \left\{ ( s_0 ,\, s_1 ) \,\vert\, s_0 \in G_0 ,\, s_1 \in G_1 \right\}.\]
This is just the Cartesian product of the two sets \(G_0\) and \(G_1 .\) Define an operation on \(G_0 \times G_1\) as follows:
\[(s_0 ,\,s_1) (t_0 ,\,t_1 ) = (s_0 t_0 ,\, s_1 t_1 )\]
for all \(s_0 ,\,t_0 \in G_0\) and \(s_1 ,\,t_1 \in G_1 .\) That is, we carry out the product componentwise, making use of the operation defined on the factor groups. Show that \(G_0 \times G_1\) is a group with respect to this operation. Be sure to verify all requisite properties explicitly. This is called the direct product of \(G_0\) and \(G_1 .\)
Solution.
- It is trivial that \(G_0 \times G_1\) is closed under the operation.
- Let \(e_0\) and \(e_1 \) be the identity elements of \(G_0\) and \(G_1\) respectively. Then \((e_0 ,\, e_1 )\) is the identity element of \(G_0 \times G_1 .\)
- Associativity directly comes from that of \(G_0\) and \(G_1 .\)
- Let \((s ,\,t)\) be in \(G_0 \times G_1 ,\) then \((s^{-1} ,\, t^{-1})\) is the inverse element of \((s ,\,t)\), where \(s^{-1} \in G_0\) and \(t^{-1} \in G_1 .\)
Problem 2.6
Show that \(G_0 \times G_1 \cong G_1 \times G_0 .\)
Solution. Take \(\phi (( s,\,t)) = (t,\,s)\) then \(\phi\) is an isomorphism from \(G_0 \times G_1\) to \(G_1 \times G_0 .\)
Problem 2.7
Continuing in the same context, consider the functions
\[\begin{gather}
\rho_0 : G_0 \times G_1 \rightarrow G_0 ,\,\, (s_0 ,\, s_1 ) \mapsto s_0 ,\\[7pt]
\rho_1 : G_0 \times G_1 \rightarrow G_1 ,\,\, (s_0 ,\, s_1 ) \mapsto s_1 .
\end{gather}\]
These are called projection maps. The first, \(\rho_0 ,\) retains the first coordinate and drops the second. The second, \(\rho_1 ,\) retains the second and drops the first. Show that both maps are surjective homomorphisms and compute the kernel of each.
Solution. WLOG, we only have to prove for \(\rho_0 .\)
- Let \(e_1\) be the identity element of \(G_1 .\) For any \(s\in G_0 ,\) \(\rho_0 (s ,\,e_1 ) = s ,\) that is, \(\rho_0\) is surjective.
- Let \((s_0 ,\,s_1 )\) and \((t_0 ,\,t_1 )\) be elements of \(G_0 \times G_1 .\) Then \[\rho_0 ((s_0 ,\,s_1)(t_0 ,\,t_1)) = \rho_0 ((s_0 t_0 ,\, s_1 t_1 )) = s_0 t_0 = \rho_0 ((s_0 ,\, s_1 )) \rho_0 ((t_0 ,\,t_1 )),\] that is, \(\rho_0\) is a homomorphism.
- Let \(e_0\) be the identity element of \(G_0 .\) Then the kernel of \(\rho_0\) is \[\left\{ (e_0 ,\, s_1) \,\vert\, s_1 \in G_1 \right\} .\]
Problem 2.8
Consider the special case of the direct product \(G \times G\) of a group \(G\) with itself. Define a subset \(D\) of \(G\times G\) by
\[D = \left\{ (s,\,s) \,\vert\, s\in G \right\}.\]
That is, \(D\) consists of all elements with both coordinates equal. Show that \(D\) is a subgroup of \(G \times G.\) This is called the diagonal subgroup.
Solution. First, \(D\) is closed under the operation. Besides, for any \((s,\,s)\) and \((t,\,t)\) in \(D,\) we have \[ s \in G ,\,\, t \in G ,\,\, t^{-1} \in G ,\,\, st^{-1} \in G \] and \[ (s,\,s) (t,\,t)^{-1} = (s,\,s)(t^{-1} ,\,t^{-1}) = (st^{-1} ,\, st^{-1}) \in D.\] Therefore, by one-step test, \(D\) is a subgroup of \(G.\)
Problem 2.9
Consider the direct product \(\mathbb{R} \times \mathbb{R}\) of the additive group of real numbers with itself and the function \(f:\mathbb{R} \times \mathbb{R} \rightarrow \mathbb{R}\) defined by \(f(x,\,y) = 2x-y .\) Show that \(f\) is a homomorphism of groups; describe its kernel and image.
Solution. Let \((x_1 ,\,y_1 )\) and \((x_2 ,\,y_2 )\) be elements of \(\mathbb{R}\times\mathbb{R}.\) Then \[\begin{align} f((x_1 ,\, y_1 ) + (x_2 ,\,y_2)) &= f((x_1 + x_2 ,\, y_1 + y_2 )) \\[7pt] &= 2(x_1 + x_2) - (y_1 + y_2) \\[7pt] &= (2x_1 - y_1) + (2x_2 - y_2 ) \\[7pt] &= f((x_1 ,\,y_1)) + f((x_2 ,\,y_2)), \end{align}\] that is, \(f\) is a homomorphism. Its kernel is \[\left\{ (x,\,y) \,\vert\, 2x-y = 0 \right\}\] and its image is \(\mathbb{R}.\)
Problem 2.10
Show that the function \(f: \mathbb{R} \rightarrow \mathbb{R}\) defined by \(f(x) = ax+b\), where \(a,\) \(b\in\mathbb{R}\) and \(b \ne 0,\) is not a homomorphism of additive groups from \(\langle \mathbb{R} ,\, + \rangle\) to itself.
Solution. \(f(0) \ne 0.\)
Problem 2.11
Let \(G\) be a group and consider the additive group of integers \(\mathbb{Z}.\) For any fixed \(s\in G,\) show that the function
\[\varphi : \mathbb{Z} \rightarrow G ,\quad n \mapsto s^n \]
is a homomorphism. Deduce from this that if \(G\) is finite, then \(\operatorname{Ker}(\varphi )\) is nontrivial and therefore there exists a positive integer \(m\) such that \(s^m = e,\) where \(e\) is the identity element of \(G.\)
Solution. For any integers \(m\) and \(n,\) \[\varphi(m+n) = s^{m+n} = s^m s^n = \varphi(m) \varphi(n),\] which shows that \(\varphi\) is a homomorphism.
If \(s=e,\) then the kernel of \(\varphi\) is \(\mathbb{Z}\) and \(s^1 = e.\) If \(s\ne e,\) then the set \[S = \left\{ s^n \,\vert\, n \in \mathbb{Z} \right\}\] must contain \(e = s^0.\) Now consider the enumeration of elements: \[s^1 ,\, s^2 ,\, s^3,\, \cdots .\] Since \(S\) has only finite number of elements, there must be two different positive integers \(i\) and \(j\) such that \(s^i = s^j .\) Taking \(m = \lvert i-j \rvert > 0,\) we have \(s^m = e.\)
Problem 2.12
Use the previous problem and Proposition 2.6 to show that for each element \(s\) of a group \(G,\) the subset
\[\langle s \rangle = \left\{ s^n \,\vert\, n\in\mathbb{Z} \right\}\]
is a subgroup of \(G.\) This is called the cyclic subgroup generated by \(s\).
Solution. Let's check the conditions for \(\langle s \rangle\) to be a group.
- \(e = s^0 \in \langle s \rangle .\)
- If \(s^m\) and \(s^n\) belong to \(\langle s \rangle ,\) then \(s^m s^n = s^{m+n} \in \langle s \rangle .\)
- If \(s^n\) belongs to \(\langle s \rangle,\) then \(s^{-n}\) is the inverse element in \(\langle s \rangle .\)
Problem 2.13
Show that if \(H\) is a subgroup of \(G\) and \(s\in H,\) then \(\langle s \rangle \subseteq H.\) This means that \(\langle s \rangle\) is the smallest subgroup of \(G\) that contains \(s.\)
Solution. First, \(H\) must contain \(e = s^0 .\) Next, since \(H\) is closed under the group operation, \(s^n \in H\) for all positive integers \(n.\) Finally, since \(s^{-n}\) is the inverse element of \(s^n ,\) \(s^{-n} \in H\) for all positive integers \(n.\) Therefore \(H\) contains all the elements of \(\langle s \rangle .\)
Problem 2.14
Show that if a subgroup \(H\) of \(\langle \mathbb{Z}_4 ,\, + \rangle ,\) the additive group of integers modulo \(4,\) contains either \(1\) or \(3,\) then in fact \(H = \mathbb{Z}_4 .\)
Solution. In \(\mathbb{Z}_4 ,\) we have \[1+1 =2 ,\,\, 2+1 = 3 ,\,\, 3+1 = 0\] and \[3+3 = 2,\,\, 2+3 = 1 ,\,\, 1+3 = 0.\] Therefore each of \(1\) and \(3\) generates whole \(\mathbb{Z}_4 .\)
Problem 2.15
Find all subgroups of \(\langle \mathbb{Z}_5 ,\, + \rangle ,\) the additive group of integers modulo \(5.\)
Solution. Each nonzero element of \(\mathbb{Z}_5\) generates \(\mathbb{Z}_5 .\) Therefore \(\left\{ 0 \right\}\) and \(\mathbb{Z}_5\) are all the subgroups.
Problem 2.16
Let \(\varphi_1 ,\) \(\varphi_2 : \mathbb{Z}\rightarrow G\) be homomorphisms from the additive group \(\mathbb{Z}\) to an arbitrary group \(G.\) Show that if \(\varphi_1 (1) = \varphi_2 (1),\) then \(\varphi_1 = \varphi_2 .\) In other words, a group homomorphism from \(\mathbb{Z}\) into any group is completely determined by its action on \(1.\)
Solution. First, it is trivial that \(\varphi_1 (0) = e = \varphi_2 (0).\) Next, use mathematical induction for \(n\) to prove that \(\varphi_1 (n) = \varphi_2 (n),\) where \(n\) is any natural number. Finally, we have \[\varphi_1 (-n) = - \varphi_1 (n) = -\varphi_2 (n) = \varphi_2 (-n) \]for a natural number \(n.\)
Problem 2.17
Prove that a permutation and its inverse have the same sign.
Solution. Since the sign map is a homomorphism, we have \[\sigma (\pi ^{-1} ) = (\sigma (\pi ))^{-1}\]for a permutation \(\pi .\) But \(\sigma\) assumes only \(\pm 1\) and it completes the proof.
Problem 2.18
Let \(A_n\) denote the set of all even permutations in \(S_n ,\) that is, permutations with sign \(+1.\) Show that \(A_n\) is a subgroup of \(S_n .\)
Solution. The sign map \(\sigma : S_n \rightarrow \left\{ -1 ,\, 1 \right\}\) is a homomorphism and \(A_n\) is the kernel of the sign map. Therefore \(A_n\) is a subgroup of \(S_n .\)
Problem 2.19
Let \(G\) be a group. For \(s\in G,\) define \(L_s : G \rightarrow G\) by \(L_s (t) = st\) for all \(t\in G.\) \(L_s\) is thus left multiplication (or, more properly, left translation) by \(s.\)
- Let \(\operatorname{Sym}(G)\) denote the set of all bijections from \(G\) to itself, that is, all permutations of \(G.\) Show that for each \(s\in G,\) \(L_s \in \operatorname{Sym}(G).\)
- Show that the mapping\[\Lambda : G \rightarrow \operatorname{Sym}(G) ,\quad s \mapsto L_s\] is a homomorphism of groups. This amounts to showing that \(L_{st} = L_s \circ L_t .\)
- Show that \(\Lambda\) is, moreover, injective. Conclude that every group is isomorphic to a subgroup of a permutation group. This result is called Cayley's Theorem.
Solution.
- For any \(x\in G,\) \[L_s (s^{-1}x) = s(s^{-1})x = x,\] which shows that \(L_s\) is surjective. If \(L_c (x) = L_c (y)\) for \(x,\) \(y\in G,\) then \(cx=cy\) and \(x=y,\) which shows that \(L_s\) is injective. Therefore \(L_s\) is bijective and \(L_s\) belongs to \(\operatorname{Sym}(G).\)
- For any \(x\in G,\) \[L_{st}(x) = stx = s L_t (x) = L_s (L_t (x)) = (L_s \circ L_t )(x),\] that is, \(L_{st} = L_s \circ L_t .\) Therefore \[\Lambda(st) = L_{st} = L_s \circ L_t = \Lambda(s) \Lambda(t),\] which shows that \(\Lambda\) is a group-homomorphism.
- Suppose \(\Lambda(x) =\Lambda(y)\) then \(L_x = L_y \) and \[x = L_x (e) = L_y (e) = y,\]which shows that \(\Lambda\) is injective.
Problem 2.20
Let \(A\) be a ring. Show that \(A\) is commutative if and only if the following identity holds:
\[(a+b)^2 = a^2 + 2ab + b^2 .\tag{*}\]
Solution. If \(A\) is commutative, then (*) holds. Now we prove the converse. Let (*) holds for all \(a\) and \(b.\) Expanding LHS of (*) and substitute \(ab + ab\) into \(2ab,\) we have \[a^2 + ab + ba + b^2 = a^2 + ab + ab + b^2 .\] Cancellation law gives that \(ba = ab,\) which shows the commutativity.
Problem 2.21
Give an example of a commutative ring \(A\) such that neither \(a\) nor \(b\) is \(0,\) but \(ab=0.\) In this case we say \(a\) and \(b\) are zero divisors.
Solution. Take \(A = \mathbb{Z}_6\) and \(a = 2,\) \(b=3 .\)
Problem 2.22
Show that a field can never have zero divisors; that is, if \(ab=0,\) then either \(a\) or \(b\) is itself equal to \(0.\)
Solution. Suppose \(ab =0\) but \(a \ne 0.\) Then \(b = a^{-1}(ab) = a^{-1}0 = 0\) and we have \(b=0.\)
Problem 2.23
Write out both Cayley tables (one for addition, and one for multiplication) for \(\mathbb{F}_5 .\)
Solution.
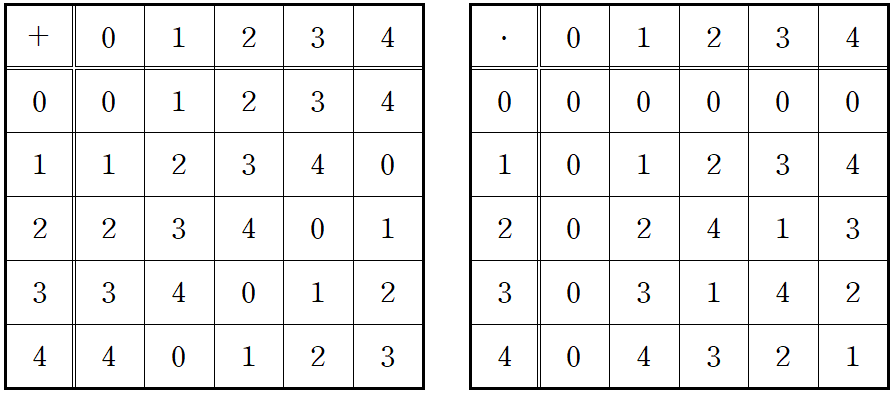
Problem 2.24
Write out both Cayley tables for \(\mathbb{Z}_6,\) the ring of integers modulo \(6.\) Show that this ring is not a field.
Solution.
 This ring has zero divisors \(2\) and \(3,\) therefore this ring is not a field.
This ring has zero divisors \(2\) and \(3,\) therefore this ring is not a field.
Problem 2.25
More generally show that \(\mathbb{Z}_n\) is not a field whenever \(n\) is not a prime number.
Solution. Since \(n\) is not a prime number, there exist positive integers \(p\) and \(q\) such that \(n=pq\) and \(p < n ,\) \(q < n.\) Then \(p\) and \(q\) are zero divisors of \(\mathbb{Z}_n,\) which shows that \(\mathbb{Z}_n\) is not a field.
(In fact, \(\mathbb{Z}_n\) is a field if and only if \(n\) is a prime number.)
Problem 2.26
A commutative ring without zero divisors is called an integral domain. Show that a commutative ring \(A\) is an integral domain if and only if we have the cancellation law
\[ab =ac \,\, \Rightarrow \,\, b=c \tag{*}\]
for all \(a,\,b,\,c \in A ,\) \(a \ne 0 .\) Use this result and the Pigeonhole Principle to show that every finite integral domain is a field.
Solution. Suppose (*) holds. If \(a\) and \(b\) were zero divisors, from \(ab = 0 = a0\) we have \(b=0,\) which is a contradiction. Thus \(A\) has no zero divisors. Conversely, suppose that \(A\) is an integral domain. If \(a \ne 0,\) then \(a^{-1}\) must be in \(A\), and from \(ab = ac\) we have \[b = a^{-1}(ab) = a^{-1}(ac) = c,\] which proves the cancellation law.
Now we prove that every finite integral domain is a field. Suppose \(D\) be a finite integral domain, consisting of the elements \[0 ,\,1 ,\, a_1 ,\, a_2 ,\, \cdots ,\, a_n .\] If \(D\) consists of \(0\) and \(1\) only, the proof is done. Therefore, suppose that \(D\) has more than \(2\) elements, and take any \(a\in D\) such that \(a \ne 0\) nor \(a \ne 1.\) Consider the elements \[a1 ,\, aa_1 ,\, aa_2 ,\, \cdots ,\, aa_n .\tag{**}\] Note that none of these elements equals \(0,\) since if \(aa_i = 0 ,\) then \(a_i = 0.\) Furthermore, these elements are all distinct, since if \(aa_i = aa_j ,\) then \(a_i = a_j .\) Thus these elements are just an rearrangement of the elements \[1 ,\, a_1 ,\, a_2 ,\, \cdots ,\, a_n .\] Therefore one of the enumeration (**) is equals to \(1,\) say \(a1 = 1\) or \(aa_k = 1,\) which implies that \(a\) has the multiplicative inverse in \(D,\) that is, \(D\) is a field.
Problem 2.27
Construct a field of four elements.
Solution.
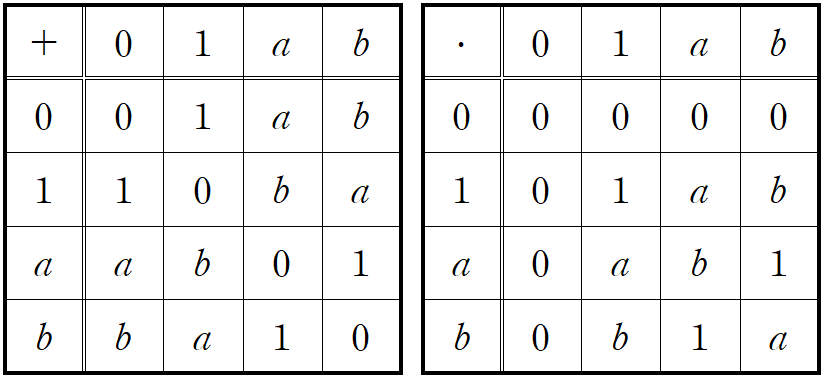
Additional Problems
The following two problems are not included in Valenza's book; They are not essential to study linear algebra, while they are frequently stated in abstract algebra.
Problem 2.28
Let \(m\) be a element of the ring \(\mathbb{Z}_n .\) Show that \(m\) is a zero divisor if and only if \(m\) divides \(n.\)
Solution. Suppose that \(d = \gcd (m,\,n ) \ne 1.\) Since \[m \left( \frac{n}{d} \right) = \left( \frac{m}{d} \right) n = 0 ,\] we have \(m(n/d)=0 .\) For \(m \ne 0\) nor \(n/d \ne 0\) in \(\mathbb{Z}_n ,\) \(m\) is a zero divisor of \(\mathbb{Z}_n .\)
Conversely, suppose that \(m\) is relative prime to \(n.\) If for \(s\in\mathbb{Z}_n\) we have \(ms = 0,\) then \(n\) divides \(ms.\) Since \(n\) is relatively prime to \(m,\) \(n\) divides \(s,\) so \(s=0\) in \(\mathbb{Z}_n .\)
Problem 2.29
Let \(p\) be a prime integer. Show that \(\mathbb{Z}_p\) is a field.
Solution. Since each nonzero element in \(\mathbb{Z}_p\) is not a zero divisor, we have by Problem 2.28 that \(\mathbb{Z}_p\) is an integral domain. Furthermore \(\mathbb{Z}_p\) consists of finite number of elements, we conclude by Problem 2.26 that \(\mathbb{Z}_p\) is a field.
