동형의 의미
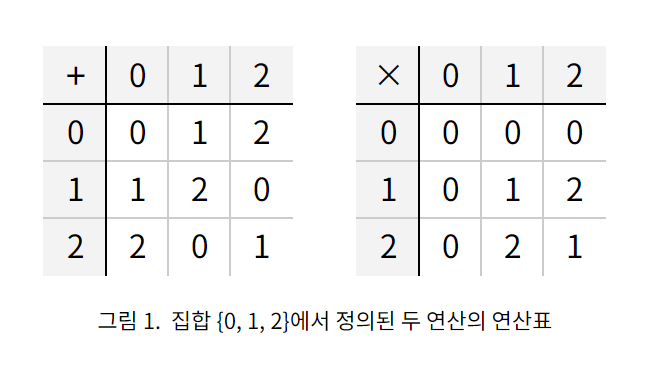
다음과 같은 집합 \(\mathbb{Z}_3\)을 생각해 보자. \[\mathbb{Z}_3 = \left\{ 0 ,\,\, 1,\,\,2 \right\}\] 이 집합 위에서 덧셈과 곱셈을 새롭게 정의해 보자. 즉 \(m\)과 \(n\)이 \(\mathbb{Z}_3\)의 원소일 때, 새로운 합 \(m+n\)을 \(m\)과 \(n\)의 합을 \(3\)으로 나눈 나머지로, 새로운 곱 \(mn\)을 \(m\)과 \(n\)의 곱을 \(3\)으로 나눈 나머지로 정의하자. 이와 같은 합과 곱을 표로 나타내면 다음 그림과 같다.
이와 같이 새롭게 정의된 합과 곱을 가진 집합 \(\mathbb{Z}_3\)은 체(field)의 조건을 모두 만족시킨다. 즉 \(\mathbb{Z}_3\)는 체이다.
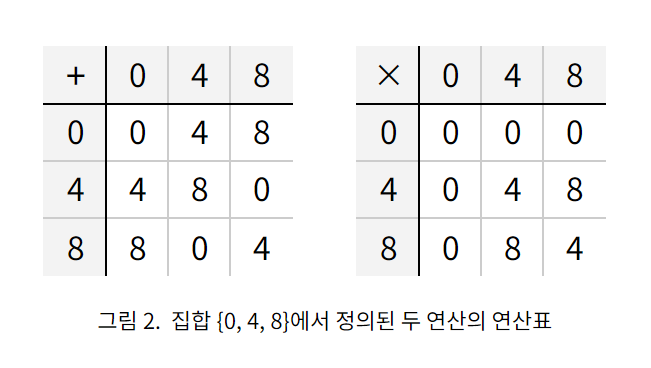
다음으로 다음과 같은 집합을 생각하자. \[F = \left\{ 0 ,\,\, 4 ,\,\, 8 \right\}\] 앞에서와 마찬가지로, 이 집합에 덧셈과 곱셈을 새롭게 정의해 보자. 즉 \(m\)과 \(n\)이 \(F\)의 원소일 때, 새로운 합 \(m+n\)을 \(m\)과 \(n\)의 합을 \(12\)로 나눈 나머지로, 새로운 곱 \(mn\)을 \(m\)과 \(n\)의 곱을 \(12\)로 나눈 나머지로 정의하자. 이와 같은 합과 곱을 표로 나타내면 다음 그림과 같다.
이와 같이 새롭게 정의된 합과 곱을 가진 집합 \(F\)는 체이다. 그런데 그림 1과 그림 2를 잘 살펴보면, 원소의 이름만 다를 뿐 각 집합에서 새롭게 정의한 덧셈과 곱셈에 의하여 구성되는 원소들 사이의 관계가 일치함을 알 수 있다. 즉 함수 \(\phi : \mathbb{Z} _3 \rightarrow F \)를 \[\begin{aligned} \phi ( 0 ) &= 0 , \\[6pt] \phi ( 1 ) &= 4 , \\[6pt] \phi ( 2 ) &= 8 \end{aligned}\] 이라고 정의하면 \(\phi\)는 일대일대응이며, \(\mathbb{Z} _3\)의 모든 원소 \(m,\) \(n\)에 대하여 다음을 만족시킨다. \[\begin{aligned} \phi (m+n) &= \phi (m) + \phi (n) ,\\[6pt] \phi (mn) &= \phi (m) \, \phi (n). \end{aligned}\] 위 두 등식의 좌변의 괄호 안에 있는 덧셈과 곱셈은 \(\mathbb{Z} _3\)에 정의된 연산이며, 등식의 우변에 있는 덧셈과 곱셈은 \(F\)에 정의된 연산이다. 즉 \(\phi\)는 \(\mathbb{Z} _3\)의 원소를 \(F\)의 원소에 하나씩 대응시키며, \(\mathbb{Z} _3\)의 구조(덧셈과 곱셈에 의하여 만들어진 원소들 사이의 관계)를 \(F\)의 구조에 대응시킨다. 이러한 관점에서 \(\phi\)는 \(\mathbb{Z} _3\)로부터 \(F\)로의 동형사상(isomorphism)이며, 두 체 \(\mathbb{Z} _3\)와 \(F\)는 서로 동형(isomorphic)이다.
두 집합 \(\mathbb{Z} _3\)와 \(F\)가 다른 원소를 가지고 있으므로, 두 집합은 같은 집합이 아니다. 그러나 두 집합이 가진 원소의 개수가 같고, 두 집합이 가지고 있는 구조가 동일하므로, “체의 성질을 연구한다”라는 관점에서는 두 체를 같은 것으로 보아도 무방하다.
벡터공간의 분류
이번에는 벡터공간의 동형성을 정의해 보자. “\(V\)가 체 \(F\) 위에서 정의된 벡터공간이다”라고 말할 때는 네 가지, 즉 스칼라의 집합 \(F,\) 벡터들의 집합 \(V,\) 벡터의 합, 스칼라 곱을 염두에 두는 것이다. 그러므로 “두 벡터공간이 서로 동형이다”라는 표현이 이와 같은 네 가지 구성 요소가 서로 일치함을 설명할 수 있도록 동형성을 정의해야 한다.
정의. (벡터공간의 동형성)
\(V\)와 \(W\)가 동일한 체 위에서 정의된 벡터공간이라고 하자. 만약 \(V\)와 \(W\) 사이에 일대일대응인 선형변환 \(T : V \rightarrow W\)가 존재하면 “\(V\)와 \(W\)는 서로 동형이다(isomorphic)”라고 말하고, 이와 같은 함수 \(T\)를 \(V\)로부터 \(W\)로의 동형사상(isomorphism)이라고 부른다.
두 벡터공간 \(V\)와 \(W\)가 서로 동형인 것을 기호로 ‘\(V \cong W\)’와 같이 나타낸다.
동형인 벡터공간의 예를 살펴보자. \(\mathbb{R}^4\)가 4차원 유클리드 벡터공간이고, \(\mathrm{Mat}_{2 \times 2} (\mathbb{R})\)가 \(2\times 2\)인 정사각형 실행렬로 이루어진 벡터공간이라고 하자.
만약 함수 \(\phi: \mathbb{R}^4 \rightarrow \mathrm{Mat}_{2 \times 2} (\mathbb{R})\)를 \[\phi : ( a_1 ,\,\, a_2 ,\,\, a_3 ,\,\, a_4 ) \,\mapsto \, \left[ \begin{array}{cc} a_1 & a_2 \\ a_3 & a_4 \end{array} \right] \] 와 같이 정의하면, \(\phi\)는 일대일대응인 선형변환이 된다. 즉 \(\phi\)는 동형사상이고, 두 벡터공간 \(\mathbb{R}^4\)와 \(\mathrm{Mat}_{2 \times 2} (\mathbb{R})\)는 서로 동형이다.
일반적으로 두 벡터공간이 동형인지 여부는 두 벡터공간의 차원을 비교하면 알 수 있다.
정리. (벡터공간의 분류)
\(V\)와 \(W\)가 동일한 체 위에서 정의된 벡터공간이라고 하자. 이때 \(V\)와 \(W\)가 서로 동형이기 위한 필요충분조건은 \(V\)의 차원과 \(W\)의 차원이 같은 것이다. 즉 \[V \cong W \quad \Longleftrightarrow \quad \dim (V) = \dim (W) \] 이다.
정리를 증명해 보자.
\(V \cong W \,\,\Rightarrow \,\, \dim(V) = \dim(W)\)의 증명
우선 \(V \cong W\)라고 가정하자. 동형의 정의에 의하여, 일대일대응인 선형변환 \[\phi : V \rightarrow W\] 가 존재한다. 또한 임의의 벡터공간은 기저를 가지므로 \(V\)의 기저가 존재한다. \(B\)를 \(V\)의 기저라고 하자. 집합 \(B ' \)을 다음과 같이 정의하자. \[B' = \left\{ \phi (\vecv ) \,\vert\, \vecv \in V \right\} .\] \(\phi\)가 일대일함수이므로 \(B ' \)은 \(B\)와 같은 수의 원소를 가진다. 이제 우리의 목표는 \(B ' \)이 \(W\)의 기저가 됨을 보이는 것이다.
\(B ' \)에 속하는 유한 개의 벡터 \[\vecw _1 ,\,\, \vecw_2 ,\,\, \cdots ,\,\, \vecw_k \] 를 생각하자. 그리고 이 벡터의 일차결합이 \(\veczero\)인 경우를 생각하자. 즉 다음 등식을 생각하자. \[\alpha_1 \,\vecw_1 + \alpha_2 \,\vecw_2 + \cdots + \alpha_k \, \vecw_k = \veczero.\] 여기서 각 \(\alpha_j \)는 스칼라이다. 좌변의 각 \(\vecw_j\)는 \(B ' \)의 원소이므로, \(\phi(\vecv _j ) = \vecw_j \)인 \(\vecv_j\)가 \(B\)에 존재한다. 즉 위 등식은 다음과 같이 쓸 수 있다. \[\alpha_1 \,\phi( \vecv_1 ) + \alpha_2 \,\phi( \vecv_2 ) + \cdots + \alpha_k \, \phi( \vecv_k ) = \veczero.\] \(\phi\)가 선형변환이므로, 위 등식은 다음과 같이 쓸 수 있다. \[\phi ( \alpha_1 \, \vecv_1 + \alpha_2 \, \vecv_2 + \cdots + \alpha_k \,\vecv_k ) = \veczero .\] \(\phi\)가 일대일대응이므로, 위 등식은 다음과 같다. \[\alpha_1 \, \vecv_1 + \alpha_2 \, \vecv_2 + \cdots + \alpha_k \,\vecv_k = \veczero .\] 그런데 \(\vecv_1 ,\) \(\vecv_2 ,\) \(\cdots ,\) \(\vecv_k\)가 일차독립이므로 \[\alpha_1 = \alpha_2 = \cdots = \alpha_k = 0\] 이다. 그러므로 \(B ' \)은 일차독립이다.
다음으로 \(B '\)이 \(W\)를 생성함을 보이자. \(W\)에 속하는 임의의 벡터 \(\vecw\)가 주어졌다고 하자. \(\phi\)가 위로의 함수이므로 \(\phi (\vecv ) = \vecw\)인 벡터 \(\vecv\)가 \(V\)에 존재한다. \(B\)가 \(V\)의 기저이므로, \(B\)의 원소 \(\vecv_1 ,\) \(\vecv_2 ,\) \(\cdots ,\) \(\vecv_ p\)와 스칼라 \(\beta_1 ,\) \(\beta_2 ,\) \(\cdots ,\) \(\beta_p \)가 존재하여 다음을 만족시킨다. \[\vecv = \beta_1 \, \vecv_1 + \beta_2 \,\vecv_2 + \cdots + \beta_p \,\vecv_p .\] \(j=1,\,\,2,\,\,\cdots,\,\,p\)에 대하여 \(\vecw_j = \phi(\vecv_j )\)라고 하자. 그러면 \(\vecw_j\)는 \(B ' \)의 원소이다. 또한 다음이 성립한다. \[\begin{aligned} \vecw &= \phi( \vecv ) \\[6pt] &= \phi( \beta_1 \, \vecv_1 + \beta_2 \,\vecv_2 + \cdots + \beta_p \,\vecv_p ) \\[6pt] &= \beta_1 \, \phi( \vecv_1 ) + \beta_2 \, \phi ( \vecv_2 ) + \cdots + \beta_p \, \phi ( \vecv_p ) \\[6pt] &= \beta_1 \, \vecw_1 + \beta_2 \,\vecw_2 + \cdots + \beta_p \,\vecw_p . \end{aligned}\] 즉 \(W\)에 속하는 임의의 벡터는 \(B ' \)의 벡터의 일차결합으로 표현된다. 그러므로 \(B ' \)은 \(W\)를 생성한다.
결론적으로 \(B ' \)은 \(W\)의 기저이다. \(V\)의 기저와 \(W\)의 기저가 같은 수의 원소를 가지므로, \(V\)의 차원과 \(W\)의 차원이 같다.
\(\dim(V) = \dim(W) \,\,\Rightarrow \,\, V \cong W\)의 증명
이제 역을 증명하자. 즉 \(V\)와 \(W\)의 차원이 같다고 가정하자. 그리고 \(B\)와 \(B ' \)을 각각 \(V\)와 \(W\)의 기저라고 하자. 그러면 \(B\)와 \(B'\)은 원소의 수가 같은 집합이다. 그러므로 일대일대응 \(T : B \rightarrow B ' \)이 존재한다. \(V\)의 기저의 모든 원소에 대하여 \(T\)의 함숫값이 정의되었으므로, 선형 확장 정리에 의하여 \(T\)의 정의역을 \(V\)로 확장하여 선형변환 \(T : V \rightarrow W\)를 만들 수 있다. 이렇게 만든 선형변환 \(T\)가 일대일대응임을 보이면 \(T\)는 동형사상이 된다.
표기를 편하게 하기 위해 \[\begin{aligned} B &= \left\{ \vecv_j \,\vert\, j\in J \right\} , \\[6pt] \vecw_j &= \phi (\vecv_j ) \text{ for } j \in J, \\[6pt] B ' &= \left\{ \vecw_j \,\vert\, j\in J \right\} \end{aligned}\] 라고 하자.
\(T\)가 일대일함수임을 보이자. \(\vecu\)와 \(\vecv\)가 \(V\)의 벡터이고 \(\vecu \ne \vecv \)라고 가정하자. \(\vecu\)와 \(\vecv\)를 \(B\)의 일차결합으로 표현하는 데에 사용되는 \(B\)의 원소 전체를 \(\vecv_1 ,\) \(\vecv_2 ,\) \(\cdots ,\) \(\vecv_n\)이라고 하자. 그러면 \(\vecu\)와 \(\vecv\)는 각각 다음과 같이 표현된다. \[\begin{aligned} \vecu &= \alpha_1 \,\vecv_1 + \alpha_2 \,\vecv_2 + \cdots + \alpha_n \,\vecv_n , \\[6pt] \vecv &= \beta_1 \,\vecv_1 + \beta_2 \,\vecv_2 + \cdots + \beta_n \,\vecv_n . \end{aligned}\] 여기서 두 등식의 좌변에 있는 모든 \(\alpha_j\)와 \(\beta_j\)는 스칼라이다. \(\phi\)가 선형변환이므로 \(T(\vecv )\)와 \(T(\vecu )\)는 각각 \(B ' \)의 원소의 일차결합으로 표현된다: \[\begin{aligned} T(\vecv ) &= T( \alpha_1 \,\vecv_1 + \alpha_2 \,\vecv_2 + \cdots + \alpha_n \,\vecv_n ) \\[6pt] &= \alpha_1 \, T( \vecv_1 ) + \alpha_2 \, T( \vecv_2 ) + \cdots + \alpha_n \, T( \vecv_n ) \\[6pt] &= \alpha_1 \,\vecw_1 + \alpha_2 \,\vecw_2 + \cdots + \alpha_n \,\vecw_n \,, \\[10pt] T(\vecu ) &= T( \beta_1 \,\vecu_1 + \beta_2 \,\vecu_2 + \cdots + \beta_n \,\vecu_n ) \\[6pt] &= \beta_1 \, T( \vecu_1 ) + \beta_2 \, T( \vecu_2 ) + \cdots + \beta_n \, T( \vecu_n ) \\[6pt] &= \beta_1 \,\vecw_1 + \beta_2 \,\vecw_2 + \cdots + \beta_n \,\vecw_n \,. \end{aligned}\] 한 벡터를 기저의 일차결합으로 표현하는 형태는 유일하하다. 그런데 \(\vecu \ne \vecv \)이므로 \(\alpha_p \ne \beta_p\)인 \(p\)가 존재한다. 그러므로 \(T(\vecv ) \ne T(\vecu )\)이다. 즉 \(T\)는 일대일함수이다.
다음으로 \(T\)가 위로의 함수임을 보이자. \(W\)의 벡터 \(\vecw\)가 임의로 주어졌다고 하자. \(B ' \)이 \(W\)의 기저이므로, \[\vecw = \lambda_1 \,\vecw_1 + \lambda_2 \, \vecw_2 + \cdots + \lambda_q \, \vecw_q\] 인 \(B '\)의 원소 \(\vecw_1 ,\) \(\vecw_2 ,\) \(\cdots ,\) \(\vecw_q \)와 스칼라 \(\lambda_1 ,\) \(\lambda_2 ,\) \(\cdots ,\) \(\lambda_q\)가 존재한다. \(V\)의 벡터 \(\vecv\)를 다음과 같이 정의하자. \[\vecv = \lambda_1 \,\vecv_1 + \lambda_2 \, \vecv_2 + \cdots + \lambda_q \, \vecv_q\] 그러면 \(T\)의 선형성에 의하여 다음이 성립한다. \[\begin{aligned} T(\vecv) &= T( \lambda_1 \,\vecv_1 + \lambda_2 \, \vecv_2 + \cdots + \lambda_q \, \vecv_q ) \\[6pt] &= \lambda_1 \, T( \vecv_1 ) + \lambda_2 \, T( \vecv_2 ) + \cdots + \lambda_q \, T( \vecv_q ) \\[6pt] &= \lambda_1 \,\vecw_1 + \lambda_2 \, \vecw_2 + \cdots + \lambda_q \, \vecw_q \\[6pt] &= \vecw . \end{aligned}\] 즉 \(T(\vecv) = \vecw\)인 벡터 \(\vecv\)가 \(V\)에 존재하므로, \(\vecw\)는 \(T\)의 치역에 속한다. 그러므로 \(T\)는 위로의 함수이다.
결론적으로 \(T : V \rightarrow W\)는 일대일대응인 선형변환이다. 그러므로 두 벡터공간 \(V\)와 \(W\)는 서로 동형이다.