평면에서 선적분과 이중적분의 관계를 설명하는 그린 정리가 있는 것처럼 공간에서도 선적분과 면적분의 관계를 설명하는 정리, 면적분과 삼중적분의 관계를 설명하는 정리가 있다. 이 포스트에서는 그린 정리를 3차원으로 확장한 적분 정리를 살펴본다.
내용 순서
미리 알아야 할 내용
회전벡터장
앞에서 그린 정리를 공부하면서 평면벡터장 \(\mathbf{F}(x,\,y) = M(x,\,y)\mathbf{i} + N(x,\,y)\mathbf{j}\)의 순환밀도가 다음과 같음을 살펴보았다. \[\frac{\partial N}{\partial x} - \frac{\partial M}{\partial y}.\tag{1.1}\] 이 값은 평면에서 유체의 흐름이 \(\mathbf{F}\)와 같을 때, 유체가 흐르는 지점 \((x,\,y)\)에 놓인 외륜(paddle wheel)이 얼마나 빠르게 회전하는지를 나타낸다. 이 값이 양수이면 외륜은 위에서 보았을 때 양의 방향(반시계방향)으로 회전하고, 이 값이 음수이면 외륜은 음의 방향으로 회전하며, 이 값이 \(0\)이면 외륜은 회전하지 않는다(그림 1).
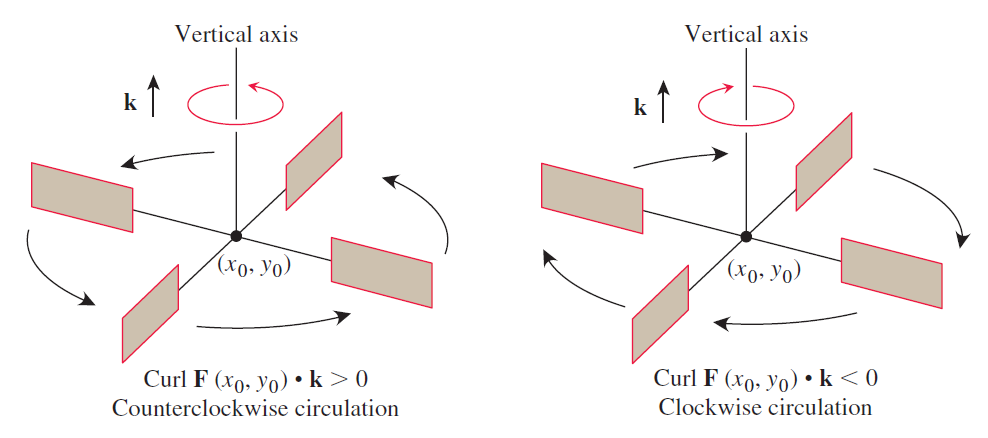
공간벡터장에 대해서도 이와 비슷한 정의를 도입할 수 있다. 공간벡터장 \[\mathbf{F} (x,\,y,\,z) = M(x,\,y,\,z)\mathbf{i} + N(x,\,y,\,z)\mathbf{j} + P(x,\,y,\,z)\mathbf{k}\]의 모든 성분이 모든 변수에 대하여 편미분 가능할 때, \(\mathbf{F}\)의 회전벡터장(curl)을 다음과 같이 정의한다. \[\curl \,\mathbf{F} = \left( \frac{\partial P}{\partial y} - \frac{\partial N}{\partial z} \right) \mathbf{i} + \left(\frac{\partial M}{\partial z} - \frac{\partial P}{\partial x}\right) \mathbf{j} + \left(\frac{\partial N}{\partial x} - \frac{\partial M}{\partial y}\right) \mathbf{k}.\tag{1.2}\] 위 식을 간단하게 다음과 같이 나타낸다. \[\curl \,\mathbf{F} = \nabla \times \mathbf{F} .\tag{1.3}\] 평면벡터장의 순환밀도가 스칼라인 것과는 달리 공간벡터장의 회전벡터장은 벡터이다. 특히 (2)의 \(\mathbf{k}\) 성분은 (1)과 같다. 즉 \[(\curl \,\mathbf{F})\cdot \mathbf{k} = \frac{\partial N}{\partial x} - \frac{\partial M}{\partial y}\tag{1.4}\] 이다. 이러한 관점에서 순환밀도를 ‘회전벡터장의 \(\mathbf{k}\) 성분’이라고 부르기도 한다.
보기 1 벡터장 \(\mathbf{F} = (x^2 - z)\mathbf{i} + xe^z\,\mathbf{j} + xy\,\mathbf{k}\)의 회전벡터장을 구해 보자. \[\begin{align} \curl \,\mathbf{F} &= \nabla \times \mathbf{F} \\[5pt] &= \left\lvert \begin{array}{ccc} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ \frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\ x^2 -z & xe^z & xy \end{array} \right\vert \\[5pt] &= (x-xe^z )\mathbf{i} - (y+1)\mathbf{j} + (e^z-0)\mathbf{k} \\[5pt] &= x(1-e^z)\mathbf{i} - (y+1)\mathbf{j} + e^z\,\mathbf{k}. \end{align}\]
회전벡터장은 크기와 방향을 가진다. 이를 바탕으로 회전벡터장의 의미를 물리적으로 설명할 수 있다.

\(\mathbf{F}\)가 공간에서 유체의 흐름을 나타내는 공간벡터장이라고 하자. 고정된 지점 \((x,\,y,\,z)\)에 외륜을 두었을 때, 외륜이 \(\mathbf{F}\)의 영향을 받아 회전하는 속도는 외륜의 축의 방향에 의하여 정된다. 만약 \(\nabla \times \mathbf{F} \ne \mathbf{0}\)이라면, 외륜의 축이 \(\nabla \times \mathbf{F}\)와 평행할 때 외륜이 가장 빠르게 회전하며, 이때 외륜의 회전 방향은 \(\nabla \times \mathbf{F}\)의 방향을 기준으로 하는 오른손 법칙을 따르는 방향이다(그림 2).
특히, \(\mathbf{n}\)이 단위벡터일 때 \((\nabla \times \mathbf{F})\cdot\mathbf{n}\)은 점 \((x,\,y,\,z)\)에 놓여 있고 축의 방향이 \(\mathbf{n}\)과 일치하는 외륜이 얼마나 빠르게 회전하는지를 나타낸다.
스토크스 정리
그린 정리는 평면영역의 경계선에서의 선적분과 평면영역에서의 중적분의 관계를 설명해 준다. 즉 평면곡선 \(C\)가 조각마다 매끄러우며 닫혀 있는 단순곡선이고, \(C\)에 의하여 둘러싸인 영역을 \(R\)라고 할 때, \(C\)와 \(R\)를 포함하는 열린 영역에서 연속인 편도함수를 갖는 평면벡터장 \(\mathbf{F} = M\,\mathbf{i} + N\,\mathbf{j}\)에 대하여 다음이 성립한다. \[\oint_C M\,dx + N\,dy = \iint_R \left( \frac{\partial N}{\partial x} - \frac{\partial M}{\partial y} \right) dx\,dy .\tag{2.1}\] 이 식의 좌변은 \(C\)를 따라 흐르는 \(\mathbf{F}\)의 반시계방향 순환이며, 우변은 영역 \(R\)에서 순환밀도 \((\curl\,\mathbf{F})\cdot\mathbf{k}\)의 이중적분이다.
이러한 정리를 3차원 공간으로 확장할 수 있다. 이것을 위해서 먼저 ‘다양체경계’의 개념을 도입해야 한다. 다음과 같은 집합을 생각해 보자. \[S_1 = \left\{ (x,\,y,\,z) \,\vert\, x^2 + y^2 \le 1 ,\,\, z=0 \right\}\tag{2.2}\] 집합 \(S_1\)은 \(\mathbb{R}^3\)의 부분집합이며, 이 집합의 모든 점은 자기 자신의 경계점이다. 하지만 \(S_1\)을 \(xy\) 평면에 놓인 조각이라 생각하면 이 집합의 경계를 원 \[C = \left\{ (x,\,y) \,\vert\, x^2 + y^2 = 1\right\}\tag{2.3}\] 이라고 생각할 수 있다. 이때 \(C\)를 \(S_1\)의 다양체경계(manifold boundary)라고 부른다. 다양체경계와 구분하기 위하여 기존의 경계를 위상경계(topological boundary)라고 부른다.
이해를 돕기 위해 다양체경계의 예를 하나 더 살펴보자. 다음과 같은 반구면 \(S_2\)를 생각하자. \[S_2 = \left\{ (x,\,y,\,z) \,\vert\, x^2 + y^2 + z^2 = 1 ,\,\, z \ge 0 \right\}\tag{2.4}\] \(S_2\)의 위상경계는 자기 자신이다. 그러나 \(S_2\)의 다양체경계는 (2.2)의 다양체경계와 같은 (2.3)의 원 \(C\)이다.
이제 그린 정리를 3차원 공간으로 확장한 정리를 살펴보자. 여기서는 증명은 하지 않고 식의 의미를 살펴보겠다. 증명이 궁금하면 미적분학 교재를 참고하기 바란다.
정리 1. (Stokes 정리) \(S\)가 공간에 놓인 곡면이며 조각마다 매끄럽고 방향을 가진 곡면이라고 하자. 그리고 \(S\)의 다양체경계 \(C\)가 매끄러운 곡선이라고 하자(그림 3).

벡터장 \(\mathbf{F} = M\,\mathbf{i} + N\,\mathbf{j} + P\,\mathbf{k}\)가 \(S\)를 포함하는 한 열린 영역에서 정의되어 있고, 그 영역에서 연속인 편도함수를 가지면 다음이 성립한다. \[\oint_C \mathbf{F} \cdot d\mathbf{r} = \iint_S (\nabla \times \mathbf{F})\cdot \mathbf{n} \,d\sigma .\tag{2.5}\] 이 등식의 좌변은 곡면의 단위법선벡터 \(\mathbf{n}\)에 관하여 오른손 법칙에 따라 반시계방향으로 \(C\)를 따라 회전하는 \(\mathbf{F}\)의 순환이며, 우변은 곡면 \(S\) 위에서 순환밀도 \((\nabla \times \mathbf{F})\cdot \mathbf{n}\)의 적분이다.
스토크스 정리와 그린 정리의 관계를 살펴 보자.
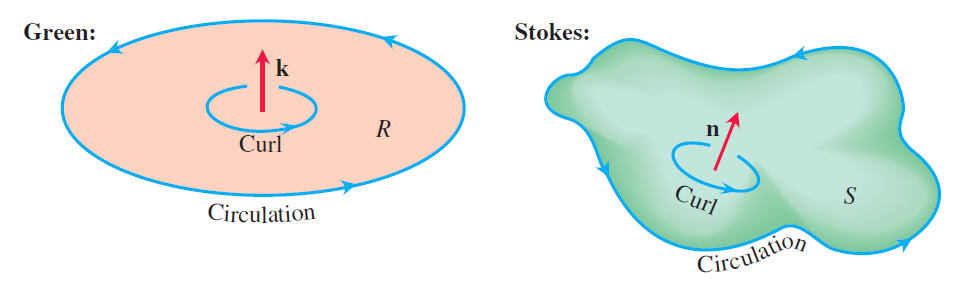
\(S\)가 \(xy\) 평면에 놓인 영역이고 그린 정리를 적용할 수 있는 조건을 만족시킨다고 하자. 이때 \(d\sigma = dx\,dy\)이고 (1.4)에 의하여 \[(\nabla \times \mathbf{F})\cdot\mathbf{n} = (\nabla \times \mathbf{F})\cdot\mathbf{k} = \frac{\partial N}{\partial x} - \frac{\partial M}{\partial y}\tag{2.6}\] 이므로 스토크스 정리의 식 (2.5)에 의하여 다음을 얻는다. \[\oint_C \mathbf{F} \cdot d\mathbf{r} = \iint_S (\nabla \times \mathbf{F})\cdot \mathbf{n} \,d\sigma =\iint_S \left( \frac{\partial N}{\partial x} - \frac{\partial M}{\partial y}\right) dx\,dy.\tag{2.7}\] 이것은 곧 그린 정리와 같다.
보기 2. 상반구면 \[S = \left\{ (x,\,y,\,z) \,\vert\, x^2 + y^2 + z^2 = 9 ,\,\, z\ge 0\right\}\tag{2.8}\] 에 원점으로부터 멀어지는 방향(\(z\)축의 양의 방향에 가까운 방향)으로 단위법선벡터 \(\mathbf{n}\)이 주어져 있고, \(\mathbf{n}\)을 기준으로 오른손 법칙을 따라 양의 방향으로 회전이 주어져 있으며 \(S\)의 다양체경계에 해당하는 원 \[C = \left\{(x,\,y) \,\vert\, x^2 + y^2 = 9\right\}\tag{2.9}\] 에 \(S\)의 회전방향과 일치하는 방향이 주어져 있다고 하자(그림 5).
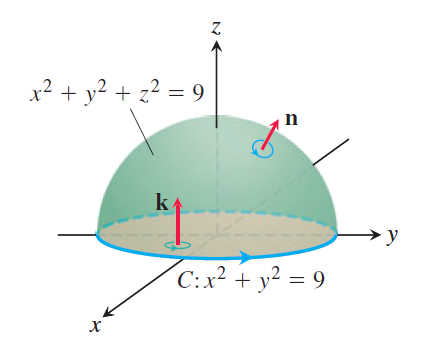
벡터장 \(\mathbf{F} = y\,\mathbf{i} - x\,\mathbf{j}\)에 대하여 스토크스 정리를 확인해 보자.
먼저 \(C\)를 따르는 선적분, 즉 (2.5)의 좌변을 계산해 보자. 원 \(C\)를 매개화하면 \[\mathbf{r}(\theta) = (3\cos\theta) \mathbf{i} + (3\sin\theta )\mathbf{j} ,\,\, 0\le \theta\le 2\pi\] 이므로 다음을 얻는다. \[\begin{align} d\mathbf{r} &= (-3\sin\theta \,d\theta )\mathbf{i} + (3\cos\theta \,d\theta )\mathbf{j}, \\[5pt] \mathbf{F} &= y\,\mathbf{i} - x\,\mathbf{j} = (3\sin\theta )\mathbf{i} - (3\cos\theta )\mathbf{j}, \\[5pt] \mathbf{F} \cdot d\mathbf{r} &= -9 \sin^2 \theta \,d\theta - 9\cos^2 \theta \,d\theta =-9 \,d\theta, \\[5pt] \oint_C \mathbf{F} \cdot d\mathbf{r} &= \int_0^{2\pi} (-9)d\theta = - 18 \pi . \tag{2.10} \end{align}\] 다음으로 \(S\) 위에서 순환밀도의 적분, 즉 (2.5)의 우변을 계산해 보자. 곡면 \(S\)를 \[f(x,\,y,\,z) = x^2 + y^2 + z^2 = 9\] 로 나타내면 \[\begin{align} \lvert \nabla f \rvert &= \lvert 2x\,\mathbf{i} + 2y\,\mathbf{j} + 2z\,\mathbf{k} \rvert = 2\sqrt{x^2 + y^2 + z^2} = 6 ,\\[5pt] \lvert \nabla f \cdot \mathbf{k} \rvert &= \lvert 2z \rvert = 2z ,\\[5pt] d\sigma &= \frac{\lvert \nabla f \rvert}{\lvert \nabla f \cdot \mathbf{k} \rvert} dA = \frac{3}{z} dA \end{align}\] 이다. 여기서 \(dA\)는 \(xy\) 평면 위의 원판 \(x^2 + y^2 \le 9\)의 미분소를 나타낸다. 그러므로 다음을 얻는다. \[\begin{align} \nabla \times \mathbf{F} &= (0-0) \mathbf{i} + (0-0)\mathbf{j} + (-1-1)\mathbf{k} = -2\mathbf{k} ,\\[5pt] \mathbf{n} &= \frac{x\,\mathbf{i} + y\,\mathbf{j} + z\,\mathbf{k}}{\sqrt{x^2 + y^2 + z^2}} = \frac{x\,\mathbf{i} + y\,\mathbf{j} + z\,\mathbf{k}}{3},\\[5pt] d\sigma &= \frac{3}{z} dA ,\\[5pt] (\nabla \times \mathbf{F}) \cdot \mathbf{n} &= - \frac{2z}{3} \frac{3}{z} dA = -2\,dA,\\[5pt] \iint_S (\nabla \times \mathbf{F} )\cdot \mathbf{n} \,d\sigma &= \iint_{x^2 +y^2 \le 9} -2 \,dA = -18 \pi . \tag{2.11} \end{align}\] 계산 결과 (2.10)과 (2.11)을 비교하면 일치한다.
보기 3. 보기 2의 벡터장 \(\mathbf{F} = y\,\mathbf{i} - x\,\mathbf{j}\)가 \(xy\) 평면의 원판 \(x^2 + y^2 \le 9\)를 포함하는 영역에서 연속인 편도함수를 가지므로, 보기 2의 적분은 그린 정리를 이용하여 더 쉽게 계산할 수 있다. \(xy\) 평면에서 (2.9)의 원 \(C\)를 둘레로 갖는 원판 영역을 \(A\)라고 하자.

그러면 \(A\) 위에서 \(d\sigma = dA\)이고 \(\mathbf{n} = \mathbf{k}\)이므로 \[(\nabla \times \mathbf{F})\cdot \mathbf{n} \,d\sigma = -2 \,\mathbf{k} \cdot \mathbf{k} \,dA = -2 \,dA\] 이다. 그러므로 그린 정리에 의하여 \[\oint_C \mathbf{F} \cdot d\mathbf{r} = \iint_A ( \nabla \times \mathbf{F})\cdot \mathbf{k} \,dA = \iint_A (-2)dA = -18 \pi\] 이다.
스토크스 정리의 응용
스토크스 정리를 이용하면 앞에서 생략하였던 보존적 벡터장의 성질의 증명을 할 수 있다. 먼저 다음 등식이 성립함을 확인하자.
등식 (3.1)은 정의에 따라 계산하면 바로 얻을 수 있다. 즉 \[\begin{align} \curl \,\grad f &= \nabla \times \nabla f \\[5pt] &= (f_{zy} - f_{yz})\mathbf{i} - (f_{zx} - f_{xz})\mathbf{j} + (f_{yx} - f_{xy})\mathbf{k} \tag{3.2} \\[5pt] \end{align}\] 이다. 그런데 클래로의 정리에 의하여 혼합편도함수의 편미분 순서를 바꾸어도 결과가 동일하므로, (3.2)의 마지막 식의 각 성분은 모두 \(0\)이다. 그러므로 (3.1)이 성립한다.
여기서 멈추지 말고 (3.2)의 식을 잘 살펴보자. 만약 \[\mathbf{F} = M\,\mathbf{i} + N\,\mathbf{j} + P\,\mathbf{k} = \nabla f\tag{3.3}\] 라면, (3.2)의 우변의 각 성분이 \(0\)이라는 것은 다음과 같이 나타낼 수 있다. \[\frac{\partial P}{\partial y} = \frac{\partial N}{\partial z} ,\,\, \frac{\partial M}{\partial z} = \frac{\partial P}{\partial x} ,\,\, \frac{\partial N}{\partial x} = \frac{\partial M}{\partial y} .\tag{3.4}\] 이것은 \(\mathbf{F}\)가 보존적 벡터장인지를 판별하는 성분 판정법의 식과 일치한다. 16.6절에서 \(\mathbf{F}\)가 보존적 벡터장일 때 (3.4)가 성립한다는 사실만 증명하고 그 역은 증명하지 않았다. 이제 그 역을 증명하자.
단순연결영역 \(D\)에서 (3.4)가 성립한다고 가정하자. 그러면 \[\nabla \times \mathbf{F} = \mathbf{0}\tag{3.5}\] 이다. \(C\)가 \(D\)에 포함되고 조각마다 매끄러운 닫힌 단순곡선이라고 하자. 그리고 \(C\)를 다양체경계로 갖고 \(D\)에 포함되며 조각마다 매끄러운 양면곡면 하나를 택하여 \(S\)라고 하자. \(S\)의 두 방향 중 하나를 임의로 택하고 그 방향과 일치하는 \(S\) 위의 단위법선벡터를 \(\mathbf{n}\)이라 하며, \(\mathbf{n}\)을 기준으로 오른손 법칙을 따르는 회전방향과 일치하도록 \(C\)에 방향이 주어졌다고 하자. 그러면 스토크스 정리에 의하여 다음을 얻는다. \[\oint_C \mathbf{F} \cdot d\mathbf{r} = \iint_S (\nabla \times \mathbf{F}) \cdot \mathbf{n} \,d\sigma = \iint_S \mathbf{0} \cdot \mathbf{n} \,d\sigma = 0.\] 여기서 \(C\)가 \(D\)에 포함되고 조각마다 매끄러운 ‘임의의’ 닫힌 단순곡선이므로 \(\mathbf{F}\)는 \(R\)에서 보존적이다.
발산 정리
그린 정리를 3차원 공간으로 확장한 또 다른 정리를 살펴보자. 평면곡선 \(C\)가 조각마다 매끄러우며 닫혀 있는 단순곡선이고 \(C\)에 의하여 둘러싸인 영역을 \(R\)라고 할 때, \(C\)와 \(R\)를 포함하는 열린 영역에서 연속인 편도함수를 갖는 평면벡터장 \(\mathbf{F} = M\,\mathbf{i} + N \,\mathbf{j}\)에 대하여 다음이 성립한다. \[\oint_C M\,dy - N\,dx = \iint_R \left( \frac{\partial M}{\partial x} + \frac{\partial N}{\partial y}\right) dx\,dy.\tag{4.1}\] 이 식의 좌변은 곡선 \(C\)의 바깥쪽으로 흘러 나가는 \(\mathbf{F}\)의 유출(flux)이며, 우변은 영역 \(R\)에서 유출밀도 \(\opdiv \,\mathbf{F}\)의 이중적분이다.
유체의 흐름을 이용하여 식 (4.1)을 설명할 수 있다. 평평한 지표면 바닥에서 물이 흘러나오고 있는데, 그 영역의 곡선 \(C\)에 해당하는 부분에 울타리를 쳐 두었다. \(C\) 안쪽 바닥면에서 단위시간동안 물이 얼마나 흘러나오는지 구하고 싶다면 (4.1)의 우변을 계산하면 된다. 그런데 이것은 단위시간동안 울타리 \(C\)를 넘어서 흘러나오는 물의 양을 구하면 되므로 (4.1)의 좌변을 계산하면 된다. 이러한 관점에서 (4.1)의 좌변과 우변은 같은 값을 가진다.
유출밀도 \(\opdiv\,\mathbf{F}\)는 통상적으로 ‘발산’이라는 이름으로 더 많이 불리므로, 여기서도 ‘발산’이라는 이름을 사용하겠다. 평면벡터장의 발산은 자연스럽게 공간벡터장으로 확장될 수 있다.

3차원 공간에서 정의되어 있고 모든 성분이 편도함수를 갖는 벡터장 \[\mathbf{F} = M\,\mathbf{i} + N\,\mathbf{j} + P\,\mathbf{k}\] 의 발산(divergence)을 다음과 같이 정의한다. \[\opdiv\,\mathbf{F} = \nabla \cdot \mathbf{F} = \frac{\partial M}{\partial x} + \frac{\partial N}{\partial y} + \frac{\partial P}{\partial z}.\tag{4.2}\] 유체의 흐름이 \(\mathbf{F}\)와 같을 때, \(\opdiv \,\mathbf{F} > 0\)이면 유체가 팽창하는 것이며, \(\opdiv \,\mathbf{F} < 0\)이면 유체가 압축되고 있는 것이다(그림 6).
그린 정리의 공식 (4.1)은 다음과 같이 자연스럽게 3차원 공간으로 확장된다. 스토크스 정리와 마찬가지로, 여기서는 증명은 하지 않고 식의 의미를 살펴보겠다.
정리 2. (발산 정리; Gauss 정리) \(S\)가 공간에 놓인 곡면이며 조각마다 매끄럽고 방향을 가진 닫힌곡면이라고 하자. 그리고 \(S\) 위에 바깥쪽을 향하는 단위법선벡터를 \(\mathbf{n}\)이라고 하자. \(S\)를 경계로 갖는 닫힌영역을 \(D\)라고 하면 다음이 성립한다. \[\iint_S \mathbf{F} \cdot \mathbf{n} \,d\sigma = \iiint_D \nabla \cdot \mathbf{F} \,dV . \tag{4.3}\] 이 등식의 좌변은 곡면 \(S\)를 통과하여 바깥쪽으로 나가는 벡터장 \(\mathbf{F}\)의 유출(flux)이며, 우변은 영역 \(D\)에서 유출밀도 \(\opdiv \,\mathbf{F}\)의 적분이다.
예를 통해 발산 정리를 확인해 보자.
보기 4. 반지름이 \(a > 0\)인 구면 \(x^2 + y^2 + z^2 = a^2\)에 바깥쪽을 향하는 방향이 주어진 곡면을 \(S\)라고 하자. 그리고 \(S\)에 의하여 둘러싸인 닫힌 영역을 \(D\)라고 하자. 즉 \(D\)는 \(x^2 + y^2 + z^2 \le a^2\)인 영역이다. 벡터장 \(\mathbf{F} = x\,\mathbf{i} + y\,\mathbf{j} + z\,\mathbf{k}\)에 대하여 발산 정리를 확인해 보자.
먼저 곡면 \(S\)를 통과하여 바깥쪽으로 나가는 \(\mathbf{F}\)의 유출, 즉 (4.3)의 좌변을 계산해 보자. 구면 위의 점 \(P(x,\,y,\,z)\)에서 이 구면에 수직이고 바깥쪽을 향하는 법선벡터는 \(\overrightarrow{OP}\)와 평행하므로 \[\mathbf{n} = \frac{\overrightarrow{OP}}{\lvert\,\overrightarrow{OP}\,\rvert} = \frac{x\,\mathbf{i} + y\,\mathbf{j} + z\,\mathbf{k}}{a}\] 이다. 그러므로 \[\mathbf{F} \cdot \mathbf{n} \,d\sigma = \frac{x^2 + y^2 + z^2}{a} d\sigma = \frac{a^2}{a} d\sigma= a\,d\sigma \] 이며 \[\iint_S \mathbf{F} \cdot \mathbf{n} \,d\sigma = \iint_S a\,d\sigma = a \cdot (\text{area of } S) = 4\pi a^3\tag{4.4}\] 이다.
다음으로 \(D\)에서의 유출밀도의 적분, 즉 (4.3)의 우변을 계산해 보자. \[\nabla \cdot \mathbf{F} = \frac{\partial}{\partial x}x + \frac{\partial}{\partial y}y + \frac{\partial}{\partial z}z = 3\] 이므로 \[\iiint_D \nabla \cdot \mathbf{F} \,dV = \iiint_D 3 \,dV = 3\cdot (\text{volume of }D) = 4\pi a^3\tag{4.5} \] 이다. 계산 결과 (4.4)와 (4.5)를 비교하면 일치한다.
발산 정리의 응용
(3.1)과 비슷한 등식이 발산과 회전에 대하여 성립한다. 즉 벡터장 \(\mathbf{F} = M\,\mathbf{i} + N\,\mathbf{j} + P\,\mathbf{k}\)가 연속인 2계 편도함수를 가지면 다음이 성립한다.
등식 (5.1)을 증명해 보자. 발산과 회전의 정의를 따라 계산하면 다음을 얻는다. \[\begin{align} \opdiv (\curl \,\mathbf{F} ) &= \nabla \cdot (\nabla \times \mathbf{F} )\\[5pt] &= \frac{\partial}{\partial x}\left( \frac{\partial P}{\partial y} - \frac{\partial N}{\partial z}\right) + \frac{\partial}{\partial y}\left( \frac{\partial M}{\partial z} - \frac{\partial P}{\partial x}\right) + \frac{\partial}{\partial z}\left( \frac{\partial N}{\partial x} - \frac{\partial M}{\partial y}\right) \\[5pt] &= \frac{\partial^2 P}{\partial x\,\partial y} - \frac{\partial^2 N}{\partial x\,\partial z} + \frac{\partial^2 M}{\partial y\,\partial z} - \frac{\partial^2 P}{\partial y \,\partial x} + \frac{\partial^2 N}{\partial z\,\partial x} - \frac{\partial^2 M}{\partial z\,\partial y}\\[5pt] &= \left(\frac{\partial^2 P}{\partial x\,\partial y} - \frac{\partial^2 P}{\partial y \,\partial x}\right) + \left(\frac{\partial^2 M}{\partial y\,\partial z} - \frac{\partial ^2 M}{\partial z\,\partial y}\right) + \left(\frac{\partial^2 N}{\partial z\,\partial x} - \frac{\partial^2 N}{\partial x\,\partial z}\right) .\tag{5.2} \end{align}\] 클래로의 정리에 의하여, (5.2)의 마지막 식에서 괄호로 묶인 각 식의 값은 \(0\)이다. 그러므로 (5.2)의 결과는 \(0\)이다. 즉 등식 (5.1)을 얻는다.
등식 (5.1)의 결과로서 다음을 얻는다.
정리 3. \(\opdiv \,\mathbf{G} \ne 0\)이면 \(\mathbf{G} = \curl\,\mathbf{F}\)인 벡터장 \(\mathbf{F}\)는 존재하지 않는다.
발산 정리의 또 다른 예로서 전자기 이론의 가우스 법칙(Gauss' law)을 살펴보자.
정리 4. (전자기 이론의 가우스 법칙) 3차원 공간에서 점전하 \(q\)를 안쪽에 품는 닫힌 단순곡면 \(S\)가 있을 때, \(q\)에 의하여 생기는 전기장이 \(S\)에 작용하는(\(S\)를 가로질러 바깥으로 나가는) 총 전기력은 \[\frac{q}{\epsilon_0}\] 이다. (\(q\)와 \(\epsilon_0\)에 대한 설명은 이 법칙을 유도하는 과정에서 설명한다.)
가우스 법칙을 유도하는 과정은 3단계로 나눌 수 있다.
1단계. \(a\)와 \(b\)가 \(a > b\)인 양수라고 하자. 이때 영역 \[D : \,\, b^2 \le x^2 + y^2 + z^2 \le a^2\] 의 경계를 통과하는 벡터장 \[\mathbf{F} = \frac{x\,\mathbf{i} + y\,\mathbf{j} + z\,\mathbf{k}}{\rho^2} ,\,\, \rho=\sqrt{x^2 + y^2 + z^2}\tag{5.3}\] 의 외향유출을 구하자.
먼저 \[\frac{\partial \rho}{\partial x} = \frac{1}{2} (x^2 +y^2 +z^2 )^{-1/2} \cdot 2x = \frac{x}{\rho}\] 이므로 \[\frac{\partial M}{\partial x} = \frac{\partial}{\partial x}(x\rho^{-3}) = \rho^{-3} - 3x\rho^{-4} \frac{\partial\rho}{\partial x} = \frac{1}{\rho^3} - \frac{3x^2}{\rho^5}\] 이다. 같은 방법으로 \(N_y\)와 \(P_z\)를 구하면 \[\frac{\partial N}{\partial y} = \frac{1}{\rho^3} - \frac{3y^2}{\rho^5} ,\,\, \frac{\partial P}{\partial z} = \frac{1}{\rho^3} - \frac{3z^2}{\rho^5}\] 이다. 이로써 \(\mathbf{F}\)의 발산이 \[\opdiv \,\mathbf{F} = \frac{3}{\rho^3} - \frac{3}{\rho^5} (x^2 + y^2 + z^2 ) = \frac{3}{\rho^3} - \frac{3\rho^2}{\rho^5} = 0 \tag{5.4}\] 이므로, \(D\)이 경계를 통과하는 \(\mathbf{F}\)의 외향 유출은 \(0\)이다.
2단계. 중심이 원점이고 반지름이 \(a\)인 구면 \(S_a\)를 통과하는 \(\mathbf{F}\)의 외향유출을 구하자. 보기 4에서 살펴본 바와 같이 구면 \(S_a\) 표면에서 바깥쪽을 향하는 단위법선벡터는 \[\mathbf{n} = \frac{x\,\mathbf{i} + y\,\mathbf{j} + z\,\mathbf{k}}{\sqrt{x^2 + y^2 + z^2}} = \frac{x\,\mathbf{i} + y\,\mathbf{j} + z\,\mathbf{k}}{a}\] 이다. 그러므로 \[\begin{align} \mathbf{F} \cdot \mathbf{n} &= \frac{x\,\mathbf{i} + y\,\mathbf{j} + z\,\mathbf{k}}{a^3} \cdot \frac{x\,\mathbf{i} + y\,\mathbf{j} + z\,\mathbf{k}}{a} \\[5pt] &= \frac{x^2 + y^2 + z^2}{a^4} = \frac{a^2}{a^4} = \frac{1}{a^2},\\[5pt] \iint_{S_a} \mathbf{F} \cdot \mathbf{n} \,d\sigma &= \frac{1}{a^2} \iint_{S_a} d\sigma = \frac{1}{a^2} \cdot 4\pi a^2 = 4 \pi\tag{5.5} \end{align}\] 이다.
3단계. 3차원 좌표공간에서 원점에 놓인 점전하 \(q\)로부터 생기는 전기장은 다음과 같다. \[\begin{align} \mathbf{E} (x,\,y,\,z) &= \frac{1}{4\pi \epsilon_0} \frac{q}{\lvert\mathbf{r}\rvert^2} \left( \frac{\mathbf{r}}{\lvert\mathbf{r}\rvert}\right) \\[7pt] &= \frac{q}{4\pi\epsilon_0} \frac{\mathbf{r}}{\lvert\mathbf{r}\rvert^3} \\[7pt] &= \frac{q}{4\pi\epsilon_0}\frac{x\,\mathbf{i} + y \,\mathbf{j} + z\,\mathbf{k}}{\rho^3} . \end{align}\] 여기서 \(\epsilon_0\)는 물리적 상수이고 \(\mathbf{r}\)는 점 \((x,\,y,\,z)\)의 위치벡터이며 \(\rho = \lvert\mathbf{r}\rvert\)이다. (5.3)을 이용하면 \[\mathbf{E} = \frac{q}{4\pi\epsilon_0}\mathbf{F}\] 로 나타낼 수 있다.
\(S\)가 원점을 안쪽에 품는 닫힌 단순곡면이고 \(S_a\)가 \(S\)를 안쪽에 품는 구면이라고 하자(그림 7).
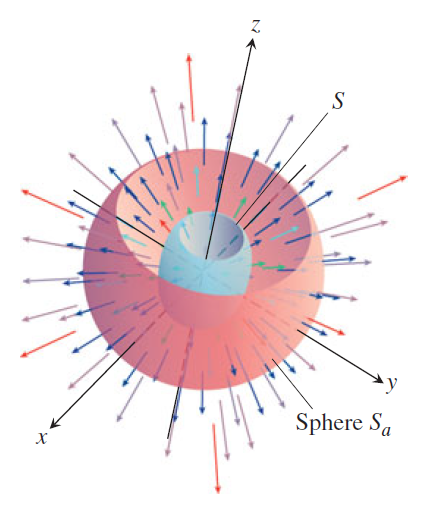
(5.4)에 의하여 \[\nabla\cdot\mathbf{E} = \nabla \cdot \frac{q}{4\pi\epsilon_0}\mathbf{F} = \frac{q}{4\pi\epsilon_0} \nabla \cdot \mathbf{F} = 0\] 이므로 \(S\)와 \(S_a\) 사이의 영역 \(D\)에서 \(\nabla \cdot \mathbf{E}\)의 삼중적분은 \(0\)이다. 그러므로 발산 정리에 의하여 \[\iint_{\partial D} \mathbf{E} \cdot \mathbf{n} \,d\sigma = \iiint_{D} \nabla \cdot \mathbf{E} \,dV = 0\tag{5.6}\] 이다. 여기서 \(\partial D\)는 \(D\)의 경계, 즉 두 개의 곡면 \(S\)와 \(S_a\)의 합집합으로 이루어진 곡면을 나타낸다. 곡면 \(S\)의 바깥쪽 방향은 영역 \(D\)의 안쪽을 향하는 방향이며, 곡면 \(S_a\)의 바깥쪽 방향은 영역 \(D\)의 바깥을 향하는 방향이다. 그러므로 \[\iint_{\partial D} \mathbf{E} \cdot \mathbf{n} \,d\sigma = - \iint_{S} \mathbf{E} \cdot \mathbf{n} \,d\sigma + \iint_{S_a} \mathbf{E} \cdot \mathbf{n} \,d\sigma\tag{5.7}\] 이다. 이 등식의 좌변은 (5.6)에 의하여 \(0\)이고, 우변의 두 번째 적분의 값은 (5.5)의 값에 \(q / (4\pi\epsilon_0)\)를 곱한 것과 같다. 그러므로 \[\iint_{S} \mathbf{E} \cdot \mathbf{n} \,d\sigma = \iint_{S_a} \mathbf{E} \cdot \mathbf{n} \,d\sigma = \frac{q}{\epsilon_0}\tag{5.8}\] 이다. 이 값은 점전하 \(q\)가 위치한 지점(원점)을 안쪽에 품는 임의의 닫힌 단순곡면 \(S\)에 대하여 성립한다.
