좌극한과 우극한

$x$ 축에서 한 점 $c$ 에 다가갈 수 있는 방향은 두 가지가 있다. 즉 $c$ 의 왼쪽에서 $c$ 에 다가갈 수도 있으며, $c$ 의 오른쪽에서 $c$ 에 다가갈 수도 있다. 이와 같이 $x$ 가 $c$ 에 다가가는 방향에 따라 $c$ 에서 $f$ 의 극한을 구분할 수 있다.

좌극한과 우극한의 정의

$x$ 가 $c$ 의 왼쪽에서 $c$ 에 접근할 때 $f (x)$ 의 값이 $L$ 에 다가가면 $f$ 는 $c$ 에서 좌극한 $L$ 을 가진다고 말한다. 우극한에 대해서도 비슷한 방법으로 정의한다. 논리적인 정의는 다음과 같다.

정의 1. (좌극한과 우극한)

$L$ 과 $c$ 가 실수이고 함수 $f : D \to R$ 가 $c$ 를 오른쪽 끝점으로 하는 한 열린 구간에서 정의되었다고 하자. 만약 임의의 $ϵ > 0$ 에 대하여 $δ > 0$ 이 존재하여 $0 < c - x < δ$ 인 모든 $x \in D$ 에 대하여 $| f (x) - L | < ϵ$ 이 성립하면 ‘ $f$ 는 $c$ 에서 좌극한 $L$ 을 가진다’라고 말하고, $f (x) \to L as x \to c^{-}$ 또는 $lim_{x \to c^{-}} f (x) = L$ 또는 $f (c^{-}) = L$ 로 나타낸다.
$L$ 과 $c$ 가 실수이고 함수 $f : D \to R$ 가 $c$ 를 왼쪽 끝점으로 하는 한 열린 구간에서 정의되었다고 하자. 만약 임의의 $ϵ > 0$ 에 대하여 $δ > 0$ 이 존재하여 $0 < x - c < δ$ 인 모든 $x \in D$ 에 대하여 $| f (x) - L | < ϵ$ 이 성립하면 ‘ $f$ 는 $c$ 에서 우극한 $L$ 을 가진다’라고 말하고, $f (x) \to L as x \to c^{+}$ 또는 $lim_{x \to c^{+}} f (x) = L$ 또는 $f (c^{+}) = L$ 로 나타낸다.

극한값이 존재하지 않는 곳에서도 좌극한이나 우극한은 존재할 수 있다.

보기 1. 함수 $f$ 가 다음과 같이 주어졌다고 하자. $f (x) = {\begin{cases} 7 & if x > 1 \\ 0 & if x \leq 1 \end{cases}$ 이 때 $1$ 에서 $f$ 의 극한값은 존재하지 않지만 $lim_{x \to 1^{-}} f (x) = 0, lim_{x \to 1^{+}} f (x) = 7$ 로서 $1$ 에서 $f$ 의 좌극한과 우극한은 각각 존재한다.

함수가 구간에서 정의되어 있을 때 구간의 왼쪽 끝점에서는 우극한과 극한을 동일시하며, 구간의 오른쪽 끝점에서는 좌극한과 극한을 동일시한다.

보기 2. 함수 $f$ 가 반열린 구간 $(3, 5]$ 에서 $f (x) = x^{2}$ 으로 정의되어 있다고 하자. 이 때 $lim_{x \to 3} f (x) = lim_{x \to 3^{+}} f (x) = 9,$ $lim_{x \to 5} f (x) = lim_{x \to 5^{-}} f (x) = 25$ 이다. 또한 $3 < c < 5$ 인 점 $c$ 에 대해서는 $lim_{x \to c} f (x) = lim_{x \to c^{-}} f (x) = lim_{x \to c^{+}} f (x) = c^{2}$ 이다.

한방향 극한과 양방향 극한의 관계

좌극한과 우극한을 통틀어 한방향 극한이라고 부른다. 한방향 극한과 구분하기 위하여 일반적인 극한을 양방향 극한이라고 부른다.

보기 2에서 본 것처럼 함수의 정의역이 구간일 때, 구간의 왼쪽 끝점에서는 극한과 우극한이 동일한 개념이며, 구간의 오른쪽 끝점에서는 극한과 좌극한이 동일한 개념이다.

그러므로 양방향 극한이라는 용어는 $f$ 가 $c$ 를 원소로 갖는 한 열린구간의 $c$ 를 제외한 모든 점에서 정의되었을 때, 즉 $x$ 가 $c$ 의 왼쪽으로부터 $c$ 에 다가갈 수 있고, $c$ 의 오른쪽으로부터도 $c$ 로 다가갈 수 있는 상황에서만 사용하기로 한다.

정리 1. $c$ 와 $L$ 이 실수이고 함수 $f$ 가 $c$ 를 원소로 갖는 한 열린구간의 $c$ 를 제외한 모든 점에서 정의되었다고 하자. 이 때 $lim_{x \to c} f (x) = L$ 일 필요충분조건은 $lim_{x \to c^{-}} f (x) = L and lim_{x \to c^{+}} f (x) = L$ 인 것이다.

증명

먼저 필요조건을 증명하자. $c$ 에서 $f$ 의 극한값이 $L$ 이라고 가정하자. 그리고 $ϵ > 0$ 이 임의로 주어졌다고 하자. 극한의 정의에 의하여 $δ > 0$ 이 존재하여 $0 < | x - c | < δ$ 인 임의의 $x$ 에 대하여 $\begin{matrix} (1) & | f (x) - L | < ϵ \end{matrix}$ 이 성립한다. 그런데 $\begin{matrix} (2) & 0 < c - x < δ \end{matrix}$ 또는 $\begin{matrix} (3) & 0 < x - c < δ \end{matrix}$ 어느 때나 $0 < | x - c | < δ$ 가 성립하므로 (1)이 성립한다. 그러므로 (2), (1)에 의하여 $lim_{x \to c^{-}} f (x) = L$ 이며, (3), (1)에 의하여 $lim_{x \to c^{+}} f (x) = L$ 이다.

다음으로 충분조건을 증명하자. $c$ 에서 $f$ 의 좌극한과 우극한이 모두 $L$ 이라고 가정하자. 그리고 $ϵ > 0$ 이 임의로 주어졌다고 하자. 좌극한의 정의에 의하여 $δ_{1} > 0$ 이 존재하여 $\begin{matrix} (4) & 0 < c - x < δ_{1} \end{matrix}$ 인 임의의 $x$ 에 대하여 $| f (x) - L | < ϵ$ 이 성립하며, 우극한의 정의에 의하여 $δ_{2} > 0$ 가 존재하여 $\begin{matrix} (5) & 0 < x - c < δ_{2} \end{matrix}$ 인 임의의 $x$ 에 대하여 $| f (x) - L | < ϵ$ 이 성립한다.

$δ = min {δ_{1}, δ_{2}}$ 라고 하자. 그러면 $0 < | x - c | < δ$ 인 $x$ 는 (4) 또는 (5) 중 하나를 반드시 만족시키므로, 그러한 $x$ 에 대하여 $| f (x) - L | < ϵ$ 이 성립한다.

한방향 극한의 예: $(\sin x) / x$ 의 극한

삼각함수의 성질을 증명할 때 자주 사용되는 극한 공식을 하나 살펴보자.

정리 2. ( $(\sin θ) / θ$ 의 극한) $\begin{matrix} (6) & lim_{θ \to 0} \frac{\sin θ}{θ} = 1 (θ in radians) \end{matrix}$

증명

$θ = 0$ 에서 $(\sin θ) / θ$ 의 좌극한과 우극한의 값이 모두 $1$ 임을 보이자. 먼저 $0 < θ < π / 2$ 인 경우를 살펴보자.

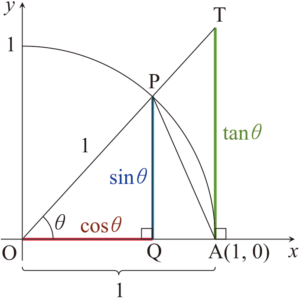
그림와 같이 좌표펴면의 제 1 사분면에 반지름이 $1$ 이고 원점이 중심인 사분원을 그린다. 그리고 $∠ POA = θ$ 가 되도록 사분원 위의 점 $P$ 를 잡는다. 점 $P$ 에서 $x$ 축에 내린 수선의 발을 $Q$ 라고 하고, 점 $A (1, 0)$ 을 지나고 $x$ 축과 수직인 직선이 반직선 $OP$ 와 만나는 점을 $T$ 라고 하자. 그러면 $\sin θ = \overset{―}{PQ}, \cos θ = \overset{―}{OQ}, \tan θ = \overset{―}{TA}$ 이다. 그런데 $(Area △ OAP) \leq (Area sector OAP) \leq (Area △ OAT)$ 이므로 $\frac{1}{2} \sin θ \leq \frac{1}{2} θ \leq \frac{1}{2} \tan θ$ 이다. $0 < θ < π / 2$ 의 범위에서 위 부등식의 각 항은 모두 양수이므로, 각 항에 $2$ 를 곱하고 각 항을 $\sin θ$ 로 나누면 $1 < \frac{θ}{\sin θ} < \frac{1}{\cos θ}$ 이며, 세 항의 역수를 취하면 $1 > \frac{\sin θ}{θ} > \cos θ$ 를 얻는다. 그런데 $θ \to 0^{+}$ 일 때 $\cos θ \to 1$ 이므로, 위 부등식과 샌드위치 정리에 의하여 $lim_{θ \to 0^{+}} \frac{\sin θ}{θ} = 1$ 을 얻는다. 한편 $(\sin θ) / θ$ 는 우함수이므로 $0$ 에서 이 함수의 좌극한과 우극한은 일치한다. 그러므로 $lim_{θ \to 0} \frac{\sin θ}{θ} = 1$ 을 얻는다.

보기 3. 다음 극한값을 구해 보자. $lim_{h \to 0} \frac{\cos h - 1}{h}$ $\cos h = 1 - 2 \sin^{2} (h / 2)$ 이므로 정리 2에 의하여 $\begin{aligned} lim_{h \to 0} \frac{\cos h - 1}{h} & = lim_{h \to 0} \frac{- \sin^{2} (h / 2)}{h / 2} \\ \leftarrow θ = h / 2 & = - lim_{θ \to 0} \frac{\sin θ}{θ} \sin θ \\ = - 1 \times 0 = 0. \end{aligned}$

보기 4. $a \neq 0,$ $b \neq 0$ 일 때 다음 극한값을 구해 보자. $lim_{x \to 0} \frac{\sin a x}{b x}$ 정리 2에 의하여 $\begin{aligned} lim_{x \to 0} \frac{\sin a x}{b x} & = lim_{x \to 0} \frac{\sin a x}{a x} \cdot \frac{a}{b} \\ = \frac{a}{b} \cdot lim_{h \to 0} \frac{\sin h}{h} \\ = \frac{a}{b} \cdot 1 = \frac{a}{b} . \end{aligned}$

좌극한과 우극한