지수함수와 로그함수

\(a\)가 복소수이고 \(n\)이 양의 정수일 때, 지수가 자연수인 거듭제곱을 다음과 같이 정의한다. \[a^1 = a ,\quad a^{n+1} = a^n \cdot a .\] 만약 \(a\)가 음이 아닌 복소수라면, 지수가 \(0\)인 거듭제곱과 지수가 음의 정수인 거듭제곱을 다음과 같이 정의한다. \[a^0 = 1 ,\quad a^{-n} = \frac{1}{a^n}.\] 만약 \(a\)가 양의 실수라면 \(b^n = a\)를 만족시키는 양수 \(b\)가 유일하게 존재한다. 그러므로 \[a^{\frac{1}{n}}=b \quad \Longleftrightarrow \quad \left( a=b^n \,\,\text{and}\,\, b > 0 \right) \] 으로 정의한다. 만약 \(a\)가 양의 실수이고 \(m\)과 \(n\)이 양의 정수라면, 지수가 유리수인 거듭제곱을 다음과 같이 정의한다. \[a^{\frac{m}{n}} = \left( a^{\frac{1}{n}}\right)^m \quad\text{and}\quad a^{-\frac{m}{n}} = \frac{1}{a^{\frac{m}{n}}} .\] 만약 \(a\)가 \(1\)보다 큰 실수이고 \(r\)가 실수라면, 지수가 실수인 거듭제곱을 다음과 같이 정의한다. \[a^r = \left( \text{the least upper bound of the set } \left\{ a^q \,\vert\, q < r \,\,\text{and}\,\, q\in\mathbb{Q} \right\} \right) .\] 만약 \(0 < a < 1\)이고 \(r\)가 실수라면 \[a^r = \frac{1}{\left( \frac{1}{a} \right)^r}\] 로 정의한다. 만약 \(a=1\)이면 당연히 \(a^r = 1\)로 정의한다.

\(a\)가 양수이면 임의의 실수 \(x\)에 대하여 거듭제곱 \(a^x\)이 정의된다. 그러므로 \[f : \mathbb{R} \rightarrow \mathbb{R} ,\,\, f(x) = a^x\] 은 잘 정의된 함수이다. 이와 같은 함수 \(f\)를 밑이 \(\boldsymbol{a}\)인 지수함수(exponential function of base \(a\))라고 부른다. 이 함수는 \(a < 1\)이면 감소하는 함수이고, \(a > 1\)이면 증가하는 함수이다.

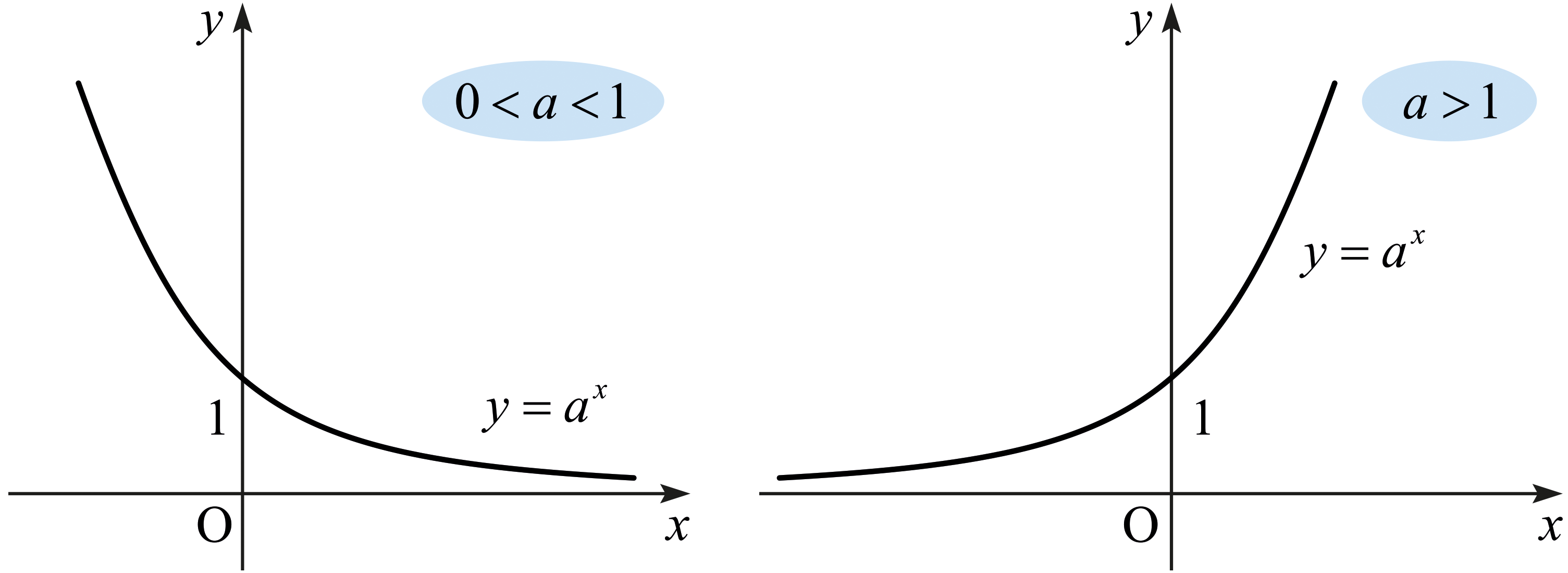
만약 \(a = 1\)이면 \(f(x)=a^x\)으로 정의된 함수 \(f\)는 상수함수이다. 그러므로 “\(f(x)=a^x\)이 지수함수이다”라고 말할 땐 \(a > 0\)과 \(a\ne 1\)을 가정한 것이라 약속한다.

\(a > 0\)이고 \(a\ne 1\)이면, 함수 \(x \mapsto a^x\)은 \(\mathbb{R}\)로부터 \(\mathbb{R}^+\)로의 일대일 대응이다. 그러므로 이 함수의 역함수가 존재하며, 그 역함수는 \(\mathbb{R}^+\)로부터 \(\mathbb{R}\)로의 함수이다.

\(a > 0\)이고 \(a\ne 1\)일 때, \(\log _a x\)를 \(x > 0\)에 대하여 다음과 같이 정의한다. \[y = \log _a x \quad \Longleftrightarrow \quad a^y = x .\] 이때 양수 \(x\)를 \(\log_a x\)에 대응시키는 함수를 밑이 \(\boldsymbol{a}\)인 로그함수(logarithmic function of base \(a\))라고 부른다. 이 함수는 \(a < 1\)이면 감소하는 함수이고, \(a > 1\)이면 증가하는 함수이다.

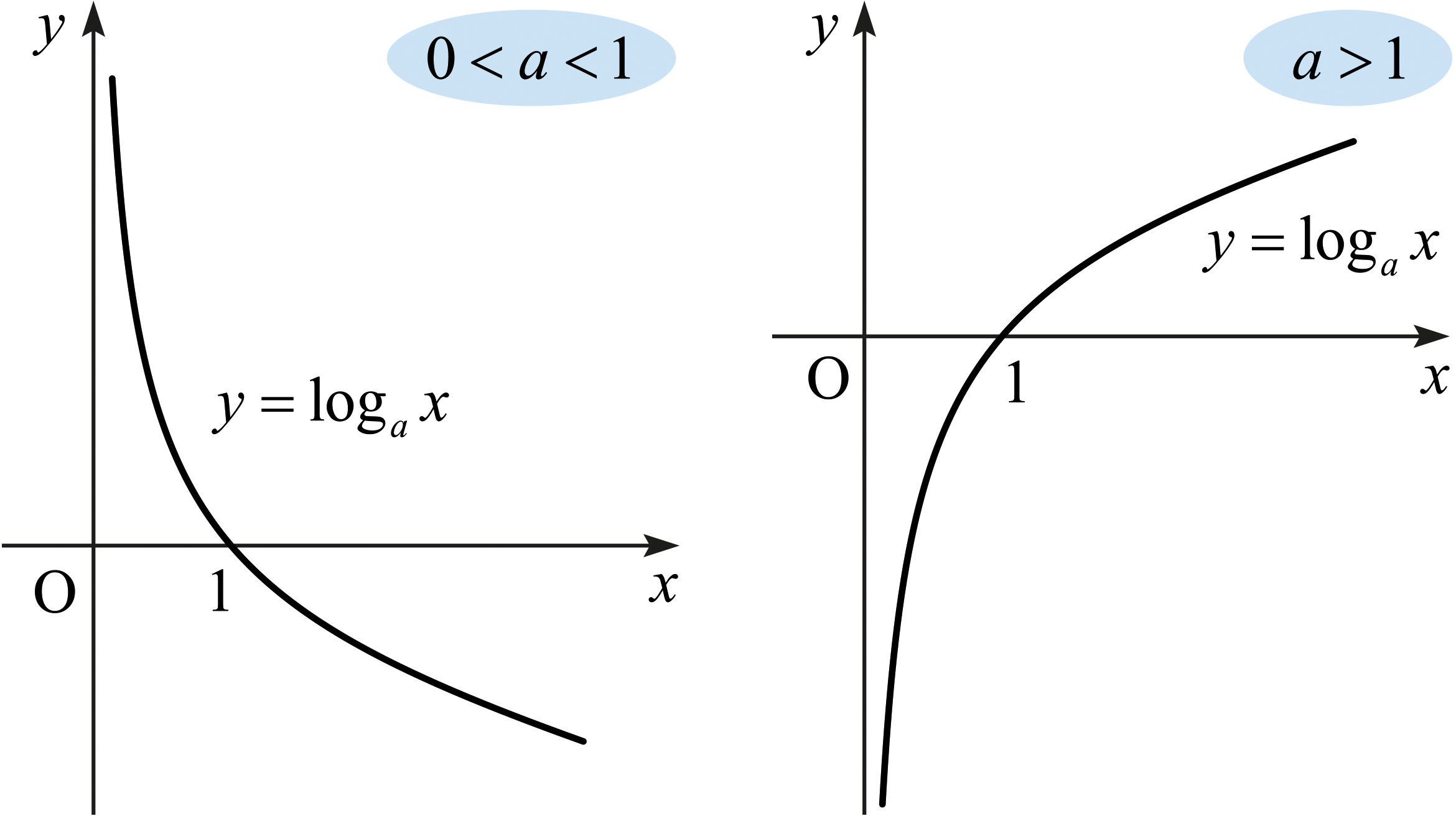
\(a > 0\)이고 \(a\ne 1\)일 때, 지수함수 \(y = a^x\)와 로그함수 \(y = \log_a x\)는 모두 연속함수이다. 연속함수의 정의와 성질은 4장에서 살펴볼 것이다.

로그함수가 지수함수의 역함수이므로, 로그함수의 성질은 지수법칙으로부터 유도된다.