길이, 넓이, 부피

이 절에서는 적분을 이용하여 곡선의 길이, 회전면의 넓이, 입체도형의 부피 구하는 방법을 살펴보자.

곡선의 길이

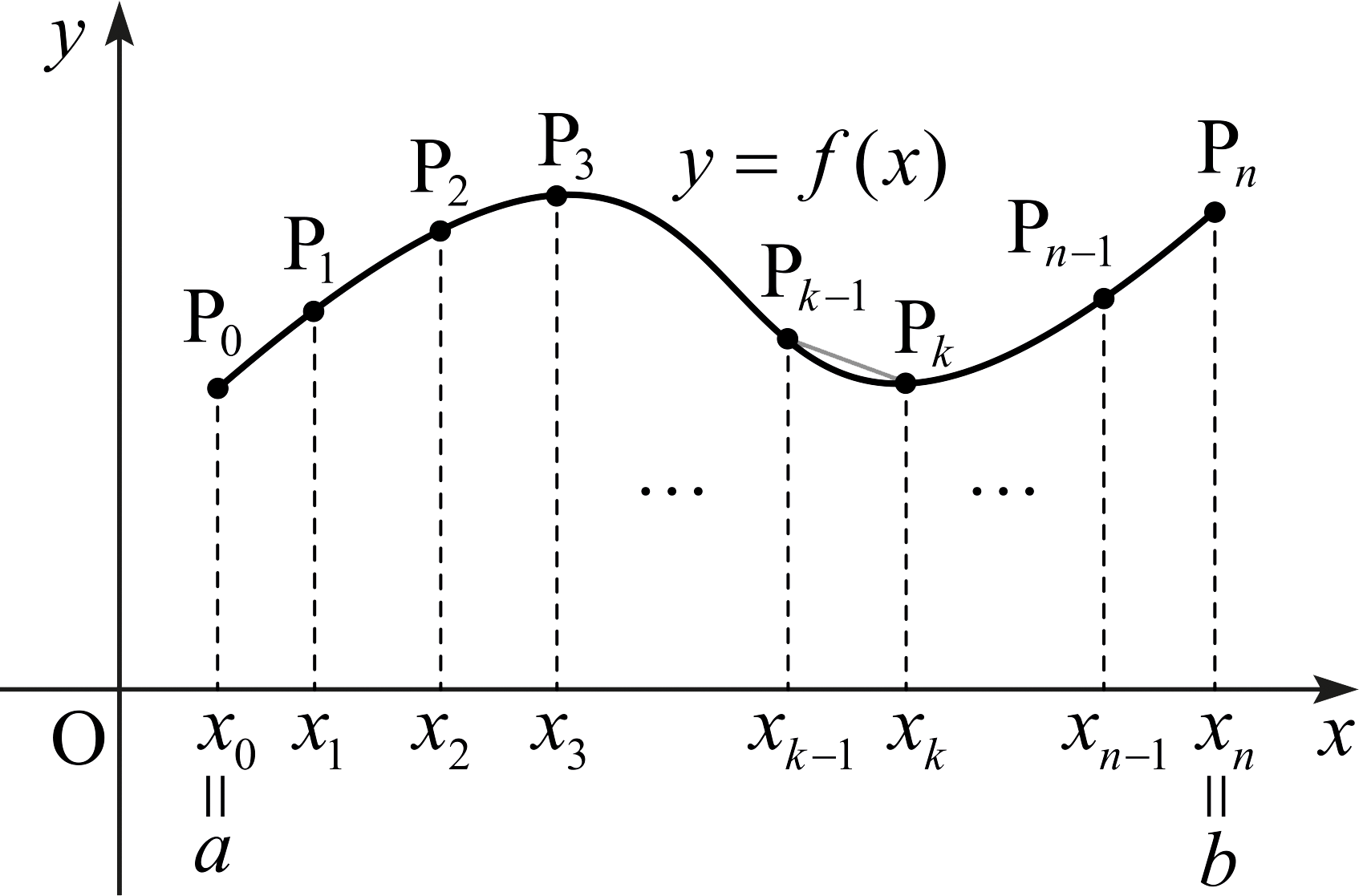
함수 \(f\)가 길이가 양수인 구간 \([a,\,b]\)에서 정의된 미분 가능한 실숫값 함수라고 하자. 이제 \(a\le x le b\)의 범위에서 \(y=f(x)\)의 그래프의 길이를 구해 보자.

구간 \([a,\,b]\)를 \(n\)개의 소구간 \(\left[ x_{i-1},\, x_i \right]\)로 분할하자. 즉 \[a = x_0 < x_1 < x_2 < \cdots < x_n = b\] 이다. \(k\)번째 소구간 \(\left[ x_{k-1},\, x_k \right]\)의 길이를 \(\Delta x_k\)라고 하자. 각 점 \(x_k\)는 곡선 위의 점 \(\mathrm{P}_k ( x_k ,\, f(x_k ))\)에 대응된다.

\(n\)의 값이 커질 수록 선분 \(\overline{\mathrm{P}_{k-1}\mathrm{P}_k}\)의 길이의 합 \[\overline{\mathrm{P}_0\mathrm{P}_1} + \overline{\mathrm{P}_1\mathrm{P}_2} + \cdots + \overline{\mathrm{P}_{n-1}\mathrm{P}_n} = \sum_{k=1}^{n} \overline{\mathrm{P}_{k-1}\mathrm{P}_k}\] 은 곡선의 길이에 가까워진다.

선분 한 조각의 길이는 \[\overline{\mathrm{P}_{k-1}\mathrm{P}_k} = \sqrt{ (x_k - x_{k-1})^2 + (f(x_k) - f(x_{k-1}))^2 }\] 이므로 평균값 정리에 의하여 \(x_k ^* \in ( x_{k-1} ,\, x_k )\)가 존재하여 \[f(x_k ) - f(x_{k-1}) = f ' (x_k ^* ) \Delta x_k\] 를 만족시킨다. 여기서 \(\Delta x_k - x_k - x_{k-1}\)이다. 따라서 \[\begin{align} \overline{\mathrm{P}_{k-1}\mathrm{P}_k} &= \sqrt{ (\Delta x_k )^2 + (\Delta x_k )^2 ( f ' (x_k ^* ))^2 } \\[5pt] &= \sqrt{ (1+ (f ' (x_k ^* ))^2 ) (\Delta x_k )^2} \\[5pt] &= \sqrt{1+ (f ' (x_k ^* ))^2} \Delta x_k \end{align}\] 이다. 그러므로 선분 조각들의 길이의 합은 \[\sum_{k=1}^n \overline{\mathrm{P}_{k-1}\mathrm{P}_k} =\sum_{k=1}^n \sqrt{ 1+(f ' (x_k ^* ))^2 }\Delta x_k\] 이다. 이 등식의 우변은 정적분의 부분합과 같다. 그러므로 \(x_k\)들로 이루어진 분할을 \(P\)라 할 때, \(\lVert P \rVert \rightarrow 0\)인 극한을 취하면 위 합은 \[\int_a^b \sqrt{ 1+ ( f ' (x))^2 } \,dx\] 에 수렴한다.

지금까지 다음 공식을 유도하였다.

회전면의 넓이

곡선이 곡선과 닿지 않은 직선을 축으로 회전하였을 때 생기는 곡면을 회전곡면(surface of revolution)이라고 부른다.

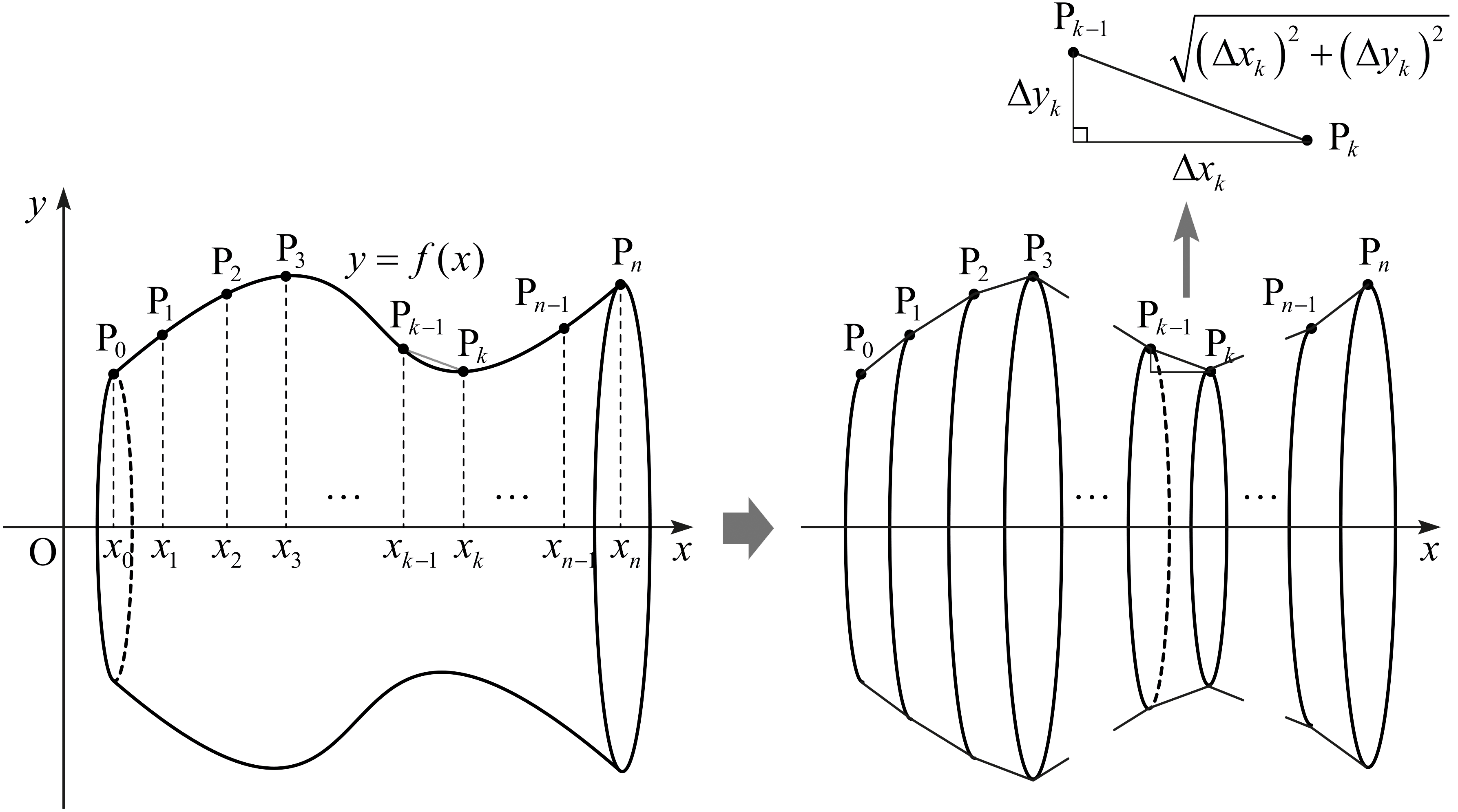
함수 \(f\)가 길이가 양수인 닫힌구간 \([a,\,b]\)에서 연속이고 구간 \((a,\,b)\)에서 미분 가능하며, \(a\le x \le b\)일 때 \(f(x) \ge 0\)이라고 하자. \(a\le x\le b\) 범위에서 곡선 \(y=f(x)\)를 \(x\)축에 대하여 한 바퀴 회전시켰을 때 자취가 만드는 곡면의 넓이 \(S\)를 구해 보자.

구간 \([a,\,b]\)가 \(n\)개의 소구간 \([x_{k-1} ,\, x_k ]\)들로 나누어지고, 각 소구간의 길이를 \(\Delta x_k\)라고 하자. 소구간의 양쪽 끝점에 대응되는 곡선 위의 점 \((x_{k-1} ,\, f(x_{k-1}))\)과 \((x_k ,\, f(x_k))\)를 이은 선분을 \(x\)축에 대하여 한 바퀴 회전시켰을 때 선분의 자취가 만드는 면(원뿔대의 옆면)의 넓이를 \(S_k\)라고 하자. 그러면 \(S_k\)의 합은 \(S\)의 근삿값이다.

\(S_k\)는 원뿔대의 옆면의 넓이이므로 다음과 같이 계산된다. \[2\pi \left( \frac{ f(x_{k-1}) + f(x_k) }{2} \right) \sqrt{ (\Delta x_k )^2 + (\Delta y_k )^2 } .\] 여기서 \[\frac{ f(x_{k-1}) + f(x_k) }{2}\] 는 \(f(x_{k-1})\)와 \(f(x_k)\) 사이의 값이므로 연속함수의 사잇값 정리에 의하여 \[\frac{ f(x_{k-1}) + f(x_k) }{2} = f(x_k ^* )\] 를 만족시키는 점 \(x_k^*\)가 열린구간 \((x_{k-1},\, x_k)\)에 존재한다. 또한 \[\sqrt{ (\Delta x_k )^2 + (\Delta y_k )^2 } = \sqrt{ 1+ \left( \frac{\Delta y_k}{\Delta x_k} \right)^2 } \Delta x_k\] 이다. 평균값 정리에 의하여 \[\frac{\Delta y_k}{\Delta x_k} = f ' (\xi _k )\] 를 만족시키는 점 \(\xi_k\)가 열린구간 \((x_{k-1} ,\, x_k )\)에 존재한다. 이로써 \(S_k\)들의 합은 \[\sum_{k=1}^{n} 2\pi f(x_k ^* )\sqrt{1+ ( ' (\xi _k ))^2} \Delta x_k\] 와 같이 표현된다. 점 \(x_k\)들로 이루어진 분할을 \(P\)라 하고 \(\lVert P \rVert \rightarrow 0\)인 극한을 취하면 \(x_k^*\)와 \(\xi_k\)의 거리는 \(0\)에 수렴하고, 이들은 모두 정적분의 변수 \(x\)가 된다. 그러므로 위 합은 다음 정적분에 수렴한다. \[2\pi \int_a^b f(x)\sqrt{1+(f ' (x))^2} \,dx\] 지금까지 다음 공식을 유도하였다.

평면에서 곡선이 매개변수 방정식으로 주어졌을 때에도 곡선의 길이를 구할 수 있다.

곡선이 매개변수 방정식 \(x=f(t),\) \(y=g(t)\)로 주어져 있다고 하자. \(t\)를 시각(time)이라고 생각하면 점 \((x,\,y)\)에서 속력은 \[v(t) = \sqrt{\left(\frac{dx}{dt}\right)^2 + \left(\frac{dy}{dt}\right)^2}\] 이다. 따라서 \(t_1 \le t \le t_2\)일 때 \(x=f(t),\) \(y=g(t)\)로 주어진 곡선의 길이는 \[\int_{t_1}^{t_2} \sqrt{ \left(\frac{dx}{dt}\right)^2 + \left(\frac{dy}{dt}\right)^2 } \,dt\] 이다. 이와 같은 곡선을 \(x\)축에 대하여 한 바퀴 회전시켰을 때 자취가 만드는 곡면의 넓이 \(S\)는 다음과 같다. \[S = 2\pi \int_{t_1}^{t_2} y\sqrt{ \left( \frac{dx}{dt}\right)^2 + \left(\frac{dy}{dt}\right)^2 } \,dt.\]

입체도형의 부피

평면에서 함수의 그래프로 둘러싸인 부분의 넓이를 구할 때 적분을 사용하는 것처럼 3차원 공간에서 그래프로 둘러싸인 부분의 부피를 구할 때도 적분을 사용할 수 있다.