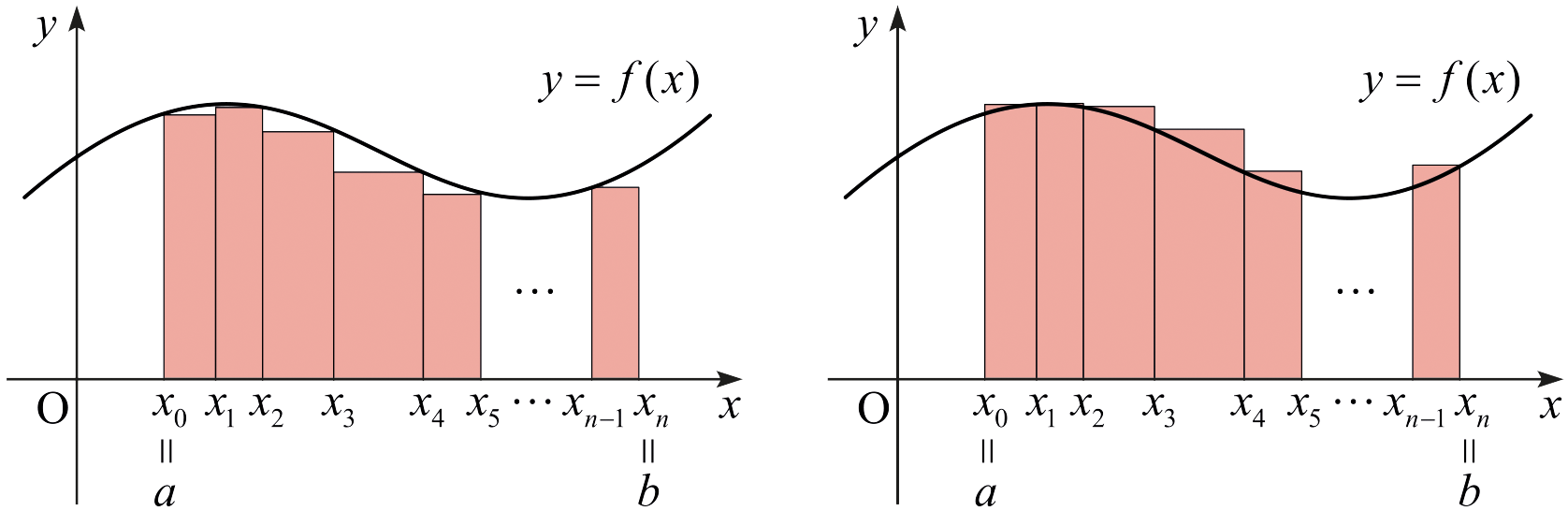이 글은 『미적분학 첫걸음』 6장 1절의 내용입니다. (미적분학 첫걸음 차례 보기)
정적분의 정의
\(a < b\)이고 \(f\)가 \(I=[a,\,b]\)에서 정의된 유계인 실숫값 함수라고 하자.
\(f\)가 \(I\)에서 연속이며 임의의 \(x\in I\)에 대하여 \(f(x) \ge 0\)이라고 가정하자. 그리고 곡선 \(y=f(x)\)와 \(x\)축, 두 직선 \(x=a,\) \(x=b\)로 둘러싸인 부분의 넓이를 \(A\)라고 하자. 구간 \(I\)에서 다음과 같은 \((n+1)\)개의 점 \(x_i\)를 택하자. \[a = x_0 < x_1 < x_2 < \cdots < x_{i-1} < x_i < \cdots < x_{n-1} < x_n = b.\] 이러한 점들의 모임을 \(P\)라고 하자. 즉 \[P = \left\{ x_0 ,\, x_1 ,\, x_2 ,\, \cdots ,\, x_n \right\}\] 이라고 하자. 이때 \(P\)를 \(I\)의 분할(partition)이라고 부른다. 이와 같이 주어진 분할 \(P\)의 점을 이용하여 \(I\)를 \(n\)개의 소구간으로 자를 수 있다: \[ \left[ x_0 ,\,x_1 \right] ,\,\, \left[ x_1 ,\,x_2 \right] ,\,\, \cdots ,\,\, \left[ x_{i-1} ,\,x_i \right] ,\,\, \cdots ,\,\, \left[ x_{n-1} ,\,x_n \right] .\] \(i\)번째 소구간의 길이를 \(\Delta x_i\)로 나타내자. 즉 \(\Delta x_i = x_i - x_{i-1}\)이라고 하자.
위 그림과 같이 소구간 \(\left[ x_{i-1} ,\, x_i \right]\)에서 \(f\)의 최솟값과 최댓값을 각각 \(m_i ,\) \(M_i\)로 나타내자. 그러면 다음 부등식을 얻는다. \[m_1 \Delta x_1 + m_2 \Delta x_2 + \cdots + m_n \Delta x_n \le A \le M_1 \Delta x_1 + M_2 \Delta x_2 + \cdots + M_n \Delta x_n . \tag{*}\] 위 부등식에서 가장 왼쪽의 합을 \(L(f,\,P)\)로, 가장 오른쪽의 합을 \(U(f,\,P)\)로 나타내자. 그러면 위 부등식은 다음과 같이 나타낼 수 있다. \[L(f,\,P) \le A \le U(f,\,P).\] 분할 \(P\)가 주어졌을 때 \(\Delta x_i\) 중 가장 큰 값을 \(P\)의 노름(norm)이라고 부르고 \(\lVert P \rVert\)로 나타낸다. 만약 \(\lVert P \rVert \rightarrow 0\)일 때 \(L(f,\,P)\)가 하나의 값 \(I_L\)에 한없이 가까워지면 \(I_L\)을 \(I\)에서 \(f\)의 하적분(lower integral)이라고 부르고 \[\underline \int_{a}^{b} f(x) dx\] 와 같이 나타낸다. 마찬가지로 만약 \(\lVert P \rVert \rightarrow 0\)일 때 \(U(f,\,P)\)가 하나의 값 \(I_U\)에 한없이 가까워지면 \(I_U\)를 \(I\)에서 \(f\)의 상적분(upper integral)이라고 부르고 \[\overline \int_{a}^{b} f(x) dx\] 와 같이 나타낸다.
만약 \([a,\,b]\)에서 \(f\)의 하적분과 상적분이 일치하면 “\(f\)는 \([a,\,b]\)에서 적분 가능하다”라고 말하고, \([a,\,b]\)에서 \(f\)의 하적분과 상적분을 ‘\([a,\,b]\)에서 \(f\)의 리만 적분(Riemann integral)’ 또는 간단히 ‘\([a,\,b]\)에서 \(f\)의 적분’이라고 부른다. \([a,\,b]\)에서 \(f\)의 적분을 다음과 같이 나타낸다. \[\int_a^b f(x) dx .\] 이와 같은 표현에서 \(x\)는 독립변수가 아니다. 예컨대 다음 식은 모두 같은 적분을 나타낸다. \[\int_a^b f(t) dt ,\quad \int_a^b f(s) ds ,\quad \int_a^b f(z)dz .\] 적분의 값은 \(a,\) \(b,\) \(f\)에 의하여 결정된다. 만약 \(a=b\)이면 \[\int_a^a f(x)dx =0\] 이라고 정의한다. 만약 \(a > b\)이면 \[\int_a^b f(x)dx =-\int _b^a f(x)dx\] 라고 정의한다.
지금까지 적분을 정의한 과정을 살짝 수정하면 \(f\)가 연속이 아닌 함수일 때도 적분을 정의할 수 있다. 만약 \(f\)가 소구간 \(\left[ x_{i-1} ,\,x_i \right]\)에서 연속이 아니라면 이 구간에서 \(f\)는 최댓값이나 최솟값을 갖지 않을 수도 있다. 하지만 만약 \(f\)가 이 구간에서 유계라면
“임의의 \(x\in \left[ x_{i-1} ,\, x_i \right]\)에 대하여 \(f(x) \le M_i\)”
를 만족시키는 \(M_i\) 중에서 가장 작은 값을 취하고,
“임의의 \(x\in \left[ x_{i-1} ,\, x_i \right]\)에 대하여 \(f(x) \ge m_i\)”
를 만족시키는 \(m_i\) 중에서 가장 큰 값을 취할 수 있다.
적분을 정의한 과정을 조심스럽게 살펴보면 \(f(x) \ge 0\)이라는 조건은 사용되지 않았다. 이 조건은 단지 ‘넓이’라는 직관적 개념을 바탕으로 시각적 심상을 형성하기 위해 필요했을 뿐이다. 그러므로 \(f(x) \ge 0\)이라는 조건 또한 적분을 정의하는 데에 필요하지 않다.
이로써 \(f\)가 구간 \([a,\,b]\)에서 유계일 때 \([a,\,b]\)에서 \(f\)의 적분이 정의되었다.
정적분의 기본 성질
이제 다음과 같은 두 가지 의문이 생긴다.
- 어떠한 함수가 적분 가능한다?
- 만약 적분 가능한 함수가 주어진다면 적분을 어떻게 계산하는가?
다음 정리는 첫 번째 질문에 대한 부분적인 답을 제시한다.
정리 6.1.1. (함수의 적분 가능성)
\(I\)가 길이가 양수인 닫힌구간이고 \(f\)가 \(I\)에서 정의된 유계인 실숫값 함수라고 하자.
- 만약 \(f\)가 \(I\)에서 연속이면 \(f\)는 \(I\)에서 적분 가능하다.
- 만약 \(f\)가 \(I\)에서 불연속인 점의 개수가 유한이면 \(f\)는 \(I\)에서 적분 가능하다.
증명
미적분학을 처음 공부한다면 이 정리의 증명을 생략해도 좋다. 그래도 보고 싶다면 [1]의 증명은 정적분의 정의 정리 5를 보기 바란다. [2]의 증명은 정적분의 정의 정리 7을 보기 바란다.
적분 가능성과 관련된 위와 같은 조건이 \(f\)가 적분 가능하기 위한 충분조건을 제공하기는 하지만 필요충분조건을 제공하지는 않는다. 하지만 미적분학 입문 수준에서는 위 정리만으로 적분의 성질을 논하는 데에 충분하다.
사실 함수 \(f\)가 구간 \([a,\,b]\)에서 리만 적분 가능할 필요충분조건은 \([a,\,b]\)에서 \(f\)가 불연속인 점의 측도가 \(0\)인 것이다. 이와 같은 정리를 르베그의 정리(Lebesgue's theorem)라고 부른다. 르베그의 정리를 깊이 공부하고 싶은 사람은 이 블로그의 글 적분 가능성에 대한 르베그의 정리를 보기 바란다.
보기 6.1.1.
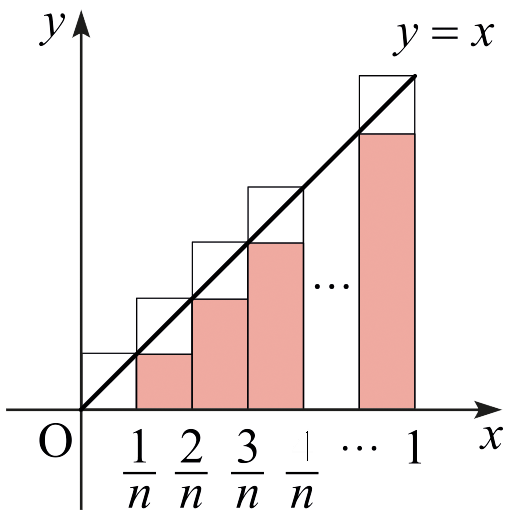
함수 \(f\)가 구간 \(I=[0,\,1]\)에서 \(f(x)=x\)로 주어졌다고 하자. \(f\)가 \(I\)에서 연속이므로 \(f\)는 \(I\)에서 적분 가능하다.
\(n\)이 (충분히 큰) 자연수라고 하고, 다음과 같은 점을 생각하자. \[x_i = \frac{i}{n} ,\quad (i=0,\,1,\,2,\,\cdots ,\,n ).\] 소구간 \(\left[ x_{i-1} ,\, x_i \right]\)에서 다음을 얻는다. \[\Delta x_i = \frac{1}{n} ,\quad m_i = f\left( x_{i-1} \right) = \frac{i-1}{n} ,\quad M_i = f\left( x_i \right) = \frac{i}{n}.\] \(I\)에서 \(f\)의 적분의 값을 \(A\)라고 하자. 그러면 다음 부등식을 얻는다. \[\left\{ \frac{0}{n} + \frac{1}{n} + \cdots + \frac{n-1}{n} \right\} \frac{1}{n} \le A \le \left\{ \frac{1}{n} + \frac{2}{n} + \frac{3}{n} + \cdots + \frac{n}{n} \right\} \frac{1}{n}.\] 이 상황을 그림으로 나타내면 다음과 같다.
부등식에서 합을 계산하면 \[\frac{n(n-1)}{2n^2} \le A \le \frac{n(n+1)}{2n^2}\] 이며, 식을 변형하면 \[\frac{1}{2} - \frac{1}{2n} \le A \le \frac{1}{2} + \frac{1}{2n}\] 을 얻는다. \(n\rightarrow\infty\)인 극한을 취하면 \(\Delta x_i \rightarrow 0\)이며, \[\frac{1}{2} \le A \le \frac{1}{2}\] 을 얻는다. 그러므로 \[\int_0^1 f(x) dx = \int_0^1 x \,dx = \frac{1}{2}\] 이다.
보기 6.1.2.
함수 \(f\)가 구간 \(I=[0,\,1]\)에서 \(f(x)=x^2\)으로 주어졌다고 하자. \(f\)가 \(I\)에서 연속이므로 \(f\)는 \(I\)에서 적분 가능하다.
\(n\)이 (충분히 큰) 자연수라고 하고, 다음과 같은 점을 생각하자. \[x_i = \frac{i}{n} ,\quad (i=0,\,1,\,2,\,\cdots ,\,n ).\] 소구간 \(\left[ x_{i-1} ,\, x_i \right]\)에서 다음을 얻는다. \[\Delta x_i = \frac{1}{n} ,\quad m_i = f\left( x_{i-1} \right) = \frac{(i-1)^2}{n^2} ,\quad M_i = f\left( x_i \right) = \frac{i^2}{n^2}.\] \(I\)에서 \(f\)의 적분의 값을 \(A\)라고 하자. 그러면 다음 부등식을 얻는다. \[\left\{ \frac{0^2}{n^2} + \frac{1^2}{n^2} + \cdots + \frac{(n-1)^2}{n^2} \right\} \frac{1}{n} \le A \le \left\{ \frac{1^2}{n^2} + \frac{2^2}{n^2} + \frac{3^2}{n^2} + \cdots + \frac{n^2}{n^2} \right\} \frac{1}{n}.\] 부등식에서 합을 계산하면 \[\frac{n(n-1)(2n-1)}{6n^3} \le A \le \frac{n(n+1)(2n+1)}{6n^3}\] 이다. \(n\rightarrow\infty\)인 극한을 취하면 \(\Delta x_i \rightarrow 0\)이며, \[\frac{2}{6} \le A \le \frac{2}{6}\] 을 얻는다. 그러므로 \[\int_0^1 x^2 \,dx = \frac{1}{3}\] 이다.
정적분은 다음과 같은 성질을 가진다.
정리 6.1.2. (정적분의 성질)
\(f\)와 \(g\)가 구간 \([a,\,b]\)에서 정의된 유계인 실숫값 함수라고 하자. \(f\)와 \(g\)가 모두 \([a,\,b]\)에서 적분 가능하다고 가정하고, \(k\)가 실수라고 하자. 그러면 \(f+g,\) \(f-g,\) \(kf\)가 모두 \([a,\,b]\)에서 적분 가능하며, 다음이 성립한다.
- \(\displaystyle \int_a^b \left\{ f(x) + g(x) \right\} dx = \int_a^b f(x) dx + \int_a^b g(x) dx. \)
- \(\displaystyle \int_a^b \left\{ f(x) - g(x) \right\} dx = \int_a^b f(x) dx - \int_a^b g(x) dx. \)
- \(\displaystyle \int_a^b k f(x) dx = k \int_a^b f(x) dx . \)
- 만약 임의의 \(x\in [a,\,b]\)에 대하여 \(f(x) \le g(x)\)이면 \[\displaystyle \int_a^b f(x) dx \le \int_a^b g(x) dx\]이다.
- 만약 \(a < c < b\)이면 \(f\)는 \([a,\,c]\)와 \([c,\,b]\)에서 적분 가능하며 \[\int_a^b f(x) dx = \int_a^c f(x) dx + \int_c^b f(x) dx \] 이다.
증명.
미적분학 입문 단계에서 이 정리의 증명은 생략한다. 직관적으로는 자명하지만 엄밀하게 증명하려면 꽤 까다롭다.
보기 6.1.3. 앞의 보기 6.1.1과 6.1.2의 결과를 이용하여 다음과 같이 다양한 함수의 적분을 계산할 수 있다.
- \(\displaystyle \int_0^1 (x^2 +x) dx = \int_0^1 x^2 dx + \int_0^1 x\,dx = \frac{1}{3} + \frac{1}{2} = \frac{5}{6}. \)
- \(\displaystyle \int_0^1 (x^2 -x) dx = \int_0^1 x^2 dx - \int_0^1 x\,dx = \frac{1}{3} - \frac{1}{2} = -\frac{1}{6}. \)
- \(\displaystyle \int_0^1 (3x^2 -5x)dx = 3\int_0^1 x^2 dx - 5\int_0^1 x\,dx = 3\times \frac{1}{3} - 5\times\frac{1}{2} = -\frac{3}{2}. \)
참고. 이 책에서는 함수 \(f\)가 구간 \([a,\,b]\)에서 유계인 경우에 한해서 \(f\)의 적분 가능성을 정의하였다. 이와 같은 정의에 따르면 \(f\)가 \([a,\,b]\)에서 유계가 아니라면 \([a,\,b]\)에서 \(f\)의 적분 가능성을 따지지 않는 것이 옳다.
하지만 정적분을 정의하는 다른 방법(리만 합의 극한)에서는 \(f\)가 \([a,\,b]\)에서 유계가 아닌 경우에도 \(f\)의 적분 가능성을 따진다. (그리고 그 결과는 “적분 가능하지 않다”이다.)
그러므로 우리는 \(f\)가 \([a,\,b]\)에서 유계가 아닌 경우 “\([a,\,b]\)에서 \(f\)의 적분 가능성을 따지지 않는다”라고 하지 않고 “\([a,\,b]\)에서 \(f\)가 적분 가능하지 않다”라고 하기로 약속하자.