이 글은 『미적분학 첫걸음』 5장 1절의 내용입니다. (미적분학 첫걸음 차례 보기)
함수 \(y=f(x)\)가 주어졌다고 하자. 여기서 \(x\)와 \(y\)는 실수 변수이다. 그리고 서로 다른 값 \(x_0,\) \(x_1\)을 생각하고 \[y_0 = f(x_0 ) ,\quad y_1 = f(x_1 )\] 이라고 하자. 만약 \(x\)가 \(x_0\)에서 \(x_1\)까지의 값을 취한다면 \(\boldsymbol x\)의 증가량은 \[\Delta x = x_1 - x_0\] 이고, \(\boldsymbol y\)의 증가량은 \[\Delta y = y_1 - y_0 = f(x_1 ) - f(x_0 ) = f(x_0 + \Delta x) - f(x_0 )\] 이다. 이때, \(x\)의 값이 \(x_0\)에서 시작하여 \(x_1\)에 이르는 동안 함수 \(f\)의 평균변화율(average rate of change)은 다음과 같다. \[\frac{\Delta y}{\Delta x} = \frac{f(x_1 ) - f(x_0 )}{x_1 - x_0} = \frac{f(x_0 + \Delta x ) -f(x_0 )}{\Delta x} .\]
보기 5.1.1. 함수 \(f(x) = x^2 -2x+5\)가 주어졌다고 하자. \(x\)의 값이 \(3\)에서 시작하여 \(3.2\)에 이르는 동안 \(f\)의 평균변화율을 구해 보자. \(x\)의 값의 증가량과 \(y\)의 값의 증가량은 각각 다음과 같다. \[\begin{align} \Delta x &= 0.2 , \\[6pt] \Delta y &= f(3.2) - f(3) = 8.84 - 8 = 0.84. \end{align}\] 그러므로 \(f\)의 평균변화율은 \[\frac{\Delta y}{\Delta x} = \frac{0.84}{0.2} = 4.2\] 이다.
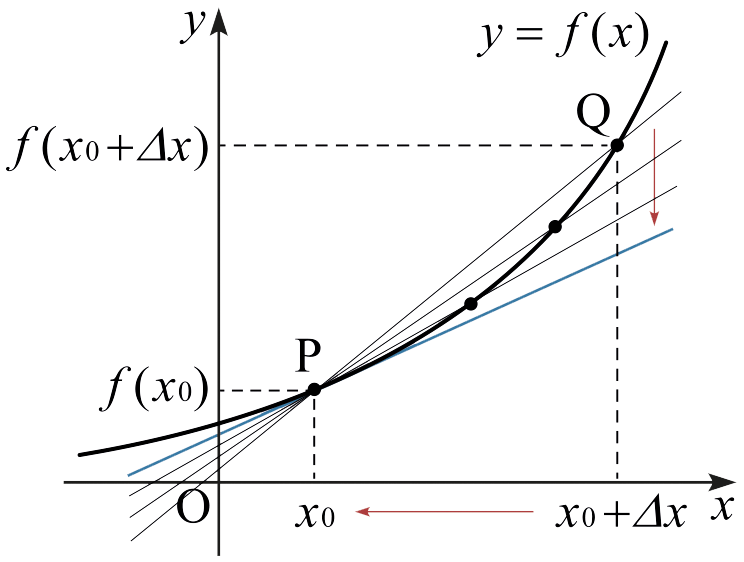
함수 \(y=f(x)\)의 그래프 위의 점 \((x_0 ,\, f(x_0 ))\)에서 이 그래프에 접하는 직선의 기울기를 구해 보자. 아래 그림을 살펴 보자.
함수의 그래프가 매끄럽다면 접선의 기울기는 다음 극한값과 같다. \[\lim_{\Delta x \rightarrow 0} \frac{f(x_0 + \Delta x) - f(x_0 )}{\Delta x}\] 만약 이 극한이 수렴한다면, 그 극한값을 \(x_0\)에서 \(f\)의 미분계수(derivative)라고 부르고 \(\boldsymbol{f ' (x_0 )}\)와 같이 나타낸다.
미분계수를 나타내는 기호는 다양하다. 다음 기호는 모두 \(x_0\)에서 \(f\)의 미분계수를 나타내는 기호이다. \[\begin{gather} f ' (x_0 ) \quad\quad \frac{d}{dx} f(x_0 ) \quad\quad \frac{df}{dx} (x_0 ) \quad\quad \left. \frac{df}{dx} \right\vert _{x=x_0} \\[7pt] \left. \frac{df}{dx} \right\vert _{x-x_0} \quad\quad Df(x_0 ) \quad\quad Df \bigg\vert _{x=x_0 } \end{gather}\]
예제 5.1.2. \(x_0 = 3\)에서 함수 \(f(x) = 2x^2 - 3x+5\)의 미분계수를 구하시오.
풀이. \(\Delta x \ne 0\)일 때 \[\begin{align} f(3+\Delta x ) - f(3) &= 2 (\Delta x)^2 + 9 \Delta x , \\[6pt] \frac{f(3+\Delta x) - f(3)}{\Delta x} &= \frac{2(\Delta x)^2 + 9 \Delta x}{\Delta x} = 2\Delta x+9 \end{align}\] 이다. 그러므로 \[\lim_{\Delta x \rightarrow 0} \frac{f(3+\Delta x) -f(3)}{\Delta x} = \lim_{\Delta x \rightarrow 0} (2\Delta x + 9 ) = 9\] 즉 \(f ' (3) = 9\)이다.
예제 5.1.3. \(x_0 = 3\)일 때 함수 \(y=2x^2 -3x+5\)의 그래프에 접하는 직선의 방정식을 구하시오.
풀이. \(x=3\)일 때 \(y=14\)이므로 접점의 좌표는 \((3,\,14)\)이다. \[\left. \frac{dy}{dx} \right\vert_{x=3} = 9\] 이므로 접선의 기울기는 \(9\)이다. 그러므로 접선의 방정식은 \[y = 9(x-3)+14\] 이다. 이 식을 간단하게 나타내면 \[y=9x-13\] 이다.
점 \(x_0\)에서 함수 \(f\)의 미분계수가 극한으로 정의되므로, \(x_0\)는 \(f\)의 정의역에 속하면서 동시에 \(f\)의 정의역의 집적점이어야 한다.
보기 5.1.4.
- 함수 \(f\)가 \(\mathbb{Z}\)에서 정의되었다면 \(\mathbb{Z}\)의 어느 점에서도 \(f\)의 미분계수가 정의되지 않는다. 왜냐하면 \(\mathbb{Z}\)는 집적점을 갖지 않기 때문이다.
- \((a,\,b)\)가 길이가 양수인 열린구간이고 \(f\)가 \((a,\,b)\)에서 정의되었다면 \((a,\,b)\)의 모든 점에서 \(f\)의 미분계수가 정의된다. (정의된다고 해서 반드시 존재하는 것은 아니다.) 열린구간의 끝점 \(a\)와 \(b\)에서는 \(f\)의 미분계수가 정의되지 않는다.
- \([a,\,b]\)가 길이가 양수인 닫힌구간이고 \(f\)가 \([a,\,b]\)에서 정의되었다면 \([a,\,b]\)의 모든 점에서 \(f\)의 미분계수가 정의된다.
만약 \(f\)가 길이가 양수인 닫힌구간 \([a,\,b]\)에서 정의되어 있다면, 다음 두 극한은 같은 극한을 나타낸다. \[\lim_{\Delta x \rightarrow 0} \frac{f(a+\Delta x ) - f(a)}{\Delta x} ,\quad \lim_{\Delta x \rightarrow 0^+} \frac{f(a+\Delta x ) - f(a)}{\Delta x}.\] 만약 두 번째 극한이 존재한다면, 이 극한을 \(a\)에서 \(f\)의 우미분계수(right-hand derivative)라고 부르고 \(f_r ' (a)\)와 같이 나타낸다. \(b\)에서 \(f\)의 좌미분계수도 같은 방법으로 정의된다. 즉 만약 극한 \[\lim_{\Delta x \rightarrow 0^-} \frac{f(b + \Delta x) -f(b)}{\Delta x}\] 가 존재한다면, 이 극한을 \(b\)에서 \(f\)의 좌미분계수(left-hand derivative)라고 부르고 \(f_l ' (b)\)와 같이 나타낸다.
만약 점 \(x_0\)에서 함수 \(f\)의 미분계수가 존재하면 “\(f\)가 \(x_0\)에서 미분 가능하다”라고 말한다.
만약 \(E\)가 함수 \(f:D \rightarrow \mathbb{R}\)의 정의역의 부분집합이고 \(f\)가 \(E\)의 모든 점에서 미분 가능하면 “\(f\)가 \(E\)에서 미분 가능하다”라고 말한다. 이 경우 \(f ' \)은 \(E\) 위에서 정의된 함수가 되는데, 이 함수 \(f ' \)을 \(f\)의 도함수(derivative, derived function)라고 부른다. 함수의 도함수를 구하는 것을 미분(differentiation)이라고 부른다. 즉 “도함수를 구한다”라는 말과 “미분한다”라는 말은 같은 뜻이다.
예제 5.1.5.
다음 함수를 \(x\)에 대하여 미분하시오.
(1) \(f(x) = 3x+1\)
(2) \(f(x) = x^2\)
(3) \(f(x) = \sqrt{x}\)
(4) \(f(t) = \sin t\)
풀이.
- 실수 \(x\)가 임의로 주어졌다고 하자. \[\begin{align} f ' (x) &= \lim_{\Delta x \rightarrow 0} \frac{f(x+\Delta x) - f(x)}{\Delta x} \\[4pt] &= \lim_{\Delta x \rightarrow 0} \frac{(3x + 3\Delta +1) - (3x+1)}{\Delta x} = 3. \end{align}\] 그러므로 \(f\)가 \(\mathbb{R}\)에서 미분 가능하며 \(f ' (x) = 3\)이다.
- 실수 \(x\)가 임의로 주어졌다고 하자. \[\begin{align} f ' (x) &= \lim_{\Delta x \rightarrow 0} \frac{f(x+ \Delta x) - f(x)}{\Delta x} \\[4pt] &= \lim_{\Delta x \rightarrow 0} \frac{(x+\Delta x)^2 - x^2}{\Delta x} \\[4pt] &= \lim_{\Delta x \rightarrow 0} (2x+\Delta x) = 2. \end{align}\] 그러므로 \(f\)가 \(\mathbb{R}\)에서 미분 가능하며 \(f ' (x) = 2x\)이다.
- 함수 \(f\)의 정의역은 \([0,\,\infty )\)이다. 만약 \(x > 0\)이면
\[\begin{align}
f ' (x) &= \lim_{\Delta x \rightarrow 0} \frac{f(x+\Delta x) - f(x)}{\Delta x} \\[4pt]
&= \lim_{\Delta x \rightarrow 0} \frac{\sqrt{x+\Delta x} - \sqrt{x}}{\Delta x} \\[4pt]
&= \lim_{\Delta x \rightarrow 0} \frac{(\sqrt{x+\Delta x} - \sqrt{x})(\sqrt{x+\Delta x} + \sqrt{x})}{\Delta x (\sqrt{x+\Delta x} + \sqrt{x})} \\[4pt]
&= \lim_{\Delta x \rightarrow 0} \frac{1}{\sqrt{x+\Delta x} + \sqrt{x}} = \frac{1}{2\sqrt{x}}
\end{align}\]
이다. 만약 \(x=0\)이면
\[\begin{align}
\lim_{\Delta x \rightarrow 0} \frac{f(x+\Delta x ) - f(x)}{\Delta x} = \lim_{\Delta x \rightarrow 0} \frac{\sqrt{\Delta x}}{\Delta x} = \lim_{\Delta x \rightarrow 0} \frac{1}{\sqrt{\Delta x}} = \infty
\end{align}\]
이다. 즉 \(f\)는 \(0\)에서 미분 불가능하다.
그러므로 \(f\)는 \((0,\,\infty)\)에서 미분 가능하며 도함수는 \[f ' (x) = \frac{1}{2\sqrt{x}}\] 이다. \(f\)의 도함수의 정의역이 \(f\)의 정의역의 진부분집합이라는 사실이 흥미롭다. - \(f(t)\)에 변수 \(x\)가 없다. 즉 \(x\)를 변수로 보았을 때 \(f(t)\)는 상수이다. 그러므로 \[\frac{d}{dx} f(t) =0\] 이다.
함수 \(f : D \rightarrow \mathbb{R}\)가 점 \(x_0 \in D\)에서 미분 가능하다고 하자. 그러면 \[\begin{align} \lim_{x\rightarrow x_0} f(x) &= \lim_{x\rightarrow x_0} ( f(x) - f(x_0 ) + f(x_0 ) ) \\[4pt] &= \lim_{x\rightarrow x_0} \left\{ \frac{f(x)-f(x_0 )}{x-x_0} (x-x_0 ) \right\} + f(x_0 ) \\[4pt] &= \lim_{x\rightarrow x_0} \left\{ \frac{f(x)-f(x_0 )}{x-x_0} \right\} \times \lim_{x\rightarrow x_0} (x-x_0 ) + f(x_0 ) \\[4pt] &= f ' (x_0 ) \times 0 + f(x_0) \\[5pt] &= f(x_0 ) \end{align}\] 이다. 즉 \(x_0\)에서 \(f\)의 극한값과 함숫값이 일치한다. 그러므로 \(f\)가 \(x_0\)에서 연속이다.
정리 5.1.1. (연속성과 미분 가능성의 관계)
함수 \(f\)가 점 \(x_0\)에서 미분 가능하면 \(f\)가 \(x_0\)에서 연속이다.
참고. 연속함수가 모두 미분 가능한 것은 아니다. 예컨대 함수 \(f:\mathbb{R} \rightarrow \mathbb{R}\)가 \[f(x) = \lvert x \rvert\]로 주어졌다면 \(f\)는 \(0\)에서 연속이지만 \(0\)에서 미분 불가능하다.
참고. \(f\)가 미분 가능하면 \(f\)가 연속이지만 \(f ' \)은 연속이 아닐 수 있다. 예컨대 함수 \(f:\mathbb{R} \rightarrow \mathbb{R}\)가 다음과 같이 주어졌다고 하자. \[f(x) = \begin{cases} x^2 \sin \frac{1}{x} & \quad \text{if} \quad x\ne 0 , \\[4pt] 0 & \quad \text{if} \quad x=0. \end{cases}\] 이 함수는 \(\mathbb{R}\)에서 미분 가능하지만 \(f ' \)은 \(0\)에서 연속이 아니다. 지금까지 다룬 내용만으로는 이 사실을 증명할 수 없지만 5장 4절까지 마친 후에는 이 사실을 증명할 수 있다. 도전!
이제 도함수의 도함수를 살펴보자. 함수 \(f\)가 \(x_0\)를 원소로 갖는 한 열린구간에서 미분 가능하고 \(f ' \)이 \(x_0\)에서 미분 가능하면 \(x_0\)에서 \(f ' \)의 미분계수를 다음과 같이 구할 수 있다. \[f ' ' (x_0 ) = \left. \frac{df ' }{dx} \right\vert_{x=x_0} = \lim_{\Delta x \rightarrow 0} \frac{f ' (x_0 + \Delta x) - f ' (x_0 )}{\Delta x}.\] 이 값을 \(x_0\)에서 \(f\)의 이계미분계수(second derivative)라고 부른다. \(x_0\)에서 \(f\)의 이계미분계수를 나타내는 기호는 다음과 같이 다양하다. \[\begin{gather} f^{(2)}(x_0) \quad\quad \frac{d^2}{(dx)^2} f(x_0 ) \quad\quad \frac{d^2 f}{(dx)^2} (x_0 ) \quad\quad \left. \frac{d^2 f}{(dx)^2} \right\vert_{x=x_0} \\[6pt] \left. \frac{d^2 y}{(dx)^2} \right\vert_{x=x_0} \quad\quad D^2 f(x_0 ) \quad\quad D^2 f \bigg\vert_{x=x_0} \end{gather}\] 같은 방법으로 \(n\)이 \(2\) 이상인 자연수일 때 \(x_0\)에서 \(f\)의 \(\boldsymbol{n}\)계미분계수를 정의할 수 있다. \(x_0\)에서 \(f\)의 \(n\)계미분계수를 나타내는 기호는 다음과 같이 다양하다. \[\begin{gather} f^{(n)} (x_0 ) \quad\quad \frac{d^n}{(dx)^n} f(x_0 ) \quad\quad \frac{d^n f}{(dx)^n} (x_0 ) \quad\quad \left. \frac{d^n f}{(dx)^n} \right\vert_{x=x_0} \\[6pt] \left. \frac{d^n y}{(dx)^n} \right\vert_{x=x_0} \quad\quad D^n f(x_0 ) \quad\quad D^n f \bigg\vert_{x=x_0} \end{gather}\]
보기 5.1.6. \(f(x)=x^3\)일 때 \(f\)의 \(n\)계미분계수는 다음과 같다. \[\begin{align} f ' (x) &= 3x^2 ,\\[5pt] f ' ' (x) &= 6x , \\[5pt] f ^{(3)} (x) &= 6 , \\[5pt] f^{(4)} (x) &= 0 , \\[5pt] f^{(5)} (x) &= 0 , \\[5pt] \quad\quad\vdots \\[5pt] f^{(n)} (x) & =0 \quad \text{for} \,\, n \ge 4. \end{align}\]
\(I\)가 길이가 양수인 구간이라고 하자. (길이가 무한대인 경우를 포함하자.) \(I\)의 모든 점에서 \(n\)계미분계수가 존재하는 실함수들의 모임을 \(D^{(n)} (I)\)로 나타낸다. 또한 \(I\)의 모든 점에서 연속인 \(n\)계도함수를 갖는 실함수들의 모임을 \(C^{(n)} (I)\)로 나타낸다.
만약 \(n=1\)이면 \(D^{(1)} (I)\)를 \(D(I)\)로 나타낸다. 즉 \(D(I)\)는 \(I\)에서 미분 가능한 실함수들의 모임이다. 만약 \(n=0\)이면 \(C^{(0)} (I)\)를 \(C(I)\)로 나타낸다. 즉 \(C(I)\)는 \(I\)에서 연속인 실함수들의 모임이다.