이 글은 『미적분학 첫걸음』 3장 3절의 내용입니다. (미적분학 첫걸음 차례 보기)
점 \(c\)에서 함수 \(f\)의 극한을 생각할 때, \(x\)가 \(c\)의 왼쪽으로부터 \(c\)에 다가가는 경우와 \(x\)가 \(c\)의 오른쪽으로부터 \(c\)에 다가가는 경우를 생각할 수 있다.
\(f:D \rightarrow \mathbb{R}\)가 함수이고 \(c\)가 \(D\)의 점이라고 하자.
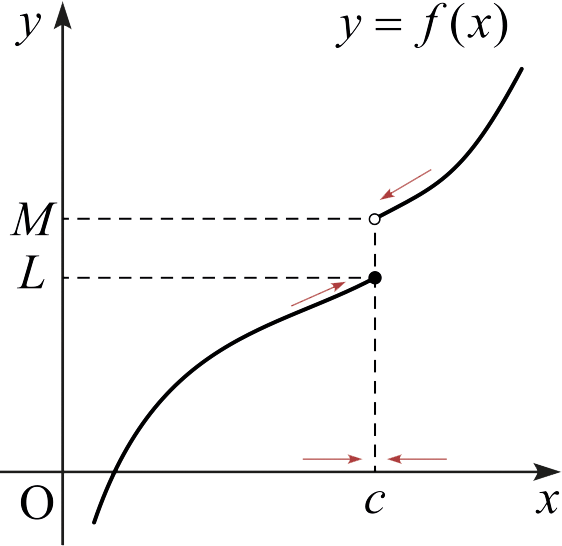
만약 \(x\)가 \(x < c\)를 유지한 채로 \(c\)에 다가갈 때 \(f(x)\)가 하나의 값 \(L\)에 다가가면, \(L\)을 \(c\)에서 \(f(x)\)의 좌극한(left-sided limit)이라고 부르고, 이 상황을 기호로 \[\lim_{x\rightarrow c^-} f(x) =L\] 또는 \[f(x) \rightarrow L \quad \text{as} \quad x \rightarrow c^-\] 와 같이 나타낸다.
만약 \(x\)가 \(c < x\)를 유지한 채로 \(c\)에 다가갈 때 \(f(x)\)가 하나의 값 \(M\)에 다가가면, \(M\)을 \(c\)에서 \(f(x)\)의 우극한(right-sided limit)이라고 부르고, 이 상황을 기호로 \[\lim_{x\rightarrow c^+} f(x) = M\] 또는 \[f(x) \rightarrow M \quad \text{as} \quad x \rightarrow c^+\] 와 같이 나타낸다.
좌극한과 우극한을 통틀어 한 방향 극한(one-sided limits)이라고 부른다.
\(c\)에서 \(f:D\rightarrow \mathbb{R}\)의 좌극한이 정의되려면 \(x\)가 \(D\)에 속하면서 \(c\)의 왼쪽에서 다가갈 수 있어야 한다. 즉 \(c\)가 \((-\infty ,\, c) \cap D\)의 집적점이어야 한다. 마찬가지로 \(c\)에서 \(f\)의 우극한이 정의되려면 \(c\)가 \((c,\,\infty ) \cap D\)의 집적점이어야 한다.
한 방향 극한이 발산하는 경우도 수렴하는 경우와 마찬가지 방법으로 정의한다.
보기 3.1.1.
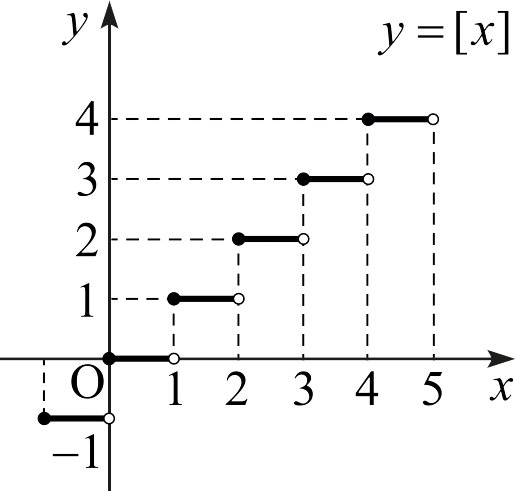
- \(f(x) = \lfloor x \rfloor\)이고 \(n\)이 정수라고 하자. 그러면 \[\lim_{x\rightarrow n^-} f(x) = n-1 \quad\text{and}\quad \lim_{x\rightarrow n^+} f(x)=n\] 이다. 만약 \(c\)가 정수가 아닌 실수라면 \[\lim_{x\rightarrow c^-} f(x) = \lim_{x\rightarrow c^+} f(x) = f(c)\] 이다.
- \(f(x) = \frac{1}{x}\)이면 \[\lim_{x\rightarrow 0^-} f(x) = -\infty \quad\text{and}\quad \lim_{x\rightarrow 0^+} f(x) = \infty\] 이다.
- \(p\)가 다항함수이고 \(c\)가 실수이면 \[\lim_{x\rightarrow c^-} p(x) = p(c) \quad\text{and}\quad \lim_{x\rightarrow c^+} p(x) = p(c)\] 이다.
- \(f(x) = \frac{\sin x}{x}\)이면 \[\lim_{x\rightarrow 0^-} f(x) = \infty \quad\text{and}\quad \lim_{x\rightarrow 0^+} f(x) = \infty\] 이다.
- \(f(x) = \sin \frac{1}{x}\)이면 \(0\)에서 \(f\)의 좌극한과 우극한은 모두 진동한다.
- \(\chi_\mathbb{Q} : \mathbb{R} \rightarrow \mathbb{R}\)가 \[\chi_\mathbb{Q} (x) = \begin{cases} 1 \quad & \text{if}\,\,x\in\mathbb{Q} , \\ 0 \quad & \text{if}\,\,x\notin\mathbb{Q} \end{cases}\] 로 정의된 특성함수(characteristic function)라면 임의의 점 \(c\)에서 \(\chi_\mathbb{Q}\)의 좌극한과 우극한은 모두 진동한다.
다음 정리는 한 방향 극한의 정의에 의하여 자명하게 성립한다. (증명은 상위 과정에서 하겠다.)
정리 3.3.1. (양 방향 극한과 한 방향 극한의 관계)
함수 \(f:D\rightarrow \mathbb{R}\)가 주어졌다고 하자. 그리고 \(c\)에서 \(f\)의 좌극한과 우극한이 정의된다고 하자. [즉 \(c\)가 \((-\infty ,\,c)\cap D\)의 집적점이며, \((c,\,\infty)\cap D\)의 집적점이다.] 이때 \[\lim_{x\rightarrow c} f(x) = L\] 이기 위한 필요충분조건은 \[\lim_{x\rightarrow c^-} f(x) = L \quad\text{and}\quad \lim_{x\rightarrow c^+} f(x)=L\] 인 것이다. 이것은 \(L\)이 실수일 때 뿐만 아니라, \(L = \infty\)이거나 \(L = -\infty\)일 때도 성립한다.
수열의 극한의 단조수렴 정리처럼 함수의 극한도 단조수렴을 생각할 수 있다.
함수 \(f\)가 열린구간 \(I=(a,\,b)\)에서 정의되었다고 하자. [물론 \(a < b\)라고 가정한다.] 그리고 \(f\)가 \(I\)에서 단조증가한다고 하자. 즉 임의의 \(s,\,t\in I\)에 대하여 \[s\le t \quad\Rightarrow\quad f(s) \le f(t)\] 가 성립한다고 하자.
이제 \(c\in I\)가 임의로 주어졌다고 하자.
“모든 \(x\in (a,\,c)\)에 대하여 \(f(x)\le L\)”
을 만족시키는 \(L\) 중에서 가장 작은 것을 택하자. 그러면 \(x\rightarrow c^-\)일 때 \(f(x)\)는 \(L\)에 수렴한다. 왜냐하면, 만약 \(f(x)\)가 \(L\)에 수렴하지 않는다면, “모든 \(x\in (a,\,c)\)에 대하여 \(f(x)\le L\)”을 만족시키는 더 작은 \(L\)을 택할 수 있기 때문이다.
마찬가지로 “모든 \(x\in (c,\,b)\)에 대하여 \(f(x)\ge M\)”을 만족시키는 가장 큰 \(M\)을 택하면 \(x\rightarrow c^+\)일 때 \(f(x)\)가 \(M\)에 수렴한다.
\(f\)가 \(I\)에서 단조감소한다고 하여도 같은 논법으로 \(c\)에서 \(f\)의 좌극한과 우극한이 모두 수렴한다는 결론을 끌어낼 수 있다.
이로써 다음 정리를 증명하였다.
정리 3.3.2. (단조수렴 정리)
\(I\)가 길이가 양수인 열린구간이라고 하자. 함수 \(f\)가 \(I\)에서 단조이면 \(I\)의 임의의 점에서 \(f\)의 좌극한과 우극한이 모두 수렴한다.
- 앞의 글 : 함수의 극한의 성질
- 다음 글 : 무한대를 포함한 극한
