이 글은 『미적분학 첫걸음』 2장 1절의 내용입니다. (미적분학 첫걸음 차례 보기)
무한급수의 뜻
\(\left\{ a_n\right\}\)이 무한수열이라고 하자. \(\left\{ a_n\right\}\)의 항을 순서대로 덧셈기호로 연결하여 나타낸 식 \[a_1 + a_2 + a_3 + \cdots\] 을 \(\left\{a_n\right\}\)의 무한급수(infinite series), 또는 간단히 급수(series)라고 부르고, 기호로 \[\sum_{n=1}^{\infty} a_n\] 과 같이 나타낸다. 이와 같은 정의에서 무한급수의 정의는 형식적(formal)이다. 즉 이 정의에서 무한급수는 식의 값이 아니라 식 그 자체를 나타낸다.
다음과 같은 합을 생각하자. \[S_n = \sum_{k=1}^n a_k = a_1 + a_2 + a_3 + \cdots + a_n .\] 그러면 임의의 양의 정수 \(n\)에 대하여 \(S_n\)이 정의되므로 \(\left\{S_n \right\}\)은 수열이다. 만약 \(\left\{S_n\right\}\)이 수렴하면, 즉 적당한 수 \(S\)에 대하여 \[\lim_{n\rightarrow\infty}\sum_{k=1}^{n} a_k = S\] 가 성립하면 \(S\)를 \(\left\{a_n\right\}\)의 무한급수의 합(sum)이라고 부르고, 이것을 기호로 \[\sum_{n=1}^{\infty} = S\] 와 같이 나타낸다. 이와 같은 맥락에서 \(\left\{ S_n \right\}\)을 \(\left\{a_n\right\}\)의 무한급수의 부분합(partial sum)이라고 부른다. \(S\)를 \(\left\{a_n\right\}\)의 무한급수의 값(value of series)이라고 부르기도 한다.
이로써 식 \[\sum_{n=1}^{\infty} a_n\] 은 서로 다른 두 가지를 동시에 나타낸다. 하나는 \(\left\{ a_n\right\}\)의 항을 순서대로 덧셈기호로 연결하여 나타낸 형식적 식을 나타내고, 다른 하나는 \(\left\{ a_n\right\}\)의 무한급수의 합을 나타낸다.
만약 \(n\rightarrow\infty\)일 때 부분합 \( S_n \)이 양의 무한대에 발산하거나 음의 무한대에 발산하면, 이것을 기호로 각각 \[\sum_{n=1}^{\infty} a_n = \infty\] 또는 \[\sum_{n=1}^{\infty} a_n = -\infty\] 와 같이 나타낸다.
예제 2.1.1. 다음 무한급수의 수렴 여부를 조사하고, 수렴하는 경우 그 합을 구하시오. \[\sum_{n=1}^{\infty} \frac{1}{(n+1)(n+2)}\] 풀이. \(n\ge 2\)일 때 \[\begin{align} S_n &= \sum_{k=1}^n \frac{1}{(k+1)(k+2)} \\[5pt] &= \left( \frac{1}{2} - \frac{1}{3}\right) + \left(\frac{1}{3} - \frac{1}{4} \right) + \left(\frac{1}{4} - \frac{1}{5}\right) + \cdots + \left( \frac{1}{n+1} - \frac{1}{n+2} \right) \\[5pt] &= \frac{1}{2} - \frac{1}{n+2} \end{align}\] 이다. 따라서 \[\lim_{n\rightarrow\infty} S_n = \lim_{n\rightarrow\infty}\left( \frac{1}{2} - \frac{1}{n+2} \right) = \frac{1}{2}\] 이다. 그러므로 문제에서 주어진 무한급수는 수렴하며, 그 합은 \(\frac{1}{2}\)이다.
예제 2.1.2. 다음 무한급수의 수렴 여부를 조사하고, 수렴하는 경우 그 합을 구하시오. \[\sum_{n=1}^{\infty} \frac{1}{\sqrt{n+1} + \sqrt{n}}\] 풀이. 주어진 무한급수의 일반항을 변형하면 \[\frac{1}{\sqrt{n+1} + \sqrt{n}} = \frac{\sqrt{n+1} - \sqrt{n}}{ \left(\sqrt{n+1} + \sqrt{n}\right)\left(\sqrt{n+1} - \sqrt{n}\right) } = \sqrt{n+1} - \sqrt{n}.\] 이 식을 이용하여 부분합을 구하면 다음과 같다. \[\begin{align} S_n &= \sum_{k=1}^{n} \frac{1}{\sqrt{k+1}+\sqrt{k}} \\[5pt] &= \sum_{k=1}^{n} \left( \sqrt{k+1} - \sqrt{k} \right) \\[5pt] &= \left( \sqrt{2} - \sqrt{1} \right) + \left( \sqrt{3} - \sqrt{2} \right) + \left( \sqrt{4} - \sqrt{3} \right) + \cdots + \left(\sqrt{n+1} - \sqrt{n}\right)\\[5pt] &= \sqrt{n+1} - 1. \end{align}\] 따라서 \[\lim_{n\rightarrow\infty} S_n = \lim_{n\rightarrow\infty} \left(\sqrt{n+1} - 1\right) = \infty\] 이다. 그러므로 문제에서 주어진 무한급수는 양의 무한대로 발산한다.
무한급수의 계산
무한급수의 부분합은 수열이며 무한급수는 부분합의 극한이므로, 수열의 극한의 성질로부터 무한급수의 성질을 얻을 수 있다.
정리 2.1.1. 두 무한급수 \[\sum_{n=1}^{\infty} a_n ,\quad \sum_{n=1}^{\infty} b_n\] 이 모두 수렴하고, 그 합이 각각 \(S,\) \(T\)라고 하자. 그러면 다음이 성립한다.
- \(\sum_{n=1}^{\infty} \left( ka_n \right) = kS .\) (단, \(k\)는 상수.)
- \(\sum_{n=1}^{\infty} \left( a_n + b_n \right) = S+T.\)
- \(\sum_{n=1}^{\infty} \left( a_n - b_n \right) = S-T.\)
예제 2.1.3. \(\sum_{n=1}^{\infty} a_n = 3 ,\) \(\sum_{n=1}^{\infty} b_n = -4\)일 때 다음 무한급수의 합을 구하시오.
- \(\sum_{n=1}^{\infty} \left(3a_n - b_n \right)\)
- \(\sum_{n=1}^{\infty} \left(2a_n + 5b_n \right)\)
풀이.
- \[\begin{align}\sum_{n=1}^{\infty} \left(3a_n - b_n \right) &= 3\times\sum_{n=1}^{\infty} a_n - \sum_{n=1}^{\infty}b_n \\[5pt] &= 3\times 3 - (-4) = 13. \end{align}\]
- \[\begin{align}\sum_{n=1}^{\infty} \left(2a_n + 5b_n \right) &= 2\times\sum_{n=1}^{\infty} a_n + 5\times\sum_{n=1}^{\infty} b_n \\[5pt] &= 2 \times 3 + 5 \times (-4) = -14. \end{align}\]
무한급수 \[\sum_{n=1}^{\infty} a_n\] 이 수렴하고, 그 합이 \(S\)라고 하자. 일반항 \(\left\{a_n \right\}\)의 극한을 계산하면 다음과 같다. \[\begin{align} \lim_{n\rightarrow\infty} a_n &= \lim_{n\rightarrow\infty}\left( \sum_{k=1}^{n} a_k - \sum_{k=1}^{n-1} a_k \right) \\[5pt] &= \lim_{n\rightarrow\infty}\sum_{k=1}^n - \lim_{n\rightarrow\infty}\sum_{k=1}^{n-1}a_k = S-S =0.\end{align}\] 그러므로 다음 정리를 얻는다.
정리 2.1.2. (일반항 판정법)
무한급수 \(\sum_{n=1}^{\infty} a_n\)이 수렴하면 일반항 \(\left\{ a_n \right\}\)이 \(0\)에 수렴한다.
보기 2.1.4. 무한급수 \[\sum_{n=1}^{\infty} (-1)^n\] 은 발산한다. 왜냐하면 \(n\rightarrow\infty\)일 때 \((-1)^n\)이 \(0\)에 수렴하지 않기 때문이다.
참고. 정리 2.1.2의 역은 참이 아니다. 예컨대 \(n\rightarrow\infty\)일 때 \[\frac{1}{\sqrt{n+1} + \sqrt{n}} \,\rightarrow\,0\] 이지만 무한급수 \[\sum_{n=1}^{\infty} \frac{1}{\sqrt{n+1} + \sqrt{n}}\] 은 양의 무한대로 발산한다.
무한등비급수
등비수열의 무한급수를 무한등비급수 또는 간단히 등비급수 또는 기하급수(geometric series)라고 부른다.
수열 \(\left\{ a_n \right\}\)이 \[a_n = ar^{n-1} ,\,\, a\ne 0\] 으로 주어진 등비수열이라고 하자. \(\left\{ a_n \right\}\)의 급수의 부분합을 구하면 \(r\ne 1\)일 때 \[S_n = \sum_{k=1}^n ar^{k-1} = \frac{a(1-r^n )}{1-r}\] 이고, \(r = 1\)일 때 \[S_n = \sum_{k=1}^n ar^{k-1} = na\] 이다. 그러므로 부분합의 극한 \[\lim_{n\rightarrow\infty} S_n\] 이 수렴할 필요충분조건은 \(\lvert r \rvert < 1\)이다.
정리 2.1.3. (무한등비급수의 합)
\(a\ne 0\)일 때, 무한등비급수 \[\sum_{n=1}^{\infty} ar^{n-1}\] 이 수렴할 필요충분조건은 \(\lvert r \rvert < 1\)인 것이다. 이 무한급수가 수렴할 때 그 합은 \[\frac{a}{1-r}\] 이다.
예제 2.1.5. 다음 무한급수의 합을 구하시오.
- \(1 + \frac{2}{3} + \left( \frac{2}{3} \right)^2 + \left( \frac{2}{3} \right)^3 + \cdots \)
- \(1 - \frac{4}{3} + \left( \frac{4}{3}\right)^2 - \left(\frac{4}{3}\right)^3 + - \cdots \)
풀이.
- 문제에서 주어진 무한급수는 일반항의 공비가 \(\frac{2}{3}\)인 무한등비급수이다. 공비의 절댓값이 \(1\)보다 작으므로 이 무한급수는 수렴하며 그 합은 \[\frac{1}{1-\frac{2}{3}} = 3\] 이다.
- 문제에서 주어진 무한급수는 일반항의 공비가 \(-\frac{4}{3}\)인 무한등비급수이다. 공비의 절댓값이 \(1\)보다 크므로 이 무한급수는 발산한다.
예제 2.1.6. 다음 무한급수의 합을 구하시오.
- \(\displaystyle\sum_{n=1}^{\infty}\frac{3^n + 4^n}{5^n}\)
- \(\displaystyle\sum_{n=1}^{\infty}\frac{(-2)^n + 5^n}{(-6)^n}\)
풀이.
- \[\begin{align} \sum_{n=1}^{\infty} \frac{3^n + 4^n}{5^n} &= \sum_{n=1}^{\infty}\left(\frac{3}{5}\right)^n + \sum_{n=1}^{\infty}\left(\frac{4}{5}\right)^n \\[5pt] &= \frac{\frac{3}{5}}{1-\frac{3}{5}} + \frac{\frac{4}{5}}{1-\frac{4}{5}} = \frac{3}{2} + \frac{4}{1} = \frac{11}{2}. \end{align}\]
- \[\begin{align} \sum_{n=1}^{\infty} \frac{(-2)^n + 5^n}{(-6)^n} &= \sum_{n=1}^{\infty}\left(\frac{-2}{-6}\right)^n + \sum_{n=1}^{\infty}\left(\frac{5}{-6}\right)^n \\[5pt] &= \frac{\frac{1}{3}}{1-\frac{1}{3}} + \frac{-\frac{5}{6}}{1-\left(-\frac{5}{6}\right)} = \frac{1}{2} + \left(-\frac{5}{11}\right) = \frac{1}{22}. \end{align}\]
예제 2.1.7. 무한등비급수의 합을 이용하여 다음 순환소수를 분수로 나타내시오.
- \(0.0 \dot{1} \dot{2}\)
- \(1. \dot{0} 1 \dot{2}\)
풀이.
- \[\begin{align} 0.0 \dot{1} \dot{2} &= \frac{12}{10^3} + \frac{12}{10^5} + \frac{12}{10^7} + \cdots \\[5pt] &= \frac{12}{10^3} \times \frac{1}{1-\frac{1}{100}} = \frac{12}{1000} \times \frac{100}{99} = \frac{2}{165}. \end{align}\]
- \[\begin{align} 1. \dot{0} 1 \dot{2} &= 1+ \frac{12}{1000} + \frac{12}{1000^2} + \frac{12}{1000^3} + \cdots \\[5pt] &= 1+12\times \frac{\frac{1}{1000}}{1-\frac{1}{1000}} = 1+12 \times \frac{1}{999} = \frac{337}{333}. \end{align}\]
예제 2.1.8. 그림과 같이 한 변의 길이가 \(4\)인 정사각형을 크기가 같은 \(4\)개의 정사각형으로 쪼갠 뒤 그 중 한 조각에 색을 칠한다. 색이 칠해지지 않은 \(3\)개의 정사각형 조각 중 하나를 택하여 크기가 같은 \(4\)개의 정사각형으로 쪼갠 뒤 그 중 한 조각에 색을 칠한다. 이와 같은 과정을 무한히 반복할 때, 색이 칠해진 정사각형 조각의 넓이의 합을 구하시오.
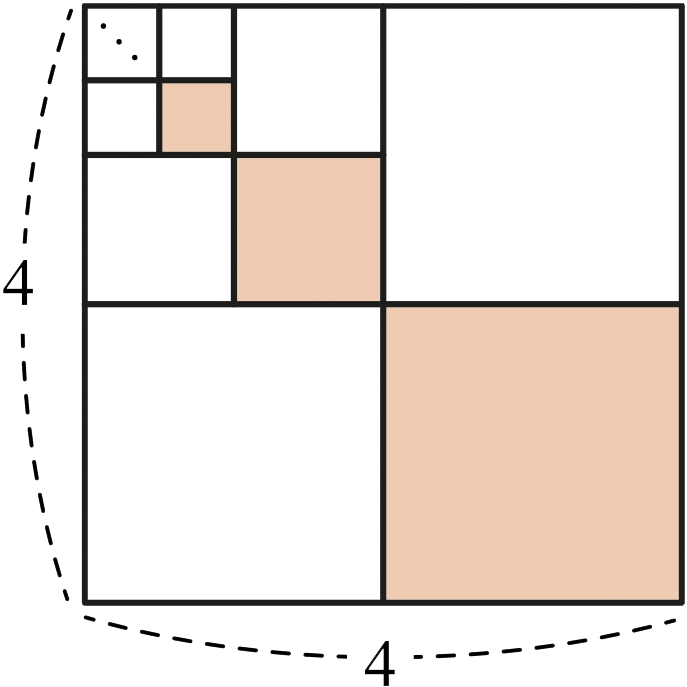
풀이. 그림과 같이 색칠된 정사각형의 넓이를 큰 정사각형부터 차례로 \(S_1 ,\) \(S_2 ,\) \(S_3 ,\) \(\cdots\)라고 하자.
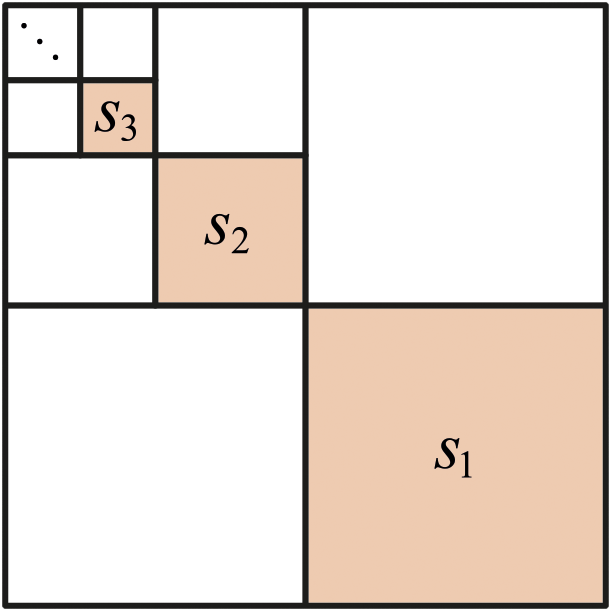
그러면 \(\left\{S_n\right\}\)은 등비수열이다. \[\begin{align} S_1 &= 16\times\frac{1}{4} = 4 ,\\[5pt] S_2 &= S_1 \times \frac{1}{4} = 1 ,\\[5pt] S_3 &= S_2 \times \frac{1}{4} = \frac{1}{4}, \\[5pt] S_4 &= S_3 \times \frac{1}{4} = \left(\frac{1}{4}\right)^2 ,\\[5pt] &\,\,\vdots \end{align}\] 그러므로 무한등비급수의 합 공식에 의하여, 색칠된 정사각형의 넓이의 합은 \[\sum_{n=1}^{\infty}S_n = \frac{4}{1-\frac{1}{4}} = \frac{16}{3}\] 이다.
