체 \(K\) 위에서 정의되어 있고 차원이 \(n\)인 유한차원 벡터공간은 \(K^n\)와 동형이다. 그러므로 유한차원 벡터공간 사이에서 정의된 선형변환은 적당한 \(n,\) \(m\)에 대하여 선형변환 \(T : K^n \rightarrow K^m\)과 같은 것으로 생각할 수 있다. 더욱이 \(T : K^n \rightarrow K^m\)은 행렬로 나타낼 수 있으므로 유한차원 벡터공간 사이에 정의된 선형변환은 행렬과 동일시할 수 있다. 그런데 이러한 행렬 표현은 벡터공간에 어떠한 기저가 주어졌는지에 따라 달라진다.
이 포스트에서는 유한차원 벡터공간 사이에서 정의된 선형변환을 행렬로 나타내고, 기저가 바뀌었을 때 선형변환을 표현하는 행렬이 어떻게 바뀌는지 살펴본다.
선형변환의 공간
\(V\)와 \(W\)가 \(K\) 위에서의 벡터공간이라고 하자. 이때 \(V\)로부터 \(W\)로의 선형변환들의 모임을 \(\Hom(V,\,W)\)로 나타낸다. 만약 \(f,\,g\in\Hom(V,\,W)\)와 \(\lambda\in K\)에 대하여 \(\lambda f\)와 \(f+g\)를 \[\begin{align} (\lambda f)(v) &= \lambda (f(v)) \,\text{ for all } v\in V ,\\[5pt] (f+g)(v) &= f(v) + g(v) \,\text{ for all } v\in V \end{align}\] 를 만족시키는 함수로 정의하면, 이러한 연산이 주어진 집합 \(\Hom(V,\,W)\)는 벡터공간이 된다.
\(U,\) \(V,\) \(W\)가 \(K\) 위에서의 벡터공간이라고 하자. 그러면 다음이 성립한다.
- \(g\in\Hom (V,\,W),\) \(f_1 ,\,f_2 \in \Hom (U,\,V)\)에 대하여\[g\circ (f_1 + f_2 ) =g\circ f_1 + g\circ f_2 .\]
- \(g_1 ,\, g_2 \in\Hom(V,\,W),\) \(f\in\Hom (U,\,V)\)에 대하여\[(g_1 + g_2 ) \circ f = g_1 \circ f + g_2 \circ f .\]
- \(g\in\Hom (V,\,W),\) \(f\in\Hom(U,\,V),\) \(\lambda\in K\)에 대하여\[(\lambda g)\circ f = g\circ (\lambda f) = \lambda (g\circ f).\]
특히 \(f,\,g\in\Hom(V,\,V)\)와 \(\lambda\in K\)에 대하여 다음이 성립한다. \[(\lambda g) \circ f = g\circ (\lambda f) = \lambda (g\circ f).\tag{1.1}\] \(K\) 위에서 정의된 벡터공간에 환의 조건을 만족시키는 곱 연산이 주어져 있고 식 (1.1)을 만족시킬 때, 그러한 공간을 K-대수(K-algebra)라고 부른다. 이와 같은 관점에서 \(\Hom(V,\,V)\)는 스칼라곱, 벡터합, 곱 연산(함수합성)이 주어진 K-대수이다.
정리 1. \(f,\,g\in \Hom(V,\,W)\)라고 하자. 만약 \(S\)가 \(V\)를 생성하는 집합이고, \(S\)의 모든 원소에 대하여 \(f\)와 \(g\)의 함숫값이 일치하면 \(f\)와 \(g\)는 같은 함수이다.
증명.
\(v\in V\)가 임의로 주어졌다고 하자. 그러면 \(S\)의 원소 \(v_1 ,\) \(v_2 ,\) \(\cdots ,\) \(v_n\)과 스칼라 \(\lambda_j\)들이 존재하여 \[v = \sum_{j=1}^n \lambda_j v_j\] 이다. 그런데 \(f\)와 \(g\)가 선형이므로 다음이 성립한다. \[\begin{align} f(v) &= f \left( \sum_{j=1}^n \lambda_j v_j \right) = \sum_{j=1}^n \lambda_j f( v_j) \\[5pt] &= \sum_{j=1}^n \lambda_j g( v_j) = g \left( \sum_{j=1}^n \lambda_j v_j \right) = g(v). \end{align}\] 그러므로 \(V\) 위에서 \(f=g\)이다.
\(\Hom(K^n ,\, K^m )\)의 표현
이제 유한차원 벡터공간 사이에 정의된 선형변환과 행렬 사이의 관계를 살펴보자.
\(T \in\Hom (K^n ,\, K^m )\)이라고 하자. 이때 행렬 \(M(T) \in \Mat_{m\times n} (K)\)를 \(j\)째 열벡터가 \(T(\mathbf{e}_j )\)인 행렬로 정의한다. 행렬 \(M(T)\)를 표준기저에 대한 \(T\)의 표현행렬이라고 부른다.
보기 1. 다음과 같이 정의된 선형변환 \(T : \mathbb{R}^3 \rightarrow \mathbb{R}^2\)를 생각하자. \[T : \left(\begin{array}{} x_1 \\ x_2 \\ x_3 \end{array}\right) \mapsto \left(\begin{array}{} 2x_1 +x_3 \\ x_2 - x_3 \end{array}\right).\tag{2.1}\] 그러면 \[\begin{align} T(\mathbf{e}_1) &= \left(\begin{array}{} 2 \\ 0 \end{array}\right), \\[5pt] T(\mathbf{e}_2) &= \left(\begin{array}{} 0 \\ 1 \end{array}\right), \\[5pt] T(\mathbf{e}_3) &= \left(\begin{array}{r} 1 \\ -1 \end{array}\right) \end{align}\] 이므로 \[M(T) = \left(\begin{array}{ccr} 2 & 0 & 1 \\ 0 & 1 & -1 \end{array}\right).\tag{2.2}\] 이다.
위 예제에서는 (2.1)과 같이 정의된 선형변환으로부터 (2.2)의 행렬을 얻었다. 역으로 (2.2)와 같은 행렬이 주어졌다면 \[ T : \left(\begin{array}{} x_1 \\ x_2 \\ x_3 \end{array}\right) \mapsto \left(\begin{array}{ccr} 2 & 0 & 1 \\ 0 & 1 & -1 \end{array}\right) \left(\begin{array}{} x_1 \\ x_2 \\ x_3 \end{array}\right) \] 과 같이 행렬을 왼쪽에 곱함으로써 (2.1)과 같은 선형변환을 얻는다.
이와 같은 내용을 일반화하면 다음 정리를 얻는다.
정리 2. 선형변환 \(T\in\Hom (K^n ,\, K^m )\)과 행렬 \(M(T)\in\Mat_{m\times n} (K)\)를 대응시키는 함수는 동형사상이며, 이러한 관점에서 \(\Hom (K^n ,\, K^m )\)과 \(\Mat_{m\times n} (K)\)는 동형이다.
정리 2는 다른 방법으로 표현할 수 있다. 행렬 \(A\in\Mat_{m\times n} (K)\)에 대응되는 선형변환을 \(T_A\)로 나타내자. 그러면 \[M(T_A) = A\tag{2.3}\] 가 성립한다. 역으로 임의의 \(T\in\Hom (K^n ,\, K^m )\)에 대하여 \[T_{M(T)} = T\tag{2.4}\] 가 성립한다. 그러므로 지금부터는 \(K^n\)으로부터 \(K^m\)으로의 선형변환은 \(m\times n\) 행렬과 같은 것으로 여겨도 좋다. (\(m\)과 \(n\)의 순서를 주의하자.)
정리 2로부터 자연스럽게 다음 결과를 얻는다.
따름정리 3. \(\Hom(K^n ,\, K^m )\)의 차원은 \(mn\)이다.
선형변환의 합성은 행렬의 곱으로 표현할 수 있다. 이 내용을 더 자세히 살펴보자. \[A\in\Mat_{m\times n}(K) ,\,\, B\in\Mat_{n\times p} (K)\] 라고 하자. 그러면 \(T_{AB}\)와 \(T_A \circ T_B\)는 모두 \(\Hom(K^p ,\, K^m )\)에 속한다. 그런데 \[T_{AB}(\mathbf{e}_j) = (AB)\mathbf{e}_j = (AB)^j\tag{2.5}\] 이고 \[\begin{align} (T_A \circ T_B )(\mathbf{e}_j) &= T_A (T_B (\mathbf{e}_j )) = T_A(B\mathbf{e}_j) \\[5pt] &= T_A(B^j ) = A\cdot B^j\tag{2.6}\end{align}\] 이다. 그런데 (2.5)와 (2.6)은 모두 \(AB\)의 \(j\)째 열벡터와 같다. 그러므로 다음 결과를 얻는다.
정리 4. \(A\in\Mat_{m\times n}(K) ,\) \(B\in\Mat_{n\times p} (K)\)에 대하여 다음이 성립한다.
\[T_{AB} = T_A \circ T_B .\]즉 선형변환의 합성은 행렬의 곱과 같다. 그런데 함수의 합성의 결합법칙이 성립하므로 다음을 얻는다.
따름정리 5. 행렬의 곱의 결합법칙이 성립한다.
이 따름정리는 다음과 같이 나타낼 수도 있다.
따름정리 6. \(T : K^p \rightarrow K^n \)과 \(T ' : K^n \rightarrow K^m\)이 선형변환이면 다음이 성립한다.
\[M(T ' \circ T ) = M(T ' ) M(T) .\]보기 2. \(V = \mathbb{R}^2\)이고 \(T_\theta\)가 원점을 중심으로 시계 반대방향으로 \(\theta\)만큼 회전하는 변환이라고 하자. 두 표준기지원소를 \(\theta\)만큼 회전한 결과는 다음과 같다. \[\begin{align} T_\theta(\mathbf{e}_1) &= (\cos\theta ,\, \sin\theta ), \\[5pt] T_\theta(\mathbf{e}_2) &= ( -\sin\theta ,\, \cos\theta ). \end{align}\] 그러므로 \(T_\theta\)의 표현행렬은 다음과 같다. \[M(T_\theta ) = \left(\begin{array}{cr} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{array}\right).\] 원점을 중심으로 \(\beta\)만큼 회전한 후 \(\alpha\)만큼 더 회전하는 것은 원점을 중심으로 \(\alpha+\beta\)만큼 회전하는 것과 같으므로 \[T_{\alpha+\beta} = T_\alpha \circ T_\beta\] 이다. 그러므로 \[M(T_{\alpha+\beta} ) = M(T_\alpha)M(T_\beta)\] 이다. 이 등식을 행렬로 나타내면 다음과 같다. \[ \left(\begin{array}{cr} \cos(\alpha+\beta) & -\sin(\alpha+\beta) \\ \sin(\alpha+\beta) & \cos(\alpha+\beta) \end{array}\right) = \left(\begin{array}{cr} \cos\alpha & -\sin\alpha \\ \sin\alpha & \cos\alpha \end{array}\right) \left(\begin{array}{cr} \cos\beta & -\sin\beta \\ \sin\beta & \cos\beta \end{array}\right)\] 등식의 우변의 행렬곱을 풀어서 계산하면 다음과 같은 삼각함수의 덧셈 정리를 얻는다. \[\begin{align} \cos(\alpha+\beta) &= \cos\alpha \cos\beta - \sin\alpha \sin\beta , \\[5pt] \sin(\alpha+\beta) &= \sin\alpha \cos\beta + \cos\alpha \sin\beta . \end{align}\]
\(\Hom(V ,\, V ' )\)의 표현
지금부터 다루는 벡터공간은 별다른 언급이 없는 한 유한차원인 것으로 약속하자.
\(V\)가 \(n\)차원 벡터공간이고 \(B = \left\{ v_1 ,\, \cdots ,\, v_n \right\}\)이 \(V\)의 기저라고 하자. 그러면 좌표함수 \(\gamma_B : V \rightarrow K^n\)은 \[\gamma_B \left( \sum_{j=1}^n \lambda_j v_j \right) =(\lambda_1 ,\, \cdots ,\, \lambda_n )\] 으로 정의된 동형사상이다. 마찬가지로 \(V ' \)이 \(m\)차원 벡터공간일 때 좌표함수 \(\gamma_{B ' } : V ' \rightarrow K^m\)은 동형사상이다.
이때 \(V\)로부터 \(V ' \)으로의 선형변환 \(T : V \rightarrow V ' \)은 \(K^n\)으로부터 \(K^m\)으로의 선형변환 \[\gamma_{B ' } \circ T \circ \gamma_B ^{-1} : K^n \rightarrow K^m \tag{3.1}\] 에 대응된다. 이러한 선형변환의 표현행렬을 기저 \(B,\) \(B ' \)에 대한 \(T\)의 표현행렬이라고 부르고 \(M_{B,B ' } (T)\)로 나타낸다.
선형변환 \(T : V \rightarrow V ' \)을 (3.1)에 대응시키는 함수는 일대일대응이며 동형사상이다. 이러한 관점에서 \(\Hom(V ,\, V ' )\)과 \(\Hom(K^n ,\, K^m )\)은 동형이다. 더욱이 \(\Hom(K^n ,\, K^m )\)의 성질로부터 \(\Hom(V ,\, V ' )\)의 성질을 끌어낼 수 있다.
- \(V\)와 \(V ' \)이 각각 \(n\)차원, \(m\)차원 벡터공간이면 \(\Hom(V,\,V ' )\)은 \(mn\)차원 벡터공간이다.
- \(T : V \rightarrow V ' \)과 \(T ' : V ' \rightarrow V '' \)이 선형변환이면 \(T ' \circ T\)의 표현행렬은 다음과 같다.\[M_{B,B ' } (T ' \circ T ) = M_{B ', B ' '} (T ' ) M_{B,B '} (T ).\]
\(V\)가 \(n\)차원 벡터공간인 경우 \(\Hom(V,\,V)\)는 \(\Hom(K^n ,\, K^n)\)과 동형이다. 그런데 \(\Hom(K^n ,\, K^n)\)이 K-대수이므로 \(\Hom(V,\,V)\)도 K-대수이다. \(V\)의 기저 \(B\)를 고정시키고 \(M_{B,B}(T)\)를 간단히 \(M_B(T)\)로 나타내자. 그러면 \(T\in\Hom(V,\,V)\)를 \(\gamma_B \circ T \circ \gamma_B^{-1} \in \Hom(K^n ,\, K^n)\)에 대응시키는 함수는 벡터동형사상이며 함수의 합성을 보존한다. 그러므로 \(\Hom(V,\,V)\)와 \(\Hom(K^n,\,K^n)\)은 K-대수 동형이다.
보기 3. \(V\)가 \(\sin x\)와 \(\cos x\)에 의하여 생성되는 연속함수공간이라고 하자. \(\sin x\)와 \(\cos x\)은 그 자체로서 \(V\)의 기저가 된다. \(D\)가 미분연산자라고 하자. 그러면 \[\begin{align} D(\sin x) &= 0 \cdot \sin x + 1 \cdot \cos x ,\\[5pt] D(\cos x) &= -1 \cdot \sin x + 0 \cdot \cos x \end{align}\] 이므로 \(D\)의 표현행렬은 다음과 같다. \[A = \left(\begin{array}{cr} 0 & -1 \\ 1 & 0 \end{array}\right).\] 만약 \(f(x) = 2\sin x + 5\cos x\)이면 \(f\)는 순서쌍 \((2,\,5)\)로 나타낼 수 있는 벡터이고 \[\left(\begin{array}{cr} 0 & -1 \\ 1 & 0 \end{array}\right) \left(\begin{array}{} 2\\5 \end{array}\right) = \left(\begin{array}{r} -5\\2 \end{array}\right)\] 이므로 \(Df\)는 다음과 같다. \[D(f(x)) = f ' (x) = -5 \sin x + 2 \cos x\] 한편 \(D^2 = D \circ D\)이므로 \(D^2\)의 표현행렬은 다음과 같다. \[A^2 = \left(\begin{array}{rr} -1 & 0 \\ 0 & -1 \end{array}\right).\] 같은 방법으로 \(D^4\)의 표현행렬을 구하면 \(A^4 = A^2 A^2 = I_2\)를 얻는다.
쌍대공간
\(V\)가 \(K\) 위에서의 벡터공간이라고 하자. \(K\)는 체이지만 1차원 벡터공간이기도 하다. 이때 \(V\)로부터 \(K\)로의 선형변환들의 모임을 \(V^*\)로 나타내고 \(V\)의 쌍대공간(dual space)이라고 부른다. 즉 \(V^* = \Hom(V,\,K)\)이다. 그리고 \(V^*\)의 원소를 선형범함수(linear functional)라고 부른다. \(V\)가 \(n\)차원 벡터공간이면 \(V^*\) 또한 \(n\)차원 벡터공간이다. (참고: 쌍대공간의 기저)
쌍대공간의 정의만 보았을 땐 그다지 쓸모있어 보이지 않는다. 하지만 쌍대공간은 행렬의 행공간의 성질과 열공간의 성질을 이어주는 역할을 한다. 지금부터 그 과정을 살펴보자.
\(V,\) \(W\)가 유한차원 벡터공간이고 선형변환 \(T : V \rightarrow W\)가 주어졌다고 하자. 이때 \(V\)와 \(W\)의 쌍대공간을 생각할 수 있는 것처럼 \(T\)에 대응되는 선형변환 \(T^*\)를 생각할 수 있다. \(T\)는 벡터를 벡터에 대응시키는 변환이지만 \(T^*\)는 범함수를 범함수에 대응시키는 변환이어야 한다. \(f\in W^*\)가 주어졌다고 하자. 이때 \(f\)를 \(f\circ T\)에 대응시키는 함수 \[T^* : W^* \rightarrow V^* ,\,\, f\mapsto f\circ T\] 를 \(T\)의 전치함수(transpose map)라고 부른다. 전치함수는 다음과 같은 성질을 가진다.
- \(K\) 위에서의 벡터공간 \(V\)에 대하여 \((1_V)^* = 1_{V^*}\)이다. 즉 전치함수는 항등함수를 항등함수에 대응시킨다.
- \(T_1\)과 \(T_2\)가 \(K\) 위에서 정의된 벡터공간 위에서의 선형변환이고 \(T_1 \circ T_2\)가 정의되면 다음이 성립한다. \[(T_1 \circ T_2 )^* = T_2 ^* \circ T_1 ^* .\] 이와 같은 성질을 반변성질(contravariance)이라고 부른다.
더욱이 \(T\)의 대응 성질과 \(T^*\)의 대응 성질은 다음과 같은 관계를 가진다.
- \(T\)가 위로의 함수이면 \(T^*\)는 일대일 함수이다.
- \(T\)가 일대일 함수이면 \(T^*\)는 위로의 함수이다.
- \(T\)가 일대일 대응이면 \(T^*\)도 일대일 대응이다.
이러한 성질의 따름정리로서 다음 정리를 얻는다.
정리 5. \(V\)와 \(W\)가 \(K\) 위에서의 유한차원 벡터공간이고 \(T : V \rightarrow W\)가 선형변환이면 다음이 성립한다. \[\operatorname{rk}(T) = \operatorname{rk}(T^* ).\] 즉 \(T\)의 상(image)의 차원과 \(T^*\)의 상의 차원이 같다.
증명.
\(T\)가 위로의 함수인 경우부터 살펴보자. 그러면 \(\operatorname{Im} (T) = W\)이고 \(\operatorname{rk}(T) = \dim(W)\)이다. \(T^* : W^* \rightarrow V^*\)가 일대일 함수이므로 \(T^*\)의 핵의 차원은 \(0\)이다. 그러므로 Rank-Nullity 정리에 의하여 \(\operatorname{rk}(T^*) = \dim(W^*)\)이다. 그런데 \(\dim(W^*) = \dim(W)\)이므로 \[\operatorname{rk}(T) = \dim(W) = \dim(W^*) = \operatorname{rk}(T^*)\]이다.
다음으로 \(T\)가 일반적인 선형변환인 경우를 살펴보자. \(T\)가 위로의 함수가 아닐 수 있기 때문에, \(T\)와 같은 역할을 하는 위로의 함수 \(T_1\)을 구성해야 한다. \(\operatorname{Im}(T) = W_1\)이라고 하자. 그러면 포함사상 \(i : W_1 \rightarrow W\)에 대하여 \(i\circ T_1\)은 \(V\)로부터 \(W\)로의 함수이고 \[T = i\circ T_1\] 이 성립한다. 여기서 \(T_1\)은 \(T\)와 동일하게 대응시키는 함수이고 위로의 함수이며 \(\operatorname{rk}(T) = \dim(W_1)= \operatorname{rk}(T_1)\)이다. \(T,\) \(T_1,\) \(i\)의 전치함수를 생각하면 \(T^*\)와 \(T_1^* \circ i^*\)는 모두 \(W^*\)로부터 \(V^*\)로의 함수이고 \[T_1^* \circ i^* = T^*\] 이다. 그런데 \(i^*\)가 위로의 함수이므로 \(T^*\)와 \(T_1^*\)는 같은 상을 가지며, 같은 계수를 가진다. 그러므로 \[\operatorname{rk}(T) = \operatorname{rk}(T_1) \,\text{ and }\, \operatorname{rk}(T^*) = \operatorname{rk}(T_1 ^*)\] 이다. 그런데 \(T_1\)이 위로의 함수이므로 \[\operatorname{rk}(T_1) = \operatorname{rk}(T_1 ^*)\] 이다. 그러므로 \(\operatorname{rk}(T) = \operatorname{rk}(T^* )\)이다.
\(B_1 = \left\{ v_1 ,\, \cdots ,\, v_n \right\}\)이 \(V\)의 기저이고 \(B_2 = \left\{ w_1 ,\, \cdots ,\, w_m \right\}\)이 \(V_2\)의 기저라고 하자. 이 두 기저의 쌍대기저를 \(B_1 ^* ,\) \(B_2 ^*\)로 나타내자. 이때 전치함수 \(T^*\)의 표현행렬은 선형변환 \(T\)의 표현행렬을 이용하여 다음과 같이 쉽게 구할 수 있다.
정리 6. 기저 \(B_1 ,\) \(B_2\)에 대한 선형변환 \(T:V_1 \rightarrow V_2\)의 표현행렬이 \(M(T)\)이면, 기저 \(B_2 ^*,\) \(B_1 ^*\)에 대한 전치함수 \(T^* : V_2^* \rightarrow V_1^*\)의 표현행렬은 다음과 같다. \[M(T^*) = \, ^t \! M(T).\] 즉 선형변환 \(T\)의 전치함수의 표현행렬은 \(T\)의 표현행렬의 전치행렬과 같다.
증명.
기저 \(B_2 ^*,\) \(B_1 ^*\)에 대한 \(T^*\)의 표현행렬의 \(j\)째 열벡터는 \(v_1^*,\) \(\cdots,\) \(v_n^*\)에 대한 \(T^*(w_j ^*)\)의 좌표벡터와 같다. 이것은 다음 세 가지 사실을 염두에 두면 쉽게 계산된다.
- 선형변환 \(f:V\rightarrow K\)는 쌍대기저의 일차결합으로 다음과 같이 표현된다.\[f = \sum_{j=1}^n f(v_j)v_j^*\]
- 기저 \(B_1,\) \(B_2\)에 대하여 \(M(T) = (a_{ij})\)이면\[T(v_j) = \sum_{i=1}^m a_{ij}w_i\]이다. 왜냐하면 \(M(T)\)의 \(j\)째 열벡터는 \(T(v_j)\)를 \(w_1,\) \(\cdots,\) \(w_m\)의 일차결합으로 표현하기 위한 계수이기 때문이다.
- 쌍대기저의 정의에 의하여\[w_j^* \left( \sum_{i=1}^m \lambda_i w_i \right) = \lambda_j\]이다. 왜냐하면 \(w_j^*\)는 \(w_j\)를 제외한 다른 기저원소를 \(0\)에 대응시키기 때문이다.
이와 같은 성질을 이용하여 \(T^* (w_j^*)\)를 계산하면 다음과 같다. \[\begin{align} T^*(w_j^*) &= w_j^* \circ T = \sum _{i=1}^n [ w_j^* \circ T](v_i)v_i^* \\[5pt] &=\sum_{i=1}^n w_j^* (T(v_i ))v_i^* = \sum _{i=1}^n w_j^* \left( \sum_{k=1}^m a_{ki} w_k \right) v_i^*\\[5pt] &= \sum_{i=1}^n a_{ji} v_i^*. \end{align}\] 이로써 \(M(T^*)\)의 \(j\)째 열벡터와 \(M(T)\)의 \(j\)째 행벡터가 일치하므로 \(M(T^*) = \,^t \! M(T)\)이다.
이로써 행렬의 행벡터가 가지는 성질과 열벡터가 가지는 성질을 서로 교환할 수 있다.
따름정리 7. 행렬의 행공간의 차원과 열공간의 차원은 같다.
더욱이 연립일차방정식과 관련하여 다음 결과를 얻는다.
따름정리 8. \(A\in M_n (K)\)라고 하자. 이때 다음은 모두 서로 동치이다.
- 임의의 \(\mathbf{y}\in K^n\)에 대하여 연립일차방정식 \(A\mathbf{x} = \mathbf{y}\)는 적어도 하나의 해를 가진다.
- \(A\)의 열벡터들은 \(K^n\)을 생성한다.
- \(A\)의 행벡터들은 \(K^n\)을 생성한다.
- 동차방정식 \(A\mathbf{x} = \mathbf{0}\)은 자명한 해 \(\mathbf{x} = \mathbf{0}\)만을 가진다.
- \(A\)의 열벡터들은 일차독립이다.
- \(A\)의 행벡터들은 일차독립이다.
- 임의의 \(\mathbf{y}\in K^n\)에 대하여 연립일차방정식 \(A\mathbf{x} = \mathbf{y}\)는 딱 하나의 해를 가진다.
- \(A\)의 열벡터들은 \(K^n\)의 기저를 이룬다.
- \(A\)의 행벡터들은 \(K^n\)의 기저를 이룬다.
- \(A\)는 가역이다. 즉 \(A\in\operatorname{GL}_n (K)\)이다.
이중쌍대공간
\(V\)가 벡터공간일 때 \(V\)의 쌍대공간의 쌍대공간을 \(V\)의 이중쌍대공간(double dual space)이라고 부르고 \(V^{**}\)로 나타낸다.
\(V\)와 \(V^*\)가 동형임을 보일 때 \(V\)의 기저를 이용하여 쌍대기저를 구성한 뒤, 그것이 \(V^*\)의 기저가 됨을 보였다. 그러나 \(V\)와 \(V^{**}\)이 동형임을 보일 땐 \(V\)의 기저와 상관 없이 두 공간 사이의 동형사상을 구성할 수 있다.
\(v\in V\)가 주어졌다고 하자. 이때 임의의 \(f\in V^*\)를 \(f(v)\)에 대응시키는 함수 \(e_v : V^* \rightarrow K\)를 생각하자. 즉 \(e_v (f) = f(v)\)이다. 이 함수는 \(V^*\)로부터 \(K\)로의 선형변환이 된다. 즉 \(e_v \in V^{**}\)이다. 만약 \[v \mapsto e_v\] 로서 \(V\)의 원소를 \(V^{**}\)에 대응시키면, 이러한 대응은 두 공간 사이의 선형변환이면서 일대일 대응이 된다. 이렇게 두 공간 사이의 동형사상이 기저와 무관하게 정해지는데, 이러한 관점에서 ‘\(V\)와 \(V^{**}\)는 표준적으로 동형이다(canonically isomorphic)’라고 말한다.
기저의 변환
벡터공간의 기저가 어느것이 주어졌느냐에 따라서 그 벡터공간 위에서 정의된 선형변환의 표현행렬이 달라진다. 벡터공간의 기저가 다른 것으로 바뀌었을 때 선형변환의 표현행렬이 어떻게 달라지는지 살펴보자.
\(B = \left\{v_1 ,\, \cdots ,\, v_n\right\}\)과 \(B ' = \left\{ w_1 ,\, \cdots ,\, w_n \right\}\)이 벡터공간 \(V\)의 기저라고 하자. 그러면 좌표함수 \(\gamma_B\)와 \(\gamma_{B ' }\)은 모두 \(V\)로부터 \(K^n\)으로의 동형사상이다. 이때 \(P = \gamma_B \circ \gamma_{B '} ^{-1}\)라고 하면 \(P\)는 \(K^n\)으로부터 \(K^n\)으로의 동형사상이다. 더욱이 \(P\)는 기저 \(B ' \)에 의하여 표현된 \(V\)의 벡터를 기저 \(B\)에 의하여 표현된 \(V\)의 동일한 벡터에 대응시키는 함수이다. 이와 같이 정의된 함수 \(P\)를 \(B ' \)로부터 \(B\)로의 기저변환행렬이라고 부른다. 기저변환행렬과 기저변환행렬이 나타내는 함수를 구분하기 위하여, 이와 같이 정의된 함수를 \(T_P\)로 나타내고 그 행렬을 \(P\)로 나타내기도 한다.
각 \(j = 1,\,\cdots,\,n\)에 대하여 \[P\gamma_{B'} (w_j) = \gamma_B (w_j)\] 이다. 이 등식의 좌변은 \(P\mathbf{e}_j = P^j\)이고 우변은 \(w_j\)의 기저 \(B\)에 대한 좌표이다. 그러므로 기저변환행렬 \(P\)는 다음과 같은 방법으로 구할 수 있다.
기저변환행렬 \(P\)의 \(j\)째 열은 \(w_j\)의 기저 \(B\)에 대한 좌표벡터이다.
보기 4. \(V\)가 차수가 2 이하인 실계수 다항함수들의 모임이라고 하자. 그리고 \(V\)의 두 기저 \[B = \left\{ 1,\,x,\,x^2 \right\} ,\,\, B ' = \left\{ 1+x ,\, 1-x ,\, 1+x^2 \right\}\] 을 생각하자. 이때 \(B ' \)으로부터 \(B\)로의 기저변환행렬은 다음과 같다. \[P = \left(\begin{array}{crc} 1 & 1 & 1 \\ 1 & -1 & 0 \\ 0 & 0 & 1 \end{array}\right).\]
정리 9. \(V\)가 유한차원 벡터공간이고 \(T:V\rightarrow V\)가 선형변환이라고 하자. 그리고 \(B\)와 \(B ' \)이 \(V\)의 기저이며 \(P\)가 \(B ' \)으로부터 \(B\)로의 기저변환행렬이라고 하자. 만약 기저 \(B\)에 대한 \(T\)의 표현행렬이 \(M\)이고, 기저 \(B ' \)에 대한 \(T\)의 표현행렬이 \(N\)이면, 다음이 성립한다. \[N = P^{-1} MP.\]
증명.
화끈하게 다이어그램 한 장으로 증명을 마친다.
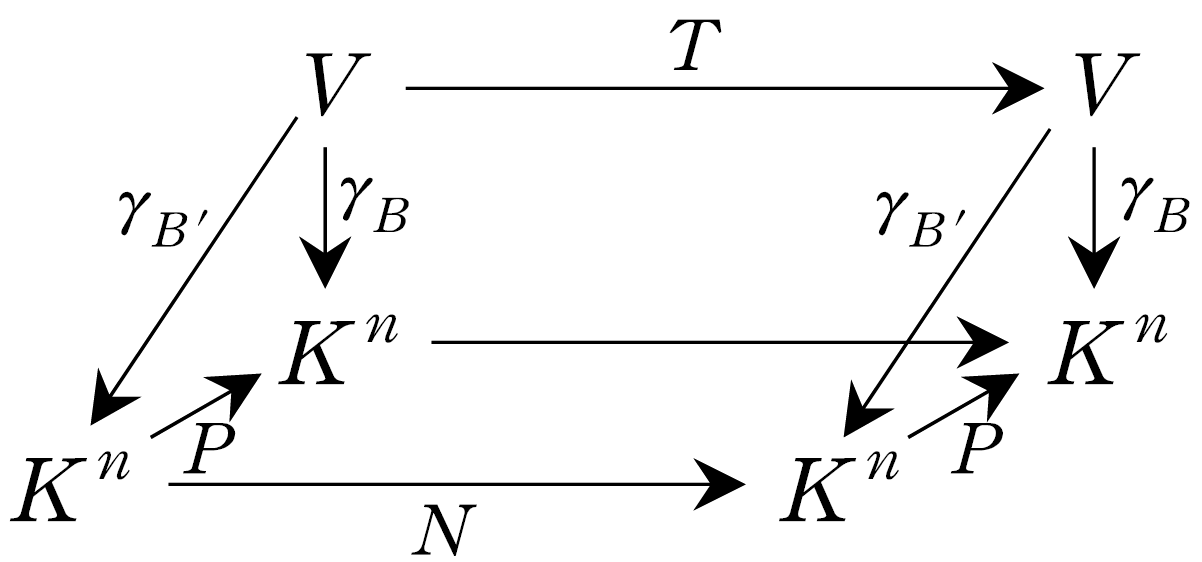(써 놓고 보니 \(K^n\)과 \(K^n\) 사이에 \(M\)이 빠졌네.)
보기 5. 보기 4의 내용을 이어서 살펴보자. 기저를 \(B\)에서 \(B ' \)으로 바꾸었을 때 미분연산자의 표현행렬을 구해 보자. 먼저 기저변환행렬의 역행렬을 구하면 다음과 같다. \[P^{-1} = \left(\begin{array}{crr} 1/2 & 1/2 & -1/2 \\ 1/2 & -1/2 & -1/2 \\ 0 & 0 & 1 \end{array}\right).\] 그러므로 기저 \(B ' \)에 대한 미분연산자 \(D\)의 표현행렬은 다음과 같다. \[P^{-1}DP = \left(\begin{array}{crr} 1/2 & 1/2 & -1/2 \\ 1/2 & -1/2 & -1/2 \\ 0 & 0 & 1 \end{array}\right) \left(\begin{array}{ccc} 0 & 1 & 0 \\ 0 & 0 & 2 \\ 0 & 0 & 0 \end{array}\right) \left(\begin{array}{crc} 1 & 1 & 1\\ 1 & -1 & 0 \\ 0 & 0 & 1 \end{array}\right). \] 이것을 계산하면 다음을 얻는다. \[P^{-1}DP = \left(\begin{array}{crr} 1/2 & -1/2 & 1 \\ 1/2 & -1/2 & -1 \\ 0 & 0 & 0 \end{array}\right). \]
두 행렬 \(A,\,B \in M_n (K)\)이 주어졌다고 하자. 만약 가역행렬 \(P\in\operatorname{GL}_n (K)\)가 존재하여 \(B = P^{-1}AP\)를 만족시키면, 두 행렬을 서로 닮은행렬(similar)이라고 부르고, \(A \sim B\)로 나타낸다.
행렬의 닮음 관계는 동치관계이다. 즉 행렬의 닮음 관계는 반사적이고 반대칭적이며 추이적이다. 더욱이 다음이 성립한다.
정리 10. 두 행렬 \(M,\,M ' \in M_n (K)\)가 서로 닮음일 필요충분조건은 \(n\)차원 벡터공간 \(V\)와 선형변환 \(T\), 그리고 두 기저 \(B,\) \(B ' \)이 존재하여 \(T\)의 \(B ,\) \(B ' \)에 대한 표현행렬이 \(M,\) \(M ' \)이 되는 것이다.
증명.
\(M ' = P^{-1}MP\)라고 가정하자. 그리고 \(V=K^n\)이라고 하자. 그러면 \(M\)은 표준기저에 대한 \(T_M\)의 표현행렬이다. 이제 \(P\)의 열벡터로 이루어진 기저원소 \(P^1 ,\) \(\cdots ,\) \(P^n\)을 생각하자. 이 기저로부터 표준기저로의 기저변환행렬은 \(P\)이다. 그러므로 기저원소 \(P^j\)에 대한 \(T_M\)의 표현행렬은 \(M ' =P^{-1}MP\)와 같다.
역이 성립한다는 사실은 정리 9로부터 얻는다.