Exercises: Representation of Linear Transformations

Solution. Suppose \((x_1 ,\,x_2 )\) be given. Take \(\lambda_1 = x_1 ,\) \(\lambda_2 = x_2 - x_1 ,\) then \[(x_1 ,\,x_2 ) = \lambda_1 (1,\,1) + \lambda_2 (0,\,1).\] Therefore, we have \[\begin{align} T(x_1 ,\,x_2 ) &= x_1 T((1,\,1)) + (x_2 - x_1 ) T((0,\,1)) \\[5pt] &= x_1 \times 5 + (x_2 - x_1 ) \times 2 \\[5pt] &= 3x_1 + 2x_2 . \end{align}\]

Solution. \[ [T] = [T(e_1) \quad T(e_2) \quad T(e_3)] = \left[ \begin{array}{crr} 5 & -2 & 1\\ 0 & 4 & -7 \end{array} \right] \]

Solution. The formula for \(T\) is \[T((x,\,y)) = (y,\,x).\] Hence the matrix of \(T\) is \[[T] = [ T((1,\,0)) \quad T((0,\,1))] = \left[ \begin{array}{cc} 0 & 1 \\ 1 & 0 \end{array} \right].\] Since an iterated reflection(twice) through a fixed line does not change anything, \(T\circ T\) is the identity function.

Solution. Since \[[D(e^x )] = [e^x] = (1,\,0)\] and \[[D(e^{2x})] = [2e^{2x}] = (0,\,2),\] we have \[[D] = \left[\begin{array}{cc} 1 & 0 \\ 0 & 2 \end{array}\right].\] As an example, let \[f(x) = 3e^x + 4e^{2x}.\] Then \[[f] = (3,\,4).\] and \[[D][f] = \left[\begin{array}{cc} 1 & 0 \\ 0 & 2 \end{array}\right]\left[\begin{array}{c} 3 \\ 4 \end{array}\right] = \left[\begin{array}{c} 3 \\ 8 \end{array}\right].\] Furthermore, since \[Df(x) = f ' (x) = 3e^x + 8e^{2x},\] we have \[[Df] = \left[\begin{array}{c} 3 \\ 8 \end{array}\right].\] Therefore \([Df] = [D][f].\)

Solution. The matrix representation for \(\rho_j\) is \([a_{1k}]\) where \(a_{1k} = 1\) for \(k=j\) and \(a_{1k} = 0\) otherwise. For example, if \(n=4\) and \(j=2,\) the matrix repersentation for \(\rho_2\) is \[\left[\begin{array}{cccc} 0 & 1 & 0 & 0 \end{array}\right].\]

Solution. Let \[\begin{align} v_1 & : x \mapsto \sin x ,\\[5pt] v_2 & : x \mapsto \sin 2x , \\[5pt] v_3 & : x \mapsto e^x , \end{align}\] then \[\begin{align} (D^2 v_1) (x) &= -\sin x = -v_1, \\[5pt] (D^2 v_2) (x) &= -4 \sin 2x = -4v_2 ,\\[5pt] (D^2 v_3) (x) &= e^x = v_3 , \end{align}\] that is, \[\begin{align} [D^2 ] \left[\begin{array}{c} 1 \\ 0 \\ 0 \end{array}\right] &= \left[\begin{array}{r} -1 \\ 0 \\ 0 \end{array}\right], \\[4pt] [D^2 ] \left[\begin{array}{c} 0 \\ 1 \\ 0 \end{array}\right] &= \left[\begin{array}{r} 0 \\ -4 \\ 0 \end{array}\right], \\[4pt] [D^2 ] \left[\begin{array}{c} 0 \\ 0 \\ 1 \end{array}\right] &= \left[\begin{array}{r} 0 \\ 0 \\ 1 \end{array}\right]. \end{align}\] Hence \[[D^2] = \left[\begin{array}{rrc} -1 & 0 & 0 \\ 0 & -4 & 0 \\ 0 & 0 & 1 \end{array}\right].\]

Solution. Since \(I(e_j) = e_j,\) we have \([I] = [e_1 \,\,\, e_2 \,\,\, \cdots \,\,\, e_n] = I_n.\)

Solution. Suppose that \(T\) is invertible, then \(T^{-1}: V ' \rightarrow V\) exists. Furthermore, since \(T\) is one-to-one correspondence, \(V\) and \(V'\) are isomorphic and have the same dimension. Observe that \[[T]_{B,B '} [T^{-1}]_{B',B} = [T\circ T^{-1}]_{B',B'} = [I_{V'}]_{B'} = I\] and \[ [T^{-1}]_{B',B}[T]_{B,B '} = [T^{-1} \circ T]_{B,B} = [I_{V}]_{B} = I ;\] Thus \([T^{-1}]_{B',B}\) is the inverse matrix for \([T]_{B,B'}.\)

To prove the converse, suppose that \([T]_{B,B'}\) is invertible, then the inverse matrix \(([T]_{B,B'})^{-1}\) exists. Define the linear transformation \(U : V ' \rightarrow V\) by \[U : [v']_{B'} \mapsto ([T]_{B,B'})^{-1}[v']_{B'}\] for \(v' \in V'.\) Then, for each \(v' \in V',\) there exists \(v\in V\) such that \[[v]_{B} = ( [T]_{B,B'})^{-1} [v']_{B'}.\] Hence we have \[\begin{align} [(T\circ U)(v')]_{B'} &= [T]_{B,B'} [U]_{B',B} [v']_{B'} \\[5pt] &= [T]_{B,B'} ([T]_{B,B'})^{-1} [v']_{B'} \\[5pt] &= [I]_{B'} [v']_{B'} = [v']_{B'} \end{align}\] and \[\begin{align} [(U\circ T)(v)]_{B} &= [U]_{B',B} [T]_{B,B'} [v]_{B} \\[5pt] &= ([T]_{B,B'})^{-1} [T]_{B,B'} [v]_{B} \\[5pt] &= [I]_{B} [v]_{B} = [v]_{B}, \end{align}\] that is, both \(T\circ U\) and \(U\circ T\) are identity functions. Therefore \(U\) is the inverse function for \(T\) and we conclude that \(T\) is invertible.

Solution. \([T_\lambda ] = \lambda I_n .\)

Solution. Since \[[2+5x-4x^2]_B = \left[\begin{array}{r} 2 \\ 5 \\ -4 \end{array}\right],\] we have \[\begin{align} [T(2+5x-4x^2 )]_B &= \left[\begin{array}{ccc} 2 & 0 & 1 \\ 0 & 1 & 2 \\ 1 & 1 & 1 \end{array}\right] \left[\begin{array}{r} 2 \\ 5 \\ -4 \end{array}\right] \\[4pt] &= \left[\begin{array}{r} 0 \\ -3 \\ 3 \end{array}\right] = [0 - 3x + 3x^2 ]_B . \end{align}\] Therefore \(T(2+5x-4x^2) = -3x+3x^2 .\)

Solution. Since \[\begin{align} D(1) & = 2 , \\[5pt] D(x) &= 1+2x ,\\[5pt] D(x^2) &= -10 + 2x +2x^2 , \end{align}\] we have \[[D] = \left[\begin{array}{ccr} 2 & 1 & -10 \\ 0 & 2 & 2 \\ 0 & 0 & 2 \end{array}\right].\] Since \([D]\) is invertible, \(D\) is invertible.

Another way to show the invertibility of \(D\) is as follows: It is easily shown that \(p(x)=0\) only for \(x=0,\) that is, \(\operatorname{Ker}(D) = \left\{0\right\}.\) Hence \(D\) is one-to-one correspondence and \(D\) is invertible.

Solution. (1) Since \[\begin{align} (a+bi)(1+0i) &= a+bi ,\\[5pt] (a+bi)(0+1i) &= -b+ai , \end{align}\] we have \[[T_z] = \left[\begin{array}{cr} a & -b \\ b & a \end{array}\right].\] (2) \[[T_z]^{-1} = \frac{1}{a^2 + b^2} \left[\begin{array}{rc} a & b \\ -b & a \end{array}\right] = [T_{1/z}].\] (3) \[\left[\begin{array}{cr} 0 & -1 \\ 1 & 0 \end{array}\right].\] (4) \[\begin{align} A^{1000} &= [T_i]^{1000} = [T_{i^{1000}}] = [T_1] = \left[\begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array}\right],\\[4pt] A^{1003} &= [T_i]^{1003} = [T_{i^{1003}}] = [T_{-i}] = \left[\begin{array}{cc} 0 & 1 \\ -1 & 0 \end{array}\right]. \end{align}\]

Solution. Since \[ \left[\begin{array}{ccc} 2 & 0 & 1 \\ 1 & 1 & 5 \\ 2 & 1 & 2 \end{array}\right] \left[\begin{array}{r} 2 \\ -1 \\ 5 \end{array}\right] = \left[\begin{array}{r} 9 \\ 26 \\ 13 \end{array}\right], \] we have \(T(2v_1 - v_2 + 5v_3 ) = 9 v_1 + 26 v_2 + 13 v_3 .\)

Solution. If \(n=0,\) then there's nothing to prove; Hence assume that \(n > 0.\)

Let \(\dim(V)=m \ge n.\) If \(m=n,\) then \(T\) is the zero map and there's no need to prove. Hence suppose that \(m > n.\) Since \(\dim(\operatorname{Ker}(T))=n,\) we can take a basis for \(\operatorname{Ker}(T)\) that consists of \(n\) vectors, say \(v_1 ,\) \(v_2 ,\) \(\cdots,\) \(v_n.\) Expand this collection to the basis for \(V,\) say \[v_1 ,\, v_2 ,\, \cdots ,\, v_n ,\, \cdots ,\, v_m .\] By construction, \(v_{n+1},\) \(\cdots,\) \(v_m\) don't belong to the kernel of \(T.\) With this collection, we have \[T(v_1 ) =0 ,\, T(v_2) =0 ,\, \cdots ,\, T(v_n) =0\] and \[T(v_{n+1}) \ne 0 ,\, \cdots ,\, T(v_m) \ne 0.\] Hence this collection constitutes a desired basis.

Solution. If \(r=0\) or \(r=1,\) then the result obviously follows. If \(r\ge 2,\) then \[[T^r] = [T]^r = A^r.\] The result directly comes from this identity.

Solution. Take a basis for \(W\) consisting of \(m\) vectors, say \[v_1 ,\, v_2 ,\, \cdots ,\, v_m .\] Expand this collection to the basis for \(V,\) say \[v_1 ,\, v_2 ,\, \cdots ,\, v_m ,\, v_{m+1} ,\, \cdots ,\, v_n.\tag{*}\] By construction, \(v_{m+1},\) \(\cdots,\) \(v_n\) don't belong to \(W.\) Furthermore \(T(v_j)\in W\) for \(j \le m.\) Hence, if \(j \le m,\) \(T(v_j)\) is expressed by a linear combination of \(v_1 ,\) \(\cdots ,\) \(v_m,\) say \[T(v_j) = \lambda_{j1} v_1 + \lambda_{j2} v_2 +\cdots + \lambda_{jm} v_m + 0v_{m+1} + \cdots + 0v_n .\] Hence the collection (*) constitutes a desired basis.

Solution. The solution is not that far from the solutions of problems 14 and 16. Take a basis \[v_1 ,\, v_2 ,\, \cdots ,\, v_{n_1} ,\, w_1 ,\, w_2 ,\, \cdots ,\, w_{n_2}\] where all \(v_i ' \text{s}\) belong to \(W_1\) and all \(w_j ' \text{s}\) belong to \(W_2 .\)

Solution. Take \[A = [T] = [a_{ij}]_{n\times n}\] where \[a_{ij} = \begin{cases} 1 \quad & \text{if} \, i \equiv j+1 \, (\text{mod} \, n) \\ 0 \quad & \text{otherwise.} \end{cases}\] If \(k\) is a positive integer less than or equal to \(n,\) then \[A^k = [T]^k = [b_{ij}]_{n\times n}\] where \[b_{ij} = \begin{cases} 1 \quad & \text{if} \, i \equiv j+k \, (\text{mod} \, n) \\ 0 \quad & \text{otherwise.} \end{cases}\] If \(k=n,\) we have \(A^n = I_n ,\) the identity matrix.

As an example, if \(n=5,\) then \[A=[T] = \left[\begin{array}{ccccc} 0 & 0 & 0 & 0 & 1 \\ 1 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 \end{array}\right]\] and \[A^2 =[T]^2 = \left[\begin{array}{ccccc} 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 1 \\ 1 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 \end{array}\right].\]

Solution. Take \[\begin{align} v_1&\in W_1 , \\[5pt] v_2&\in W_2 \setminus W_1 , \\[5pt] v_3&\in W_3 \setminus W_2 , \\[5pt] &\vdots \\[5pt] v_n&\in W_n \setminus W_{n-1}. \end{align}\] inductively. Then \(T(v_j)\) is expressible by a linear combination of the first \(j\) vectors of this collection.

Solution. Let \(S\) be the canonical basis. \[P_{B\rightarrow S} = \left[\begin{array}{rcr} 1 & 6 & -1 \\ 2 & 0 & 2 \\ -1 & 1 & 2 \end{array}\right].\]

Solution. Observe \[\begin{align} v_1 &= (1+x)^0 = 1 , \\[5pt] v_2 &= (1+x)^1 = 1+x , \\[5pt] v_3 &= (1+x)^2 = 1 + 2x + x^2 , \\[5pt] v_4 &= (1+x)^3 = 1 + 3x + 3x^2 + x^3 , \\[5pt] v_5 &= (1+x)^4 = 1 + 4x + 6x^2 + 4x^3 + x^4 . \end{align}\] Hence \[P_{B ' \rightarrow B} = \left[\begin{array}{ccccc} 1 & 1 & 1 & 1 & 1 \\ 0 & 1 & 2 & 3 & 4 \\ 0 & 0 & 1 & 3 & 6 \\ 0 & 0 & 0 & 1 & 4 \\ 0 & 0 & 0 & 0 & 1 \end{array}\right].\] To find the inverse transition matrix, we see that \[\begin{align} 1 & = v_1 ,\\[5pt] x &= -v_1 + v_2 ,\\[5pt] x^2 &= v_1 - 2v_2 + v_3 , \\[5pt] x^3 &= -v_1 + 3v_2 - 3v_3 + v_4 , \\[5pt] x^4 &= v_1 - 4v_2 + 6v_3 - 4v_4 + v_5 . \end{align}\] Hence \[P_{B \rightarrow B ' } = \left[\begin{array}{rrrrr} 1 & -1 & 1 & -1 & 1 \\ 0 & 1 & -2 & 3 & -4 \\ 0 & 0 & 1 & -3 & 6 \\ 0 & 0 & 0 & 1 & -4 \\ 0 & 0 & 0 & 0 & 1 \end{array}\right].\] Obviously, \(P_{B \rightarrow B ' }\) is the inverse matrix of \(P_{B ' \rightarrow B}.\)

Solution. Let \(v\in V\) be given. Since \[Q[v]_{B ' ' } = [v]_{B '}\] and \[P[v]_{B'} = [v]_{B},\] we have \[(PQ)[v]_{B''} = P(Q[v]_{B''}) = P[v]_{B'}= [v]_B.\] Hence the transition matrix from \(B''\) to \(B\) is \(PQ.\)

Solution. Let \(M_1\) and \(M_2\) be similar matrices. Then there exist a vector space \(V,\) bases \(B_1 ,\) \(B_2 \) for \(V,\) and a linear transformation \(T : V \rightarrow V\) such that \[ [T]_{B_1} = M_1 \quad \text{and} \quad [T]_{B_2} = M_2 .\] Hence \[\operatorname{rank}(M_1) = \dim(\operatorname{Im}(T)) = \operatorname{rank}(M_2 ).\] (You have to fill the descriptions.)

Solution. Suppose that \(A = [T]_B ,\) then \(T_A = T.\) Hence \(A \mapsto T_A\) is the inverse map. (You need to show that this mapping is well-defined.)

Solution. The given datum are translated as follows:

(1) \([T]_{B,C} = M;\)
(2) \([T]_{B',C'} = N;\)
(3) \(P_{B'\rightarrow B}=P ,\,\, P_{C'\rightarrow C} = Q.\)

This translation can be expressed by the diagram as follows:

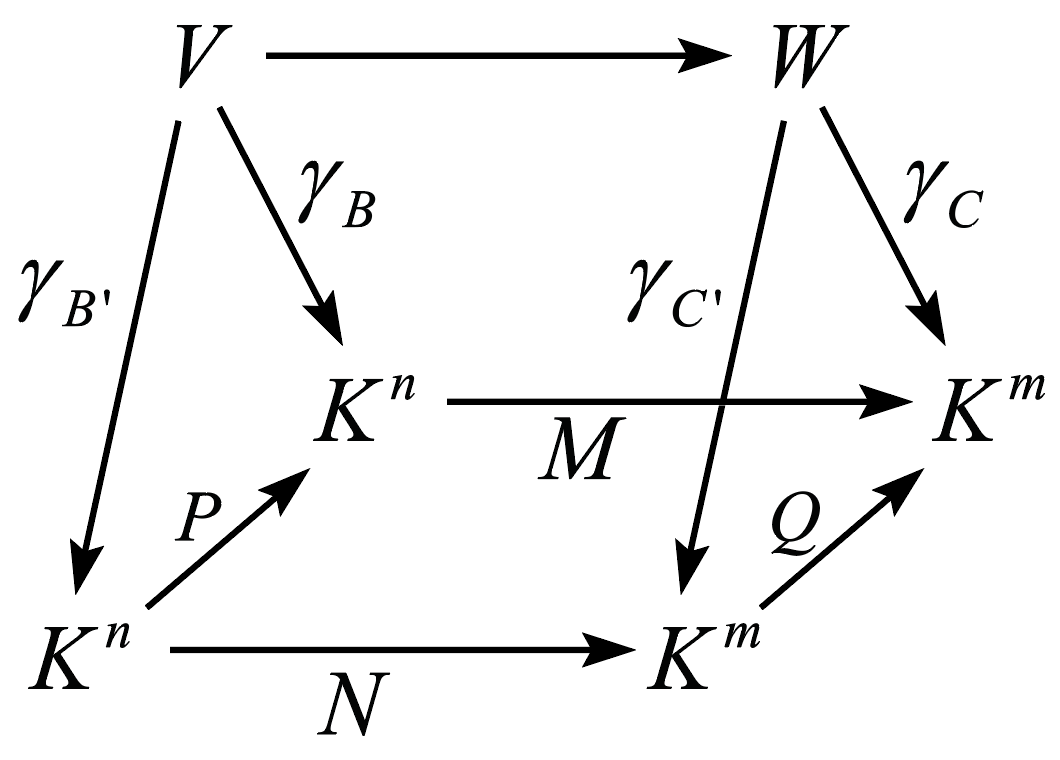
Hence \(M = QNP^{-1}\) and \(N = Q^{-1} MP.\)

Solution. Since \[(T_A \circ T_B)^* = T_B ^* \circ T_A^*,\] we have \[(AB)^T = [ (T_A \circ T_B)^* ] = [T_B ^*][T_A ^*] = B^T A^T .\]