사면체의 겉넓이가 최소가 되도록 하는 꼭짓점의 위치

풀이. 점 \(\mathrm{Q}\)가 삼각형 \(\mathrm{ABC}\)의 내부에 있는 경우를 생각하자. 그리고 점 \(\mathrm{Q}\)로부터 세 변 \(\mathrm{BC},\) \(\mathrm{CA},\) \(\mathrm{AB}\)까지의 거리를 각각 \(x,\) \(y,\) \(z\)라고 하자. 만약 점 \(\mathrm{Q}\)가 삼각형 \(\mathrm{ABC}\)의 내부에 있지 않다면 \(x,\) \(y,\) \(z\) 중 하나 이상의 값을 \(0\) 이하가 되도록 함으로써 점 \(\mathrm{Q}\)의 위치를 \(x,\) \(y,\) \(z\)에 대응시킬 수 있다.

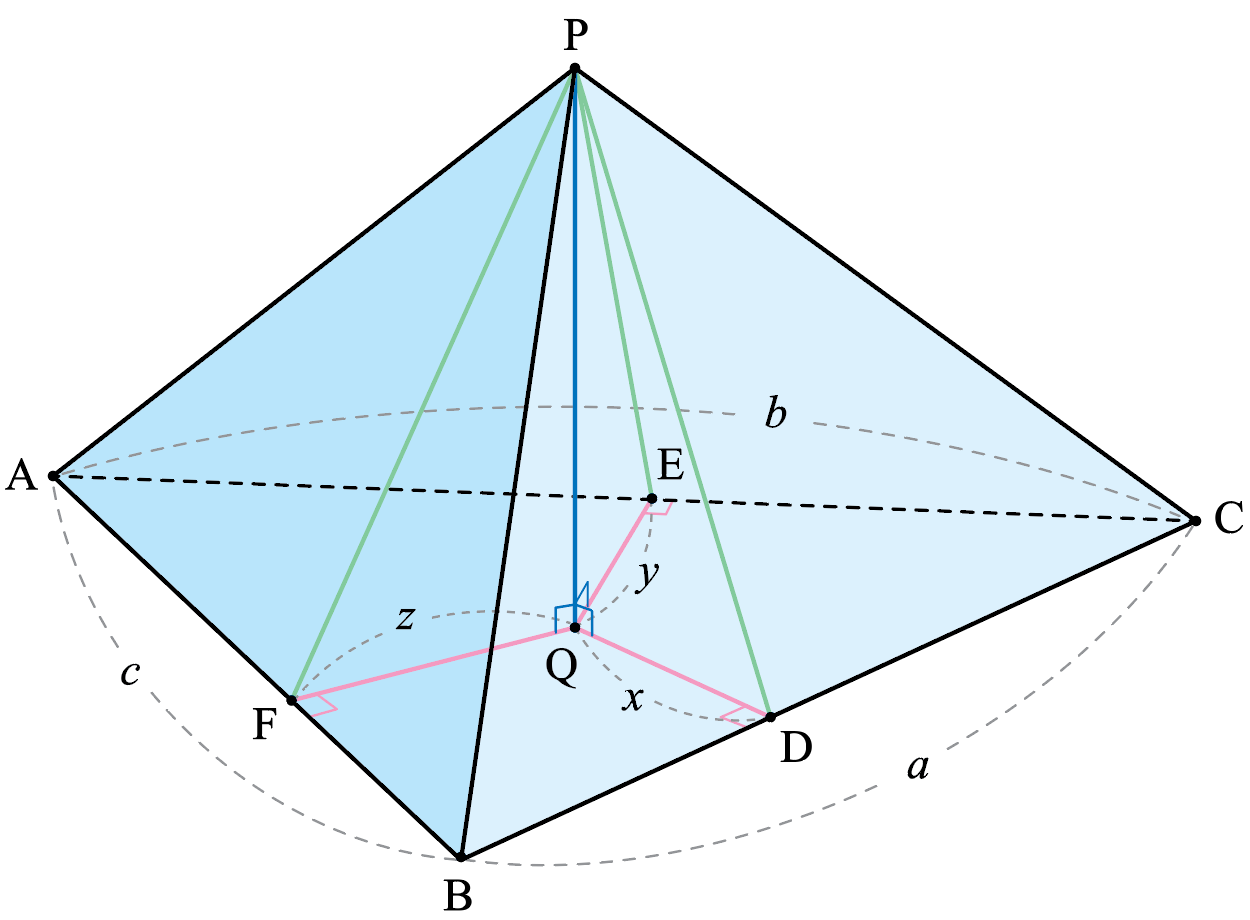
또한 세 변 \(\mathrm{BC},\) \(\mathrm{CA},\) \(\mathrm{AB}\)의 길이를 각각 \(a,\) \(b,\) \(c\)라고 하고, 사면체의 높이인 선분 \(\mathrm{PQ}\)의 길이를 \(h\)라고 하자.

삼각형 \(\mathrm{ABC}\)의 넓이를 \(S\)라고 하면 \[\frac{1}{2} (ax+ by + cz) = S\] 이고, 사면체의 부피는 \[\frac{1}{3} Sh = \frac{1}{6} (ax+by+cz)h = \text{(constant)}\] 이다. 사면체의 부피와 밑면의 넓이가 일정하므로 사면체의 높이 \(h\) 또한 상수이다. 그러므로 점 \(\mathrm{P}\)의 위치는 점 \(\mathrm{Q}\)의 위치에 의하여 완전히 결정된다.

한편 사면체의 겉넓이는 밑면의 넓이와 옆면의 넓이를 더하면 되는데 밑면의 넓이가 상수이므로, 우리가 원하는 결과를 얻기 위해서는 옆면의 넓이가 최소가 되도록 하면 된다. \[\begin{gather} \overline{\mathrm{PD}} = \sqrt{x^2 + h^2} , \\[6pt] \overline{\mathrm{PE}} = \sqrt{y^2 + h^2} , \\[6pt] \overline{\mathrm{PF}} = \sqrt{z^2 + h^2} \end{gather}\] 이므로, 사면체의 옆면의 넓이는 \[\frac{1}{2} \left( a\sqrt{x^2 + h^2} + b\sqrt{y^2 + h^2} + c\sqrt{z^2 + h^2} \right)\] 이다.

함수 \(f\)와 \(g\)를 다음과 같이 정의하자. \[\begin{gather} f(x,\,y,\,z) = a\sqrt{x^2 + h^2} + b\sqrt{y^2 + h^2} + c\sqrt{z^2 + h^2} ,\\[6pt] g(x,\,y,\,z) = ax+by+cz. \end{gather}\] 이제 우리는 제한조건 \[g(x,\,y,\,z) = \text{(constant)}\] 아래에서 함수 \(f(z,\,y,\,z)\)가 최솟값을 갖도록 하는 점 \((x,\,y,\,z)\)를 구해야 한다. 라그랑주의 방법을 이용하자. 그러한 점 \((x,\,y,\,z)\)가 존재한다면 상수 \(\lambda\)가 존재하여 다음 등식을 만족시켜야 한다. \[\begin{gather} \nabla f(x,\,y,\,z) = \lambda \nabla g(x,\,y,\,z) \end{gather}\] 이 식을 풀어 쓰면 다음과 같다. \[ \frac{ax}{\sqrt{x^2 + h^2}} \textbf{i} + \frac{by}{\sqrt{y^2 + h^2}} \textbf{j} + \frac{cz}{\sqrt{z^2 + h^2}} \textbf{k} = \lambda \left( a\textbf{i} + b\textbf{j}+ c \textbf{k} \right)\] 이 등식이 성립하려면 \[\frac{x}{\sqrt{x^2 + h^2}} = \frac{y}{\sqrt{y^2 + h^2}} = \frac{z}{\sqrt{z^2 + h^2}} \] 이어야 하고, 이것을 풀면 \[x = y = z\] 이다. 즉 점 \(\mathrm{Q}\)가 삼각형 \(\mathrm{ABC}\)의 내심일 때 사면체의 겉넓이는 극값을 가진다.

이제 \(x = y = z\)인 점 \((x,\,y,\,z)\)에서 \(f\)가 최솟값을 가짐을 보이자. 일단 라그랑주의 방법을 통해서 발견된 점은 \(x=y=z\)인 점 \((x,\,y,\,z)\) 뿐이므로, 다른 점에서는 \(f\)가 극값을 갖지 않는다. 그러므로 \((x,\,y,\,z)\)가 \((0,\,0,\,0)\)으로부터 무한히 멀어지는 경우를 조사하면 된다.

점 \((x,\,y,\,z)\)가 \((0,\,0,\,0)\)으로부터 무한히 멀어지는 것은 점 \(\mathrm{Q}\)가 \((0,\,0)\)으로부터 무한히 멀어지는 것과 같다. 그런데 점 \(\mathrm{Q}\)가 \((0,\,0)\)으로부터 무한히 멀어지면 사면체의 옆면을 이루는 세 삼각형 중 하나 이상의 높이가 무한히 길어지므로, 사면체의 겉넓이 또한 무한히 커진다. 그러므로 \(f\)는 \(x=y=z\)인 점 \((x,\,y,\,z)\)에서의 함숫값보다 더 작은 함숫값을 가질 수 없다.