이 포스트에서는 모멘트와 질량중심을 수학적으로 정의하고, 질량중심을 계산하는 공식을 살펴본다. 더불어 질량중심을 이용하여 회전체의 부피와 넓이를 쉽게 계산할 수 있는 파푸스의 정리를 살펴본다.
모멘트와 질량중심의 정의
모멘트와 질량중심은 세 단계로 정의한다. 먼저 직선 위에 놓인 유한 개의 물체에 대하여 정의하고, 다음으로 평면에 놓인 유한 개의 물체에 대하여 정의한 뒤, 마지막으로 평면에 놓인 물체(각 좌표에서 밀도가 함수로 주어진)에 대하여 정의한다.
(1) 직선 위에 놓인 유한 개의 물체
아래 그림처럼 수직선 위에 세 물체가 놓여 있다. 각 물체의 위치는 \(x_k\)이고 질량은 \(m_k\)이다. 그리고 원점에는 받침대가 놓여 있다. (물체의 크기가 무척 작아서 물체의 위치가 한 점으로 표현될 수 있는 이상적인 상황을 가정하자.)

원점을 기준으로 했을 때 각 물체가 지렛대에 미치는 토크, 즉 지렛대를 회전하게 만드는 힘은 \(g x_k m_k \)이다. 여기서 \(g\)는 상수이다. 이때 계(system; 물체 전체)가 지렛대를 회전하게 만드는 힘은 \[g x_1 m_1 + gx_2 m_2 + gx_3 m_3 = g(x_1 m_1 + x_2 m_2 + x_3 m_3 )\] 이다. 여기서 \((x_1 m_1 + x_2 m_2 + x_3 m_3 )\)을 원점에 대한 계의 모멘트(moment of the system about the origin)라고 부른다. 이 값이 양수이면 지렛대의 오른쪽 부분이 내려가고, 이 값이 음수이면 지렛대의 왼쪽 부분이 내려간다.
지렛대가 어느 부분도 내려가지 않고 수평하게 유지되려면 받침대를 어느 위치에 놓아야 할까? 아래 그림에서처럼 그 위치를 \(\overline{x}\)라고 하자.

그러면 \(\overline{x}\)에 대한 계의 모멘트는 \[\sum_{k=1}^{3} m_k (x_k - \overline{x} )\] 이 된다. 이 값이 \(0\)이면 지렛대는 평형상태가 되므로 \[\sum_{k=1}^{3} m_k (x_k - \overline{x} ) =0\] 즉 \[\overline{x} = \frac{\sum x_k m_k }{\sum m_k} = \frac{\text{(system moment about origin)}}{\text{(system mass)}}\] 를 얻는다. 이때 \(\overline{x}\)를 질량중심(center of mass)이라고 부른다.
(2) 평면에 놓인 유한 개의 물체
평면에서도 이와 비슷한 방법으로 모멘트와 질량중심을 계산할 수 있다. 좌표평면에 \(n\)개의 물체가 놓여 있고, 각 물체의 질량과 위치는 각각 \(m_k ,\) \((x_k ,\, y_k ) \)라고 하자.
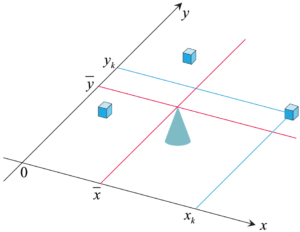
이 상황에서는 \(x\)축에 대한 모멘트와 \(y\)축에 대한 모멘트를 생각할 수 있다. \(x\)축을 기준으로 했을 때 한 물체의 토크는 \(g y_k m_k\)이므로 \(x\)축에 대한 계의 토크는 \[\sum_{k=1}^{n} gy_k m_k \] 이며, \(x\)축에 대한 계의 모멘트는 \[M_x = \sum_{k=1}^{n} y_k m_k\] 이다. 또한 계의 질량은 각 물체의 질량의 합과 같으므로 \[M = \sum_{k=1}^{n} m_k\] 이다. 그러므로 계의 질량중심의 \(y\)좌표는 \[\overline{y} = \frac{M_x}{M} = \frac{\sum y_k m_k }{\sum m_k}\] 이다. 비슷한 방법으로 \(y\)축에 대한 계의 모멘트는 \[M_y = \sum_{k=1}^{n} x_k m_k\] 이며, 계의 질량중심의 \(x\)좌표는 \[\overline{x} = \frac{M_y}{M} = \frac{\sum x_k m_k }{\sum m_k}\] 이다.
(3) 평면에 놓인 물체
아래 그림에서처럼 평면에 얇고 평평한 물체가 놓여 있다고 하자. 물체는 매끄러운 곡선으로 둘러싸인 모양이다.
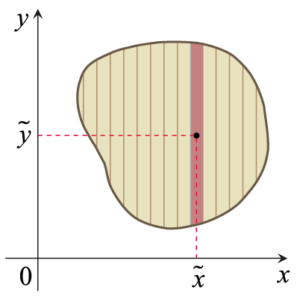
이 물체를 \(y\)축에 평행한 직선으로 잘라서 여러 개의 띠(strip)가 되도록 하자. [물론 이 띠는 직사각형 모양이 아니지만, (구분구적법으로 정적분을 계산할 때처럼) 폭이 아주 작은 직사각형이라고 생각해도 무방하다.] 각 띠의 질량중심은 \((\tilde{x} ,\, \tilde{y} )\)이고 질량은 \(\Delta x\)라고 하자. 각 띠를 하나의 물체로 생각하면 물체 전체의 질량중심의 좌표 \((\overline{x} ,\, \overline{y} )\)는 다음과 같이 구할 수 있다. \[\overline{x} = \frac{M_y}{M} = \frac{\sum \tilde{x} \Delta m}{\sum \Delta m} ,\quad \overline{y} = \frac{M_x}{M} = \frac{\sum \tilde{y} \Delta m}{\sum \Delta m} .\] 여기서 각 띠의 폭이 무한히 작아지는 극한, 즉 \(\Delta m \,\to\,0\)인 극한을 생각하면 위 공식에서 각각의 합은 적분이 되므로, 물체 전체의 질량중심의 좌표는 다음과 같이 구할 수 있다. \[\overline{x} = \frac{\int \tilde{x} \,dm}{\int dm} ,\quad \overline{y} = \frac{\int \tilde{x} \,dm}{\int dm} .\] 지금까지 살펴본 내용을 정리하면 다음과 같다.
정의 1. (평면에 놓인 물체의 모멘트와 질량중심)
\[\begin{align} \text{Moment about the \(x\)-axis:} \quad & M_x = \int \tilde{y} \, dm \\[6pt] \text{Moment about the \(y\)-axis:} \quad & M_y = \int \tilde{x} \, dm \\[6pt] \text{Mass:} \quad & M = \int \, dm \\[6pt] \text{Center of mass:} \quad & \overline{x} = \frac{M_y}{M} ,\,\, \overline{y} = \frac{M_x}{M} \end{align}\]예제 1. 좌표평면에서 포물선 \(y=4-x^2\)과 \(x\)축으로 둘러싸인 영역에 놓인 얇은 판의 질량중심을 구하시오. 단, \((x,\,y)\)에서의 밀도는 \(\delta = 2x^2\)이다.
풀이. 구하고자 하는 질량중심의 좌표를 \((\overline{x} ,\, \overline{y} )\)라고 하자. 일단 주어진 영역의 모양과 밀도함수가 모두 \(y\)축에 대칭이므로 \(\overline{x} =0 \)이다. 이제 \(\overline{y}\)만 구하면 된다.
주어진 영역을 \(y\)축에 평행한 직선으로 잘라 띠를 만들자. 그 모양은 아래 그림과 같다.
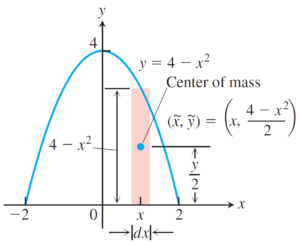
하나의 띠는 가로의 길이 \(dx\)가 \(0\)에 가까운 모양이라고 생각하면 된다. 각 띠의 질량중심을 \((\tilde{x} ,\, \tilde{y} )\)라고 하자. 띠의 가로의 길이가 \(0\)에 가깝고 밀도함수는 연속함수이므로 \(\tilde{x} = x\)인 것으로 두어도 무방하다. 한편 밀도함수는 \(y\)좌표에 영향을 받지 않으므로 띠의 세로의 반에 해당하는 부분이 \(\tilde{y}\)가 된다. 즉 \[\tilde{x} = x ,\,\,\, \tilde{y} = \frac{4-x^2}{2}\] 이다. \(\overline{y}\)를 구하려면 \(x\)축에 대한 모멘트를 계산해야 한다. 먼저 이 띠의 질량은 \[dm = dx \times (4-x^2 ) \times \delta = 2x^2 (4-x^2 ) dx \] 이다. 또한 이 띠의 질량중심이 \(x\)축으로부터 떨어진 거리는 \(\tilde{y}\)이다. 따라서 \[\begin{align} M_x &= \int \tilde{y} dm \\[4pt] &= \int_{-2}^{2} \frac{4-x^2}{2} \cdot 2x^2 \cdot (4-x^2 ) dx \\[4pt] &= \int_{-2}^{2} (16x^2 - 8x^4 + x^6 ) dx = \frac{2048}{105} \end{align}\] 이다. 그러므로 \[\overline{y} = \frac{M_x}{M} = \frac{2048}{105} \cdot \frac{15}{256} = \frac{8}{7}\] 이다.
(Thomas’ Calculus Global Edition 13판 6.6절에서 발췌함.)
(4) 평면에서 두 곡선으로 둘러싸인 영역
좌표평면에 놓인 평평한 판이 두 함수 \(y=f(x)\)와 \(y=g(x)\)의 그래프, 그리고 두 직선 \(x=a,\) \(x=b\)로 둘러싸인 모양이라고 하자. 그리고 평면 위의 각 점에서 밀도가 \(\delta\)라고 하자. [단, \(\delta\)는 \(y\)좌표에 영향을 받지 않고 오직 \(x\)만을 변수로 취하는 함수라고 하자.] 이 판의 질량중심을 구하기 위하여, 아래 그림과 같이 \(y\)축에 평행한 직선으로 잘라 띠를 만들자.
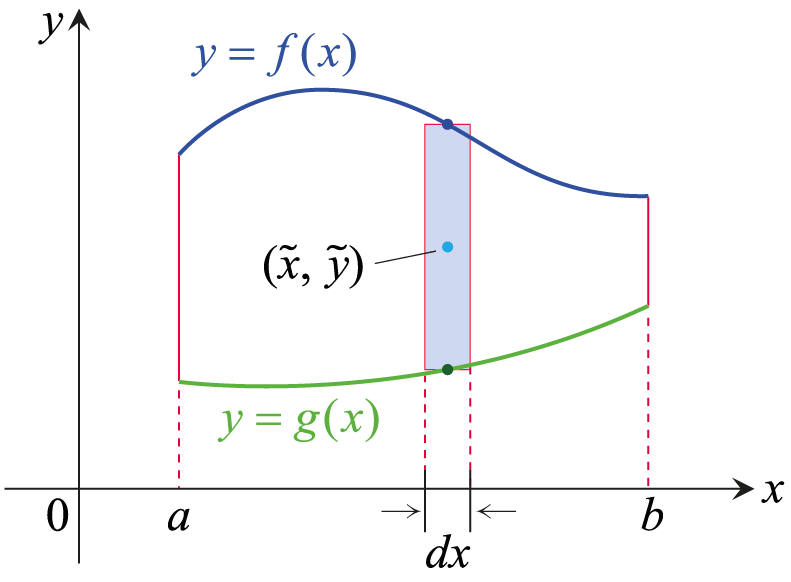
이 띠의 질량중심은 \[(\tilde{x} ,\,\tilde{y}) = \left( x ,\, \frac{1}{2} [f(x)+g(x)] \right)\] 이다. 이 띠의 가로 길이는 \(dx\)이며 길이(높이)는 \((f(x)-g(x))\)이다. 그러므로 이 띠의 넓이는 \[dA = [f(x)-g(x)]dx\] 이며, 이 띠의 질량은 \[dm = \delta \,dA = \delta [ f(x)-g(x)]dx\] 이다. 따라서 \(y\)축에 대한 판의 모멘트는 \[M_y = \int x\,dm = \int_a^b x \delta [f(x)-g(x)]dx\] 이며, \(x\)축에 대한 판의 모멘트는 \[\begin{align} M_x &= \int y\, dm \\[4pt] &= \int_a^b \frac{1}{2} [f(x)+g(x)] \cdot \delta [f(x)-g(x)]dx\\[4pt] &= \int_a^b \frac{\delta}{2} [(f(x))^2 - (g(x))^2 ] dx \end{align}\] 이다. 그러므로 판 전체의 질량중심 \((\overline{x} ,\, \overline{y} )\)의 좌표는 다음과 같다.
정리 1. (두 함수의 그래프로 둘러싸인 판 모양의 질량중심)
\[\begin{align} \overline{x} &= \frac{1}{M} \int_a ^b \delta x [f(x)-g(x)] dx, \\[4pt] \overline{y} &= \frac{1}{M} \int_a ^b \delta [(f(x))^2 - (g(x))^2 ]dx. \end{align}\]밀도함수가 상수일 때 물체의 질량중심을 그 물체의 모양중심(centroid) 또는 무게중심이라고 부른다.
예제 2. 평면에서 포물선 \(y=x^2\)과 직선 \(y=x\)로 둘러싸인 영역의 모양중심을 구하시오.
풀이. \(\delta = 1\)로 두고 정리 1의 공식을 이용하자. 먼저 영역의 넓이는 \[M = \int_0^1 (x-x^2 )dx = \frac{1}{6}\] 이며, 모멘트는 \[\begin{align} M_x &= \int_0^1 \frac{1}{2}(x+x^2)(x-x^2) dx = \frac{1}{15} , \\[6pt] M_y &= \int_0^1 x(x-x^2)dx = \frac{1}{12} \end{align}\] 이다. 그러므로 영역의 모양중심 \((\overline{x} ,\, \overline{y} )\)의 좌표는 \[\overline{x} = \frac{M_y}{M} = \frac{1}{2} ,\,\,\, \overline{y} = \frac{M_x}{M} = \frac{2}{5}\] 이다.
(5) 평면에 놓인 곡선
곡선으로 둘러싸인 영역의 질량중심뿐만 아니라 곡선의 질량중심도 구할 수 있다.
예제 3. 중심이 원점이고 반지름이 \(a > 0\)이며 상반평면에 놓인 반원 \(y=\sqrt{a^2 - x^2}\)의 모양중심을 구하시오.
풀이. 밀도함수를 \(\delta = 1\)이라고 두자. 반원의 모양중심의 좌표를 \((\overline{x} ,\, \overline{y})\)라고 하자. 반원이 \(y\)축에 대칭이므로 \(\overline{x} =0\)이다. 이제 \(\overline{y}\)만 구하면 된다.
반원을 작은 호(arc) 조각으로 나누자. 하나의 호 조각의 질량중심을 \((\tilde{x} ,\, \tilde{y})\)라고 하자. 그러면 \(\tilde{y} = a\sin\theta\)라고 나타낼 수 있으며, 호 조각의 길이는 \(ds = a d\theta\)라고 나타낼 수 있다. 이 호 조각의 질량은\[dm = \delta \,ds = a\,d\theta\]이다. 또한 호 조각의 질량중심이 \(x\)축으로부터 떨어진 거리는\[\tilde{y} = a\sin \theta\]이다. 그러므로 \[ \overline{y} = \frac{\int \tilde{y} \,dm}{\int dm} = \frac{\int_0^{\pi} a \sin \theta \cdot a \,d\theta}{\int_0^{\pi} a\,d\theta} = \frac{2a^2}{a\pi} = \frac{2a}{\pi} \] 이다. (Thomas’ Calculus Global Edition 13판 6.6절에서 발췌함.)
회전체의 부피와 넓이에 대한 파푸스의 정리
4세기 경 알렉산드리아의 수학자 파푸스는 도형의 모양중심을 이용하여 회전체의 부피와 넓이를 구하는 방법을 고안하였다.
정리 2. (회전체의 부피에 대한 파푸스의 정리)
평면에 넓이가 \(A\)인 도형이 있다. 이 도형이 도형을 관통하지 않고 동일평면에 놓인 직선 \(\ell\)을 축으로 회전하여 만든 회전체의 부피는 도형의 모양중심이 직선 \(\ell\)을 축으로 회전하였을 때의 자취(원)의 길이에 도형의 넓이를 곱한 것과 같다. 즉 도형의 모양중심과 직선 \(\ell\)의 거리를 \(\rho\)라고 하면 회전체의 부피는 \[V = 2\pi \rho A\] 이다.
증명
도형이 연속인 곡선으로 둘러싸여 있고 볼록한 경우에 대하여 증명한다. 도형이 \(xy\)-평면의 제 1 사분면에 놓여 있고 \(x\)축을 축으로 회전한다고 하자. 주어진 도형을 \(x\)축에 평행한 직선으로 잘라 띠를 만들자. 띠가 \(x\)축으로부터 떨어진 거리를 \(\tilde{y} = y\)라고 하고, 띠의 길이를 \(L(y)\)라고 하자. 그러면 \(L(y)\)는 \(y\)를 변수로 하는 연속함수이다.
도형이 차지하는 영역의 \(y\)좌표의 범위가 \(c \le y \le d\)라고 하자. 그러면 이 도형을 \(x\)축에 대하여 회전한 회전체의 부피는 다음과 같다. \[\begin{align} V &= \int_c^d 2 \pi \text{(shell radius)(shell height)}dy \\[6pt] &= 2 \pi \int_c^d y\,L(y)\,dy. \end{align}\] 그러므로 도형의 모양중심의 \(y\)좌표는 \[\overline{y} = \frac{1}{A} \int_c^d \tilde{y} dA = \frac{1}{A} \int_c^d y \,L(y) \,dy\] 이다. 그러므로 \[V = 2\pi \int_c^d y\,L(y) \,dy = 2\pi A\overline{y} = 2\pi \rho A\] 이다.
정리 3. (회전체의 넓이에 대한 파푸스의 정리)
평면에 길이가 \(L\)인 곡선이 있다. 이 곡선이 동일평면에 놓여 있고 곡선을 지나지 않는 직선 \(\ell\)을 축으로 회전하여 만든 회전체의 넓이는 곡선의 모양중심이 직선 \(\ell\)을 축으로 회전하였을 때의 자취(원)의 길이에 곡선의 길이를 곱한 것과 같다. 즉 곡선의 모양중심과 직선 \(\ell\)의 거리를 \(\rho\)라고 하면 회전체의 넓이는 \[S = 2\pi \rho L\] 이다.
증명
곡선이 매끄러운 경우(미분 가능한 함수의 그래프인 경우)에 대하여 증명한다. 곡선이 \(xy\)-평면의 제 1 사분면에 놓여 있고, 좌표평면에서 이 곡선이 차지하는 영역의 \(x\)좌표의 범위가 \(a \le x \le b\)라고 하자. 그리고 이 곡선이 \(x\)축을 축으로 회전한다고 하자.
곡선을 여러 개의 호 조각으로 나눈다. 그 중 한 조각을 생각하자. 호 조각의 길이를 \(ds\)라고 하고, 호 조각이 \(x\)축으로부터 떨어진 거리를 \(\tilde{y} = y\)라고 하자. 곡선이 매끄럽고 호 조각의 길이가 매우 짧으므로, 이 호 조각이 회전한 자취의 넓이는 \(2\pi y \,ds\)와 같다. 그러므로 곡선을 회전한 회전체의 넓이는 \[S = \int_{x=a}^{y=b} 2\pi y\,ds = 2\pi \int_{x=a}^{x=b} y\,ds\] 이다. 한편 곡선의 모양중심의 \(y\)좌표는 \[\overline{y} = \frac{\int_{x=a}^{x=b} \tilde{y} \,ds}{\int_{x=a}^{x=b} ds} = \frac{1}{L} \int_{x=a}^{x=b} y\,ds\] 이다. 그러므로 \[S = 2\pi \int_{x=a}^{x=b} y\,ds = 2\pi \overline{y} L = 2\pi \rho L\] 이다.
4세기는 미적분의 개념이 정립되기 한참 전인데, 이러한 방법을 고안해냈다는 것은 참 대단한 일이다.
예제 4. 좌표평면에서 중심이 \((b,\,0)\)이고 반지름의 길이가 \(a\)인 원을 \(y\)축을 축으로 회전시킨 회전체(원환면)의 부피와 겉넓이를 구하시오. (단, \(b > a > 0.\))
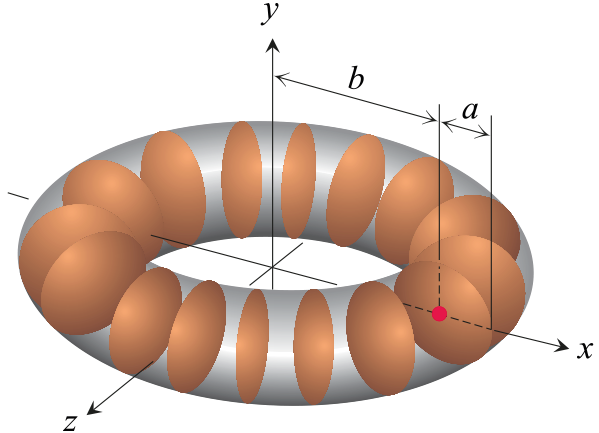
풀이. 주어진 원은 중심이 곧 모양중심이므로, 모양중심과 회전축의 거리는 \(b\)이다. 또한 이 원의 넓이는 \(\pi a^2\)이며, 원의 둘레의 길이는 \(2\pi a\)이다. 그러므로 문제의 원환면의 부피는 \[V = 2\pi b \times \pi a^2 = 2 \pi^2 a^2 b\] 이며, 원환면의 겉넓이는 \[S = 2\pi b \times 2\pi a = 4\pi^2 ab\] 이다. (Thomas’ Calculus Global Edition 13판 6.6절의 그림을 사용함.)
예제 5. \(xy\)-평면에서 포물선 \(y=x^2\)과 직선 \(y=x\)로 둘러싸인 영역 \(R\)를 직선 \(y=x\)를 축으로 회전한 회전체의 부피를 구하시오.
풀이. 예제 2에서 \(R\)의 모양중심은 \((\overline{x} ,\, \overline{y}) = (\frac{1}{2} ,\, \frac{2}{5})\)이며, \(R\)의 넓이는 \(\frac{1}{6}\)이다. 모양중심이 직선 \(y=x\)와 떨어진 거리는, 점 \(\left(\frac{1}{2}, \, \frac{2}{5}\right)\)와 직선 \(x-y=0\) 사이의 거리 공식에 의하여 \[\rho = \frac{\left\lvert \frac{1}{2} - \frac{2}{5} \right\rvert}{\sqrt{2}} = \frac{1}{10\sqrt{2}}\] 이다. 그러므로 회전체의 부피는 \[V = 2\pi \times \frac{1}{10\sqrt{2}} \times \frac{1}{6} = \frac{\sqrt{2}}{60}\pi\] 이다.
예제 6. 네 점 \(\mathrm{A}(0,\,2),\) \(\mathrm{B}(2,\,0),\) \(\mathrm{C}(4,\,2),\) \(\mathrm{D}(2,\,4)\)를 꼭짓점으로 하는 사각형 \(\mathrm{ABCD}\)를 직선 \(\sqrt{3} (y+2) = x-2\)를 축으로 회전하여 얻은 회전체의 겉넓이를 구하시오.
풀이. 사각형 \(\mathrm{ABCD}\)은 정사각형이므로 이 사각형의 모양중심은 두 대각선의 교점 \((2,\,2)\)이다. 이 점이 회전축 \[x-\sqrt{3} y - 2-2\sqrt{3} =0\]과 떨어진 거리는\[\rho = \frac{\left\lvert 2-2\sqrt{3} -2-2\sqrt{3}\right\rvert}{\sqrt{1+3}} = 2\sqrt{3}\]이다. 한편 사각형 \(\mathrm{ABCD}\)의 둘레 길이는 \(8\sqrt{2}\)이다. 그러므로 회전체의 겉넓이는 \[S = 2\pi \times 2\sqrt{3} \times 8\sqrt{2} = 32\sqrt{6} \pi\] 이다.
첨언
이 포스트에서는 평면에 놓인 물체의 질량중심을 구할 때 밀도함수 \(\delta\)가 \(y\)좌표에 영향을 받지 않고 \(x\)만을 변수로 취하는 함수인 경우만을 다루었다. \(\delta\)가 \(x\)좌표와 \(y\)좌표 모두에 영향을 받는 2변수 함수일 때 질량중심을 구하려면 중적분을 사용해야 한다.
