\(x\)축에서 한 점 \(c\)에 다가갈 수 있는 방향은 두 가지가 있다. 즉 \(c\)의 왼쪽에서 \(c\)에 다가갈 수도 있으며, \(c\)의 오른쪽에서 \(c\)에 다가갈 수도 있다. 이와 같이 \(x\)가 \(c\)에 다가가는 방향에 따라 \(c\)에서 \(f\)의 극한을 구분할 수 있다.
좌극한과 우극한의 정의
\(x\)가 \(c\)의 왼쪽에서 \(c\)에 접근할 때 \(f(x)\)의 값이 \(L\)에 다가가면 \(f\)는 \(c\)에서 좌극한 \(L\)을 가진다고 말한다. 우극한에 대해서도 비슷한 방법으로 정의한다. 논리적인 정의는 다음과 같다.
정의 1. (좌극한과 우극한)
- \(L\)과 \(c\)가 실수이고 함수 \(f : D \to \mathbb{R}\)가 \(c\)를 오른쪽 끝점으로 하는 한 열린 구간에서 정의되었다고 하자. 만약 임의의 \(\epsilon > 0\)에 대하여 \(\delta > 0\)이 존재하여 \(0 < c-x < \delta\)인 모든 \(x \in D\)에 대하여 \(|f(x)-L| < \epsilon\)이 성립하면 ‘\(f\)는 \(c\)에서 좌극한 \(L\)을 가진다’라고 말하고, \[f(x) \,\to\, L \quad \text{as} \quad x \,\to\, c^{-}\] 또는 \[\lim_{x\,\to\,c^{-}} f(x) = L\] 또는 \[f(c^- ) = L\] 로 나타낸다.
- \(L\)과 \(c\)가 실수이고 함수 \(f : D \to \mathbb{R}\)가 \(c\)를 왼쪽 끝점으로 하는 한 열린 구간에서 정의되었다고 하자. 만약 임의의 \(\epsilon > 0\)에 대하여 \(\delta > 0\)이 존재하여 \(0 < x-c < \delta\)인 모든 \(x \in D\)에 대하여 \(|f(x)-L| < \epsilon\)이 성립하면 ‘\(f\)는 \(c\)에서 우극한 \(L\)을 가진다’라고 말하고, \[f(x) \,\to\, L \quad \text{as} \quad x \,\to\, c^{+}\] 또는 \[\lim_{x\,\to\,c^{+}} f(x) = L\] 또는 \[f(c^+ ) = L\] 로 나타낸다.
극한값이 존재하지 않는 곳에서도 좌극한이나 우극한은 존재할 수 있다.
보기 1. 함수 \(f\)가 다음과 같이 주어졌다고 하자. \[f(x) = \begin{cases} 7 \quad &\text{if} \,\, x > 1 \\[8pt] 0 \quad &\text{if} \,\, x \le 1 \end{cases}\] 이 때 \(1\)에서 \(f\)의 극한값은 존재하지 않지만 \[\lim_{x\,\to\,1^-} f(x) = 0 ,\quad \lim_{x\,\to\,1^+} f(x) = 7\] 로서 \(1\)에서 \(f\)의 좌극한과 우극한은 각각 존재한다.
함수가 구간에서 정의되어 있을 때 구간의 왼쪽 끝점에서는 우극한과 극한을 동일시하며, 구간의 오른쪽 끝점에서는 좌극한과 극한을 동일시한다.
보기 2. 함수 \(f\)가 반열린 구간 \((3,\,5]\)에서 \(f(x) = x^2\)으로 정의되어 있다고 하자. 이 때 \[\lim_{x\,\to\,3} f(x) = \lim_{x\,\to\,3^+} f(x) = 9 ,\] \[\lim_{x\,\to\,5} f(x) = \lim_{x\,\to\,5^-} f(x) = 25 \] 이다. 또한 \(3 < c < 5\)인 점 \(c\)에 대해서는 \[\lim_{x\,\to\,c} f(x) = \lim_{x\,\to\,c^-} f(x) = \lim_{x\,\to\,c^+} f(x) = c^2 \] 이다.
한방향 극한과 양방향 극한의 관계
좌극한과 우극한을 통틀어 한방향 극한이라고 부른다. 한방향 극한과 구분하기 위하여 일반적인 극한을 양방향 극한이라고 부른다.
보기 2에서 본 것처럼 함수의 정의역이 구간일 때, 구간의 왼쪽 끝점에서는 극한과 우극한이 동일한 개념이며, 구간의 오른쪽 끝점에서는 극한과 좌극한이 동일한 개념이다.
그러므로 양방향 극한이라는 용어는 \(f\)가 \(c\)를 원소로 갖는 한 열린구간의 \(c\)를 제외한 모든 점에서 정의되었을 때, 즉 \(x\)가 \(c\)의 왼쪽으로부터 \(c\)에 다가갈 수 있고, \(c\)의 오른쪽으로부터도 \(c\)로 다가갈 수 있는 상황에서만 사용하기로 한다.
정리 1. \(c\)와 \(L\)이 실수이고 함수 \(f\)가 \(c\)를 원소로 갖는 한 열린구간의 \(c\)를 제외한 모든 점에서 정의되었다고 하자. 이 때 \[\lim_{x\,\to\,c} f(x) = L\] 일 필요충분조건은 \[\lim_{x\,\to\,c^-} f(x) = L \quad \text{and} \quad \lim_{x\,\to\,c^+}f(x)=L\] 인 것이다.
증명
먼저 필요조건을 증명하자. \(c\)에서 \(f\)의 극한값이 \(L\)이라고 가정하자. 그리고 \(\epsilon > 0\)이 임의로 주어졌다고 하자. 극한의 정의에 의하여 \(\delta > 0\)이 존재하여 \(0 < |x-c| < \delta\)인 임의의 \(x\)에 대하여 \[ |f(x)-L| < \epsilon\tag{1}\] 이 성립한다. 그런데 \[0 < c-x < \delta\tag{2}\] 또는 \[0 < x-c < \delta\tag{3}\] 어느 때나 \(0 < |x-c| < \delta\)가 성립하므로 (1)이 성립한다. 그러므로 (2), (1)에 의하여 \[\lim_{x\,\to\,c^-} f(x) = L\] 이며, (3), (1)에 의하여 \[\lim_{x\,\to\,c^+} f(x) = L\] 이다.
다음으로 충분조건을 증명하자. \(c\)에서 \(f\)의 좌극한과 우극한이 모두 \(L\)이라고 가정하자. 그리고 \(\epsilon > 0\)이 임의로 주어졌다고 하자. 좌극한의 정의에 의하여 \(\delta_1 > 0\)이 존재하여 \[0 < c-x < \delta_1\tag{4}\] 인 임의의 \(x\)에 대하여 \(|f(x)-L| < \epsilon\)이 성립하며, 우극한의 정의에 의하여 \(\delta_2 > 0\)가 존재하여 \[0 < x-c < \delta_2\tag{5}\] 인 임의의 \(x\)에 대하여 \(|f(x) - L| < \epsilon\)이 성립한다.
\(\delta = \min \left\{ \delta_1 ,\, \delta_2 \right\}\)라고 하자. 그러면 \(0 < |x-c| < \delta\)인 \(x\)는 (4) 또는 (5) 중 하나를 반드시 만족시키므로, 그러한 \(x\)에 대하여 \(|f(x) - L| < \epsilon\)이 성립한다.
한방향 극한의 예: \((\sin x )/ x\)의 극한
삼각함수의 성질을 증명할 때 자주 사용되는 극한 공식을 하나 살펴보자.
정리 2. (\((\sin \theta )/\theta\)의 극한) \[\lim_{\theta \to 0} \frac{\sin \theta}{\theta} = 1 \qquad ( \theta \text{ in radians}) \tag{6}\]
증명
\(\theta =0\)에서 \((\sin \theta )/\theta \)의 좌극한과 우극한의 값이 모두 \(1\)임을 보이자. 먼저 \(0 < \theta < \pi /2\)인 경우를 살펴보자.
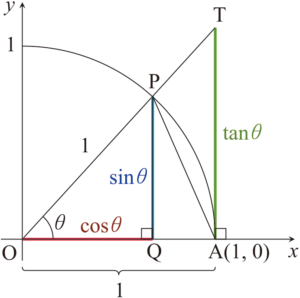
그림와 같이 좌표펴면의 제 1 사분면에 반지름이 \(1\)이고 원점이 중심인 사분원을 그린다. 그리고 \(\angle \mathrm{POA} = \theta\)가 되도록 사분원 위의 점 \(\mathrm{P}\)를 잡는다. 점 \(\mathrm{P}\)에서 \(x\)축에 내린 수선의 발을 \(\mathrm{Q}\)라고 하고, 점 \(\mathrm{A}(1,\,0)\)을 지나고 \(x\)축과 수직인 직선이 반직선 \(\mathrm{OP}\)와 만나는 점을 \(\mathrm{T}\)라고 하자. 그러면 \[\sin \theta = \overline{\mathrm{PQ}} ,\quad \cos \theta = \overline{\mathrm{OQ}} ,\quad \tan \theta = \overline{\mathrm{TA}}\] 이다. 그런데 \[(\text{Area } \triangle \mathrm{OAP}) \le (\text{Area sector } \mathrm{OAP}) \le (\text{Area }\triangle \mathrm{OAT} )\] 이므로 \[\frac{1}{2} \sin \theta \le \frac{1}{2}\theta \le \frac{1}{2} \tan \theta \] 이다. \(0 < \theta < \pi / 2\)의 범위에서 위 부등식의 각 항은 모두 양수이므로, 각 항에 \(2\)를 곱하고 각 항을 \(\sin \theta\)로 나누면 \[1 < \frac{\theta}{\sin \theta } < \frac{1}{\cos \theta}\] 이며, 세 항의 역수를 취하면 \[1 > \frac{\sin\theta}{\theta} > \cos\theta \] 를 얻는다. 그런데 \(\theta \,\to\, 0^+\)일 때 \(\cos \theta \,\to\,1\)이므로, 위 부등식과 샌드위치 정리에 의하여 \[\lim_{\theta \,\to\,0^+} \frac{\sin\theta}{\theta} = 1\] 을 얻는다. 한편 \((\sin \theta)/\theta\)는 우함수이므로 \(0\)에서 이 함수의 좌극한과 우극한은 일치한다. 그러므로 \[\lim_{\theta \,\to\,0} \frac{\sin\theta}{\theta} = 1\] 을 얻는다.
보기 3. 다음 극한값을 구해 보자. \[\lim_{h\to 0}\frac{\cos h -1}{h} \] \(\cos h = 1 - 2 \sin ^2 (h/2)\)이므로 정리 2에 의하여 \[\begin{align} \lim_{h\to 0} \frac{\cos h -1}{h} &= \lim_{h\to 0}\frac{- \sin^2 (h/2)}{h/2} \\[6pt] &= -\lim_{\theta \to 0} \frac{\sin \theta}{\theta} \sin \theta \tag*{\(\leftarrow \, \theta = h/2 \)}\\[8pt] &= - 1 \times 0 = 0. \end{align}\]
보기 4. \(a \ne 0,\) \(b \ne 0\)일 때 다음 극한값을 구해 보자. \[\lim_{x\,\to\,0} \frac{\sin ax}{bx}\] 정리 2에 의하여 \[\begin{align} \lim_{x\,\to\,0} \frac{\sin ax}{bx} &= \lim_{x\,\to\,0} \frac{\sin ax}{ax} \cdot \frac{a}{b} \\[6pt] &= \frac{a}{b} \cdot \lim_{h\,\to\,0} \frac{\sin h}{h} \\[8pt] &= \frac{a}{b} \cdot 1 = \frac{a}{b}. \end{align}\]
