[수학Ⅰ] 제1장 집합과 논리의 기초(2)

4.2K

연역적 추론

두 조건 \(p, q\)에 대하여, 문장 '\(p\longrightarrow q\)'는 하나의 명제가 된다. 일반적으로 조건 \(p, q\)의 진리집합을 각각 \(P, Q\)라 할 때, \(p\longrightarrow q\)가 참이면 조건 \(p\)를 참이되게 하는 원소는 조건 \(q\)도 참이 되게 하므로 \(P\subset Q\)인 관계가 성립한다. 또한 \(P\subset Q\)인 관계가 있으면 명제 \(p\longrightarrow q\)는 참이다. 한편, 명제 \(p\longrightarrow q\)가 거짓이라는 것은 조건 \(p\)가 참이 되지만 \(q\)는 참이 되지 않는 원소가 있음을 말하며 이는 곧 \(P\not\subset Q\)임을 뜻한다. 이상을 정리하면 다음과 같다.

명제 \(p\longrightarrow q\)가 거짓임을 보이기 위해서는 \(p\)를 만족시키지만, \(q\)를 만족시키지 않는 예를 하나라도 보이면 된다. 즉 \(x\in P\)이고 \(x\not\in Q\)인 \(x\)가 있음을 보이면 된다. 이같은 예를 반례(counter example)라고 한다. 예를 들어 명제 \[ \mbox{\(x\)가 \(4\)의 약수이면 \(x\)는 \(6\)의 약수이다.} \] 의 반례로 \(4\)를 잡을 수 있다.

합성명제 중에는 \(\sim p\vee p\)와 같이 그 진릿값이 항상 참인 것이 있다. 그리고 \(\sim p\wedge p\)와 같이 그 진릿값이 항상 거짓인 것도 있다. 이렇게 모든 논리적 가능성의 각 경우마다 진릿값이 참인 명제를 항진명제(tautology)라고 한다. 그리고 모든 논리적 가능성의 각 경우마다 진릿값이 거짓인 명제를 모순명제(contradiction)라고 한다. 항진명제는 보통 \(t\)로 표기하고 모순명제는 보통 \(c\)로 표기한다.

두 명제 혹은 조건 \(p, q\)에 대하여 명제 \(p\longrightarrow q\)가 참일 때, 이를 \[ p\Longrightarrow q \] 와 같이 나타내며 '\(p\)는 \(q\)를 함의한다.'라고 읽는다. 이 때 \(p\)는 \(q\)이기 위한 충분조건이라고 하며 \(q\)는 \(p\)이기 위한 필요조건이라고 한다. 또한 쌍조건문 \(p\longleftrightarrow q\)가 참일 때 이것을 \(p\Longleftrightarrow q\)로 나타내고, '\(p\)와 \(q\)는 동치이다.’라고 한다. 이때 \(p\)는 \(q\)의 필요충분조건이며 \(q\)는 \(p\)의 필요충분조건이다. 보통 쌍조건문 \(p\Longleftrightarrow q\)는 다음과 같이 읽곤 한다.

• \(p\)와 \(q\)는 서로 필요충분조건이다.
• \(p\)이면 \(q\)이고 \(q\)이면 \(p\)이다.
• \(p\)이면 그리고 그때에만 \(q\)이다.

유제 1.10 \([(p\longrightarrow q)\wedge (q\longrightarrow r)]\Longrightarrow [p\longrightarrow r]\)임을 진리표를 이용하여 확인해 보아라.

기호 \(\Longleftrightarrow\)와 \(\equiv\)는 두 명제가 동치라는 것을 나타낼 때에도 사용되기도 하지만 어떠한 개념을 정의할 때에도 사용된다. 이를테면 부등호 \(\leq\)를 다음과 같이 정의할 수 있다.¹ \[ a\leq b\quad \Longleftrightarrow\quad (a< b \vee a=b) \] 이것은 다음과 같이 나타낼 수도 있다. \[ a\leq b \quad \equiv\quad (a< b \vee a=b) \]

보기 논리합, 논리곱, 쌍조건의 진리표를 작성해보면 다음과 같다. 이 진리표에 의해 \begin{align*} p\vee q\quad & \Longleftrightarrow\quad q\vee p, \\ p\wedge q\quad & \Longleftrightarrow\quad q\wedge p, \\ p\longleftrightarrow q\quad & \Longleftrightarrow\quad q\longleftrightarrow p \end{align*} 임을 알 수 있다. 즉 위의 표로부터 논리합, 논리곱, 쌍조건부는 교환법칙이 성립함을 확인할 수 있다.

유제 1.11 진리표를 이용하여 논리합과 논리곱의 분배법칙이 성립함을 보여라. 즉\begin{align*} p\wedge (q\vee r)\quad & \Longleftrightarrow\quad (p\wedge q)\vee (p\wedge r), \\ p\vee (q\wedge r)\quad & \Longleftrightarrow\quad (p\vee q) \wedge (p\vee r) \end{align*} 이 성립함을 보여라.

수학이나 논리에서의 정리(theorem)란 참인 명제들 중 중요한 사실을 일컫는 말이다. 이러한 참인 명제인 정리의 정당성을 밝히는 일을 증명(proof)이라고 한다. 보통 명제는 '\(\cdots\) 일 때 \(\cdots\)가 성립한다.'와 같이 조건(가정)과 결론으로 이루어져 있다. 수학에서 다루는 모든 정리가 \(p\Longrightarrow q\)의 꼴이라고 해도 과언이 아니다. 가정으로부터 결론까지 도달하는 과정을 논리적으로 설명할 때에는 정의, 그리고 기존에 증명했던 정리만을 사용해야 한다. 다음 상황을 생각해보자.

아름이는 자율학습시간에 수학 과제로 \[ (p\longrightarrow q)\quad \Longleftrightarrow\quad (\sim q\longrightarrow \sim p) \] 를 증명하려다가 옆자리에 앉은 고운이도 똑같은 숙제를 하고 있음을 발견하였다. 아름이는 진리표를 그리기가 귀찮아서 고운이에게 진리표를 보여 달라고 하였다. 그랬더니 고운이는 진리표를 그리지 않고 증명했다면서 아름이에게 다음과 같은 식을 보여주었다. \begin{align*} (p\longrightarrow q)\quad \Longleftrightarrow\quad (\sim p\ \vee q)\quad & \Longleftrightarrow\quad (q\ \vee\sim p) \\ & \Longleftrightarrow\quad [\sim(\sim q)\vee (\sim p)] \\ & \Longleftrightarrow\quad \sim q\longrightarrow \sim p \end{align*}

• 고운이가 보여준 식을 증명으로서 인정할 수 있는가?
• 진리표를 작성하는 것과 위와 같은 방법 중 어느 것이 더 간단하겠는가?

진리표를 사용하지 않고 정의, 전제로 인정한 명제, 이미 증명한 정리, 추론규칙 등을 활용하여 증명하는 것을 연역적 추론이라고 한다. 이제 몇 가지 추론규칙을 살펴보자.

Proof. 여기서는 (ⅲ)만 증명한다. \((p\vee q)\wedge\sim p\longrightarrow q\)의 진리표를 작성해보면 다음과 같다. 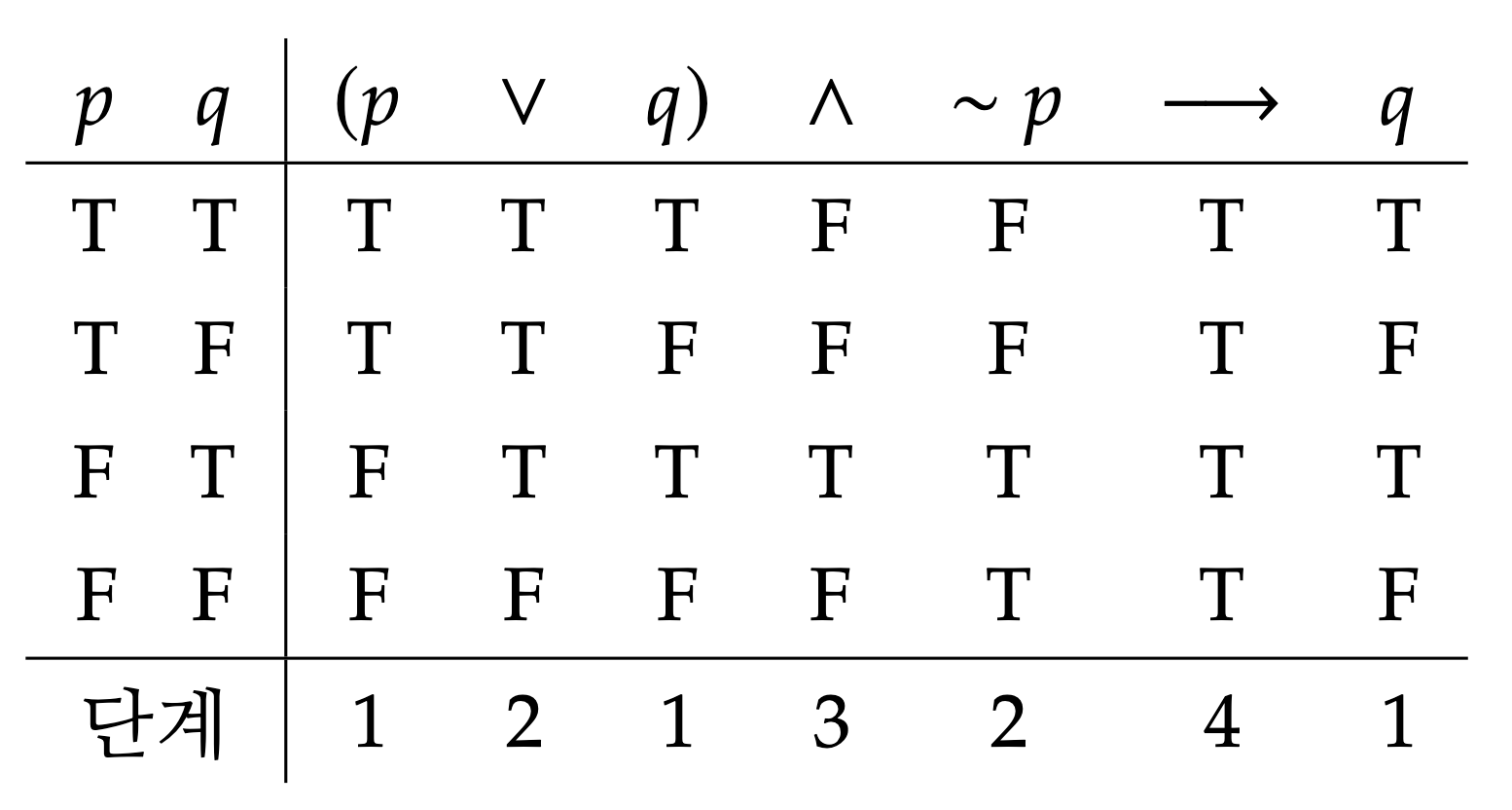따라서 \((p\vee q)\wedge\sim p\Longrightarrow q\)이다. 나머지 (ⅰ)과 (ⅱ)도 같은 방법으로 쉽게 증명할 수 있다.

위 정리에서 살펴본 추론규칙을 일상 언어로 표현하여 음미해 볼 수 있다. 예컨대 명제 \(p\)를 '나는 남자이다', \(q\)를 '나는 한국인이다.'라고 하면, 위 정리의 (ⅰ)의 명제는 '나는 남자이다. 따라서 나는 남자이거나 한국인이다.'가 된다. 또한 위 정리의 (ⅱ)의 명제는 '나는 남자이고 한국인이므로 나는 남자이다.'가 된다. 실생활에서는 사용되지 않는 큰 의미 없는 문장이지만 논리적으로 보면 참이다. 다음 추론규칙들도 증명에 자주 사용하는 규칙이다.

다음은 명제에 관한 드 모르간의 법칙으로 논리에서 편리한 수단으로 이용되고 있는 정리이다.

명제 '나는 감자를 좋아하거나 고구마를 좋아하거나 토마토를 좋아한다.'를 부정해보면 '나는 감자를 싫어하고 고구마도 싫어하며 토마토도 싫어한다.'가 된다. 또한, '나는 펭수이고 키가 210cm 이상이다.'를 부정하면 '나는 펭수가 아니거나 키가 210cm 미만이다.'가 되어 드 모르간의 법칙이 성립함을 음미해 볼 수 있다.

유제 1.12 다음 명제의 부정을 말하여라.

1. 토끼는 하얗지도 않고 귀엽지도 않다.
2. 비가 오면 우산이 잘 팔린다.
3. 애인이 생기면 학업 성적이 좋아진다.
4. 부업을 하면 돈은 벌지만 여유는 줄어든다.

다음 정리도 논리에 있어서 중요한 법칙들로 이미 증명했거나 혹은 쉽게 증명할 수 있는 것들이다.

결합법칙에 의하여 \[ (p\wedge q)\wedge r\quad\mbox{혹은}\quad p\wedge (q\wedge r) \] 에 있는 괄호는 불필요하게 된다. 즉 \(p\vee q\vee r\)과 \(p\wedge q\wedge r\)은 각각 일정한 뜻을 지닌다. 마찬가지로 명제 \(p_{1}, p_{2}, \ldots, p_{n}\)에 대하여 \(p_{1}\vee p_{2}\vee \cdots \vee p_{n}\)과 \(p_{1}\wedge p_{2}\wedge \cdots\wedge p_{n}\)의 의미도 자연스럽게 생각할 수 있다.

지금까지 살펴본 여러 가지 법칙들은 다음의 예제에서와 같이 논리적 동치 및 함의에 대한 정당성을 주장하는데 있어서 편리하게 사용할 수 있다. 이른바 추론규칙이라고 불리는 이들 법칙은 단지 편리하게 활용하고자 택한 것일 뿐 규칙 상호간의 독립성은 염두에 두지 않고 있다.

예제 1.13 대우법칙 \((p\longrightarrow q)\ \Leftrightarrow\ (\sim q\longrightarrow\sim p)\)를 연역적 추론을 통해 증명하여라.

Sol. \((p\longrightarrow q)\ \Leftrightarrow\ (\sim p\ \vee q)\ \Leftrightarrow\ (q\ \vee\sim p)\ \Leftrightarrow\ [\sim(\sim p)\vee (\sim p)] \ \Leftrightarrow\ \sim q\longrightarrow\ \sim p\)

조건명제 \(p\longrightarrow q\)에서 \(p\)를 가정이라고 하고 \(q\)를 결론이라고 하는데, 가정과 결론의 위치를 바꾼 \(q\longrightarrow p\)를 \(p\longrightarrow q\)의 역이라고 한다. 그리고 가정과 결론을 부정한 조건문 \(\sim p\longrightarrow\ \sim q\) 를 \(p\longrightarrow q\)의 이라고 한다. 또한, 가정과 결론을 부정하고 역을 취한 조건문 \(\sim q\longrightarrow\ \sim p\)를 \(p\longrightarrow q\)의 대우라고 한다. 조건명제의 역, 이, 대우 사이의 관계를 그림으로 표현하면 다음과 같다.

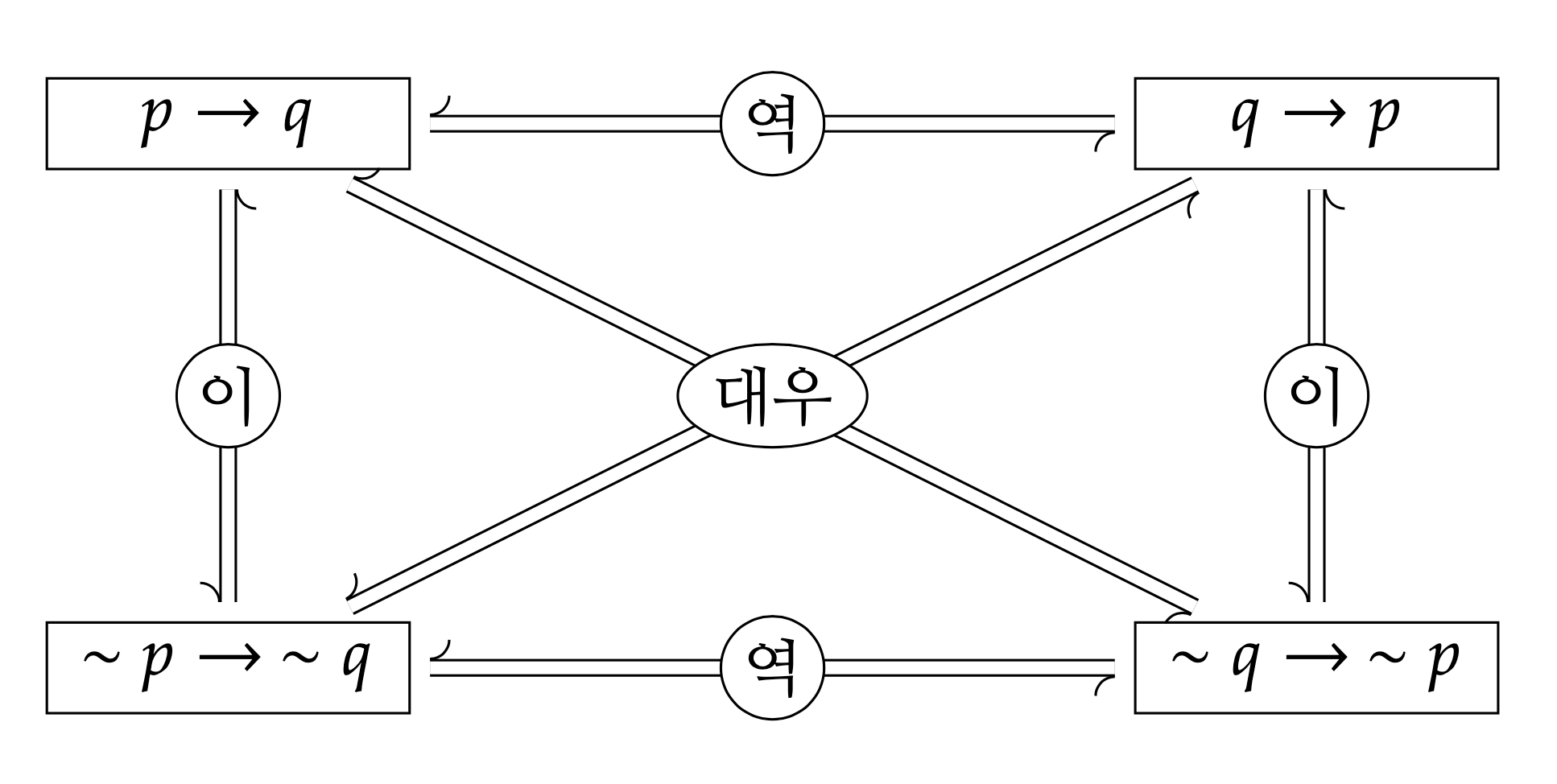
유제 1.14 다음 명제를 증명하여라. (진리표를 사용해도 좋고, 연역적으로 증명해도 좋다.)

1. \((p\longrightarrow q)\ \Longrightarrow\ (p\vee r \longrightarrow q\vee r) \)
2. \((p\longleftrightarrow q)\ \Longrightarrow\ (p\wedge q)\vee(\sim p\ \wedge \sim q) \)
3. \(\sim(p\wedge q\wedge r)\ \Longleftrightarrow\ \sim p\ \vee \sim q\ \vee \sim r \)
4. \(\sim (p\vee q\vee r)\ \Longleftrightarrow\ \sim p\ \wedge \sim q\ \wedge \sim r \)
5. \((p\vee q)\ \wedge\sim p\ \Longrightarrow q\)
6. \((p\longrightarrow q)\wedge (p\longrightarrow r)\ \Longleftrightarrow\ (p\longrightarrow q\wedge r)\)
7. \((p\longrightarrow q)\ \Longleftrightarrow\ (p\ \wedge\sim q\ \longrightarrow\ q\ \wedge\sim q)\)

앞서 예제 1.13에서 살펴본 바와 같이 어떠한 명제와 그 대우는 서로 동치이다. 명제 \(p\longrightarrow q\)가 참임을 증명하는 대신, '\(p\)는 참이고 \(q\)는 거짓이라고 하면 모순이다.'는 것을 보이기도 한다. 일상언어로 생각하면 매우 당연한 논리이지만, 형식적으로는 \[ (p\longrightarrow q)\ \Longleftrightarrow\ [ \sim(p\longrightarrow q)\longrightarrow c]\ \Longleftrightarrow\ (p\ \wedge\sim q)\longrightarrow c \] 와 같이 설명할 수 있다. ² 비슷하게 \[ p\ \Longleftrightarrow\ p\vee c\ \Longleftrightarrow\ \sim p\longrightarrow c \] 를 이용하여, 명제 \(p\)가 참임을 증명하는 대신, '\(p\)가 거짓이면 모순이다.'라는 것을 보이기도 한다. 이같은 증명 방법을 간접증명법 혹은 귀류법이라고 한다.

예제 1.15 자연수 \(n\)에 대하여, \(n^2\)이 짝수이면 \(n\)도 짝수임을 보여라.

Sol. 증명하고자 하는 명제의 대우, 즉 \[ \mbox{\(n\)이 홀수이면 \(n^{2}\)은 홀수이다.} \] 를 보이면 된다. \(n\)이 홀수이면, \(n=2k-1\ (k\in \mathbb{N})\)로 둘 수 있다. 이때 \[ n^{2}=(2k-1)^{2}=2(2k^{2}-2k)+1 \] 이므로 \(n^{2}\)도 홀수이다.

유제 1.16 \(\sqrt{2}\)가 무리수임을 보여라. ³

집합의 연산

집합에서의 연산이란 기존의 집합으로 새로운 하나의 집합을 구성하는 것을 뜻한다. 집합의 연산 중 가장 기본이 되는 이항연산(binary operation)을 다음과 같이 정의한다.

두 집합 \(A, B\)에 대하여, 이들 두 집합에 공통으로 속하는 원소가 하나도 없을 때, 즉 \[ A\cap B=\varnothing \] 일 때, 집합 \(A\)와 집합 \(B\)는 서로소(disjoint)라고 한다.

유제 1.17 집합 \(\{ x\mid \mbox{\(x\)는 \(3\leq x\leq 6\)을 만족시키는 자연수}\}\)의 진부분집합 중 집합 \(\{2, 3, 4\}\)와 서로소인 것을 모두 구하여라.

유제 1.18 집합 \(\{a, b, c, d\}\)의 부분집합 \(X\)에 대하여 \(c\in X\)이고 \(\{a, e\}\)와 서로소인 집합 \(X\)를 모두 구하여라.

두 유한집합 \(A, B\)에 대하여 \[ n(A\cup B)=n(A)+n(B)-n(A\cap B) \] 가 성립함을 알 수 있다. 또한 \(A, B\)가 서로소일 필요충분조건은 \(n(A\cup B)=n(A)+n(B)\)인 것도 확인 할 수 있다.

한편 집합의 이론에서 자주 사용하는 다음의 일항연산(unary operation)도 있다.

이 정의로부터 \[ A-B=A\cap B^{\mathrm{C}} \] 가 성립함을 알 수 있다. 또한 조건 \(p\)의 진리집합이 \(P\)라면 \(\sim p\)의 진리집합은 \(P^{\mathrm{C}}\)가 된다. 여집합과 관련하여 다음이 성립함을 알 수 있다.

Proof. 여기서는 (ⅲ)만 증명한다. \[ x\in (A^{\mathrm{C}})^{\mathrm{C}}\ \Longleftrightarrow\ \sim(x\in A^{\mathrm{C}})\ \Longleftrightarrow\ \sim(\sim (x\in A))\ \Longleftrightarrow\ x\in A \] 이므로 원하는 결과를 얻는다.

유제 1.19 정리 1.1.11의 나머지 등식들을 증명하여라.

합집합과 교집합은 다음과 같은 성질들을 갖는다.

Proof. 드 모르간의 법칙 \((A\cup B)^{\mathrm{C}}=A^{\mathrm{C}}\cap B^{\mathrm{C}}\)만 증명한다. \begin{align*} x\in (A\cup B)^{\mathrm{C}}\ &\Longleftrightarrow\ \sim (x\in A\ \vee\ x\in B) \\ & \Longleftrightarrow\ (x\not\in A)\wedge (x\not\in B) \\ & \Longleftrightarrow\ (x\in A^{\mathrm{C}})\wedge (x\in B^{\mathrm{C}}) \\ & \Longleftrightarrow\ x\in A^{\mathrm{C}}\cap B^{\mathrm{C}} \end{align*} 이므로 원하는 결과를 얻는다.

유제 1.20 정리 1.1.12의 나머지 등식들을 증명하여라.

유제 1.21 전체집합 \(U\)의 부분집합 \(A, B, C\)에 대하여 집합의 연산법칙을 이용하여 등식 \[ (A-B)\cap (A\cap C^{\mathrm{C}})=A-(B\cup C) \] 가 성립함을 보여라.

유제 1.22 전체집합 \(U=\{ 1, 2, \ldots, 10\}\)의 두 부분집합 \(A, B\)에 대하여 \[ A=\{ 3, 5, 10\},\quad A^{\mathrm{C}}\cap B^{\mathrm{C}}=\{ 1, 4, 6, 8\} \] 를 만족시키는 집합 \(B\)의 개수를 구하여라.

한정규칙

'모든'이나 '어떤'이 있는 명제

일반적으로 조건 \(p(x)\)는 \(x\)의 값이 무엇이냐에 따라 참, 거짓이 판별된다. 그러나 \(x\)앞에 '모든'이나 '어떤'과 같은 한정술사(quantifier)를 이용해 \(x\)의 값의 범위를 정해주면 그 진위가 판별되어 명제가 된다. 예를 들어 \[ \mbox{모든 실수 \(x\)에 대하여 \(x^{2}\geq 0\)} \] 은 참인 명제이고 \[ \mbox{어떤 실수 \(x\)에 대하여 \(x^{2}=-1\)} \] 은 거짓인 명제이다.

전체집합 \(U\)에서 정의된 조건 \(p(x)\)의 진리집합을 \(P\)라고 할 때, 명제 \[ \mbox{모든 \(x\)에 대하여 \(p(x)\)} \] 는 \(P=U\)이면 참이고, \(P\neq U\)이면 거짓이다.⁴ 또한 명제 \[ \mbox{어떤 \(x\)에 대하여 \(p(x)\)} \] 는 \(P\neq\varnothing\)이면 참이고 \(P=\varnothing\)이면 거짓이다.

한정술사가 포함된 명제를 기호를 이용해 더 간단히 쓰기도 한다. 보통 명제 \[ \mbox{모든 \(x\)에 대하여 \(p(x)\)} \] 를 간단히 \[ (\forall x) (p(x)) \] 로 나타내고, 명제 \[ \mbox{어떤 \(x\)에 대하여 \(p(x)\)} \] 를 간단히 ⁵ \[ (\exists x)(p(x)) \] 로 나타낸다. 참고로 \(\forall\)은 All의 A를 거꾸로 쓴 것이고 \(\exists\)는 Exists의 E를 거꾸로 쓴 것이다.

한정기호의 부정

조건 \(p(x)\)의 진리집합이 \(P\)라고 하자. 명제 \[ \mbox{어떤 \(x\)에 대하여 \(p(x)\)} \] 의 뜻은 \(P\neq \varnothing\)과 동일하므로 이를 부정하면 \(P=\varnothing\)이다. 즉 \(P^{\mathrm{C}}=U\)라는 뜻이다. 이를 다시 표현하면 \[ U=P^{\mathrm{C}}=\{ x\mid\ \sim p(x)\} \] 이므로 명제 \[ \mbox{모든 \(x\)에 대하여 \(\sim p(x)\)} \] 로 쓸 수 있다. 따라서 다음의 두 명제 \[ \sim [\mbox{어떤 \(x\)에 대하여 \(p(x)\)}],\quad \mbox{모든 \(x\)에 대하여 \(\sim p(x)\)} \] 는 논리적으로 동치이다. 마찬가지로 다음의 두 명제 \[ \sim [\mbox{모든 \(x\)에 대하여 \(p(x)\)}],\quad \mbox{어떤 \(x\)에 대하여 \(\sim p(x)\)} \] 도 논리적으로 동치임을 알 수 있다.

유제 1.23 다음 명제의 부정을 말하여라.

1. 모든 사람은 머리가 있다.
2. 우리 반 학생은 모두 여학생이다.
3. 머리카락이 하얀 사람도 있다.
4. 해산물을 먹지 못하는 사람이 있다.
5. 휴대전화를 소유하지 않은 사람은 없다.
6. 누구나 인터넷을 할 줄 안다.

---

1. 기호 \(\equiv\)는 문자나 개념을 정의할 때에 기호 \(=\)을 대신하여 사용되기도 한다. 예를 들어 '\(f(x)\equiv x^{2}+3\)일 때 \(f(1)=4\)이다.'와 같이 쓴 것은 함수 \(f\)를 \(x^{2}+3\)으로 정의하면 \(f(1)\)은 \(4\)와 같다.’라는 뜻이다. 참고로 기호 \(:=\) 역시 문자나 기호의 뜻을 정의할 때 많이 쓰는 기호이다. 예를 들어 \(h:=a+3\)으로 쓰면 \(h\)를 \(a+3\)으로 정의한다는 뜻이다.
2. 여기서 \(c\)는 모순명제.
3. 재미삼아 \(\sqrt[3]{2}\)가 무리수인 것도 보여보아라.
4. '모든'을 '임의의'로 바꾸어 써도 같은 뜻이 된다.
5. 명제 '어떤 \(x\)에 대하여 \(p(x)\)'는 명제 '\(p(x)\)인 \(x\)가 존재한다.'와 동일한 말이다.